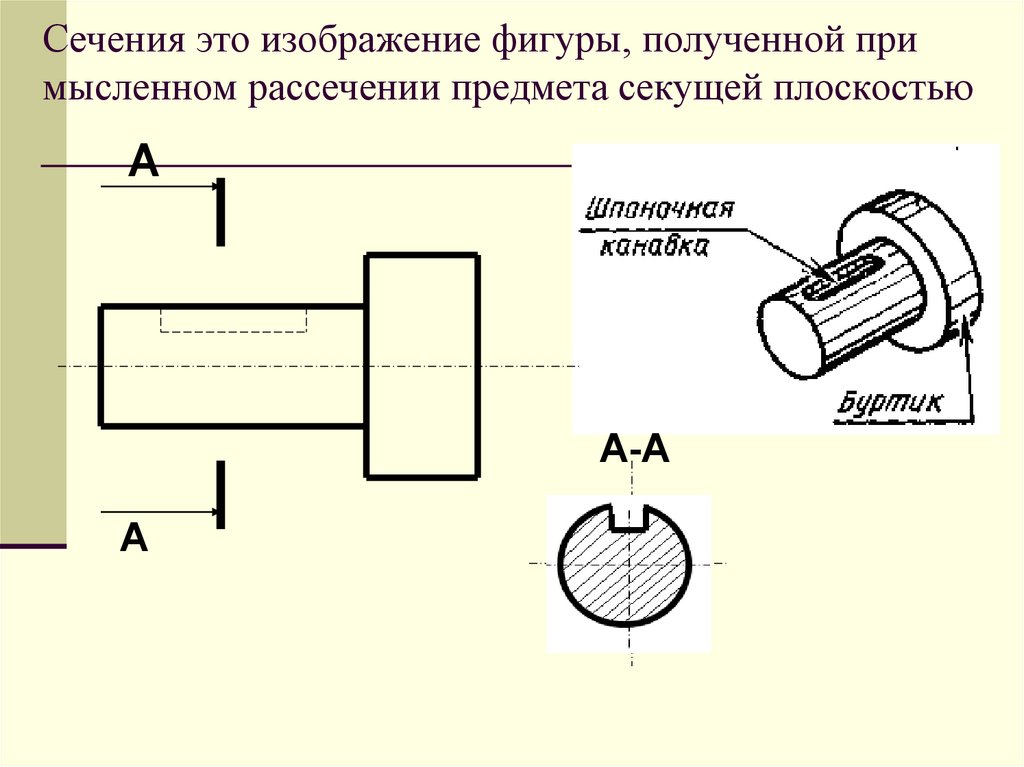
36 — сопротивление проводника • 31415.ru
Сопротивление проводника пропорционально длине и обратно пропорционально площади сечения проводника.
R — электрическое сопротивление проводника, Ом
ρ — удельное сопротивление проводника, Ом∙м
L — длина проводника, м
S — площадь сечения проводника, м2
Чем длиннее провод, тем больше его сопротивление, чем толще провод, тем его сопротивление меньше. Удобно использовать аналогию с водопроводной трубой и потоком воды. Чем толще труба, тем меньше сопротивление потоку. Чем длиннее, тем сопротивление больше.
ρ — удельное сопротивление проводника, является физическим свойством вещества. В качестве обозначения используется латинская буква — ρ, которая читается как «ро». Этой же буквой обозначается плотность веществ.
Обратите внимание! На практике, сечения проводов измеряют в — мм2(миллиметр в квадрате), но так как в системе СИ необходимо проводить вычисления площади проводника в квадратных метрах — м
Например, вот так выглядит удельное сопротивление алюминия в разных таблицах.
Алюминий — 0,027 Ом∙мм2/м
Алюминий — 2.7·10-8 Ом·м
Поэтому нужно всегда смотреть на размерность удельного сопротивления, и проверять полученный результат на соответствие реальности.
К примеру, если в задаче дано удельное сопротивление проводника 1 Oм∙мм2/м.
Значит, чтобы получить результат в Омах, нужно умножить эту величину на метры и разделить на мм2. Если взять проводник длинной 6 метров, сечением 2 мм2 и удельным сопротивлением 1 Oм∙мм2/м, то сопротивление этого проводника будет равно 3 Ома.
Таблица удельных сопротивлений металлов при 20 ° C.
| Вещество | Ом∙мм2/м |
|---|---|
| Медь | 0,017 |
| Серебро | 0,016 |
| Золото | 0,023 |
| Хром | 0,027 |
| Алюминий | 0,028 |
| Железо | 0,098 |
| Вольфрам | 0,055 |
| Свинец | 0,22 |
| Нихром | 1,1 |
| Графит | 8,0 |
Как видно из таблицы, медь является одним из лучших проводников. И поэтому используется в электрических соединениях.
И поэтому используется в электрических соединениях.
Кстати, в одной из серий «Во все тяжкие», Уолтер Уайт напоминает о применении меди, своему напарнику Джесси Пинкману.
Задача 36.
Электрическую лампу сопротивлением 240 Ом, рассчитанную на напряжение 120В, надо питать от сети напряжением 220 В. Какой длины нихромовый проводник с площадью поперечного сечения 0,55 мм
Показать ответОтвет: L=100м
| Закон ома | Fiziku5
· В различных веществах содержится различное количество электронов, а атомы, между которыми эти электроны движутся, имеют различное расположение. Поэтому сопротивление проводников электрическому току зависит от материала, из которого они изготовлены, от длины и площади поперечного сечения проводника. Если сравнить два проводника, изготовленных из одного и того же материала, то более длинный проводник имеет большее сопротивление при равных площадях поперечных сечений, а проводник с большим поперечным сечением имеет меньшее сопро-тивление при равных длинах.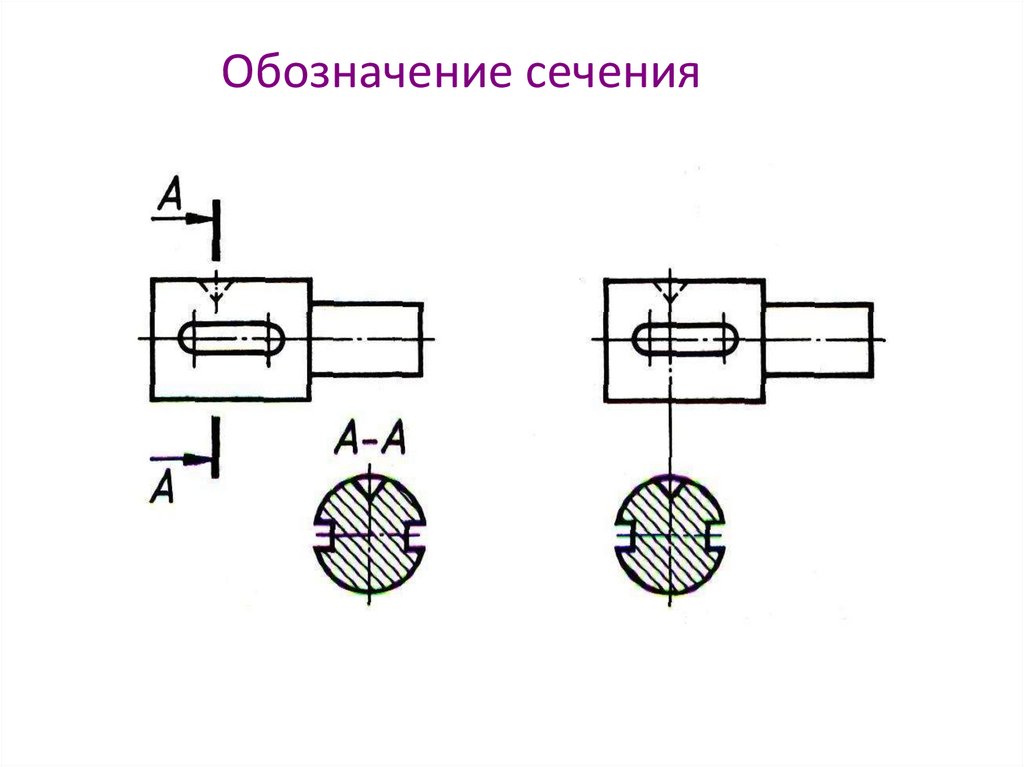
· Для оценки электрических свойств материала проводника служит удельное сопротивление — это сопротивление проводника длиной в 1 м и площадью поперечного сечения в 1 мм2. Удельное сопротивление обозначается буквой .
· Если проводник, изготовленный из материала с удельным сопротивлением , имеет длину l метров и площадь поперечного сечения q квадратных миллиметров, то сопротивление всего проводника
·
· Эта формула указывает на то, что сопротивление проводника прямо пропорционально удельному сопротивлению материала, из которого он изготовлен, а также его длине и обратно пропорционально площади поперечного сечения.
· Сопротивление проводников зависит от температуры, причем сопротивление металлических проводников с повышением температуры увеличивается. Для каждого металла существует определенный, так называемый температурный, коэффициент сопротивления, который выражает прирост сопротивления проводника при измнении температуры на 10 С отнесенный к 1

· Таким образом, температурный коэффициент сопротивления
·
· где r1 — сопротивление проводника при температуре T1,
· r2 — сопротивление того же проводника при температуре T2,
· Поясним выражение для температурного коэффициента сопротивления на примере. Положим, что медный линейный провод при температуре T1= 15° С имеет сопротивление r1 = 75 ом, а при температуре T2= 75°С r2=93 ом. Следовательно, прирост сопротивления при изменении температуры на 75—15 = 60° С составляет 93—75 = = 18 ом. Таким образом, прирост сопротивления, соответствующий изменению температуры на 1°С, равен =0,3.
· Для определения температурного коэффициента сопротивлений нужно этот прирост сопротивления отнести к 1 ом начального сопротивления, т. е. разделить на 75:
·
· Соотношение между сопротивлениями r1 и r2:
·
· Следует иметь в виду, что это соотношение справедливо при не очень высоких температурах, а для измерения сопротивлений при температурах выше 100—150° С оно не может быть использовано.
· Регулируемые сопротивления называются реостатами. Реостаты изготовляют из проволоки с большим удельным сопротивлением, например из нихрома. Сопротивление реостатов может изменяться равномерно или ступенями. Применяют также жидкостные реостаты, представляющие собой металлический сосуд, наполненный каким-либо раствором, проводящим электрический ток, например раствором соды в воде. На схемах реостаты условно обозначают так, как показано на рис. 14, б.
· Способность проводника пропускать электрический ток характеризуется проводимостью, которая представляет собой величину, обратную сопротивлению, и обозначается буквой
·
· Величина обратная удельному сопротивлению материала проводника, называется удельной проводимостью и обозначается буквой .
· Таким образом, между удельным сопротивлением и удельной проводимостью вещества имеют место следующие соотношения:
·
· Пример 1. Определить длину медной проволоки диаметром 1 мм, имеющей сопротивление 15 ом, зная, что удельное сопротивление меди 0,0175 .
Определить длину медной проволоки диаметром 1 мм, имеющей сопротивление 15 ом, зная, что удельное сопротивление меди 0,0175 .
· Решение: поперечное сечение провода равно:
·
· откуда
·
·
· Пример 2. Определить поперечное сечение нихромовой проволоки = 1 , имеющей при длине 40 м сопротивление 50 ом.
· Решение:
·
· откуда
|
·
· Пример 3. Обмотка трансформатора, изготовленная из медного провода, в нерабочем состоянии при 15° С имела сопротивление r1=2 ом. При работе сопротивление ее стало равным r2=2,48 ом. Определить температуру обмотки в рабочем состоянии, зная, что температурный коэффициент меди 0,004.
· Решение.
·
· откуда
·
· § 16. ЗАКОН ОМА
· Соотношение между э. д. с, сопротивлением и силой тока в замкнутой цепи выражается законом Ома, который может быть сформулирован так: сила тока в замкнутой цепи прямо пропорциональна электродвижущей силе и обратно пропорциональна сопротивлению всей цепи.
· Ток в цепи протекает под действием э. д. с; чем больше э. д. с. источника энергии, тем больше и сила тока в замкнутой цепи. Сопротивление цепи препятствует прохождению тока, следовательно, чем больше сопротивление цепи, тем меньше сила тока.
· Закон Ома можно выразить следующей формулой:
·
· или
·
· где r — сопротивление внешней части цепи,
· r0 — сопротивление внутренней части цепи.
Что мы подразумеваем под «поперечным сечением» в физике элементарных частиц?
Сечение рождения бозона Хиггса при столкновениях протонов при энергии центра масс 8 ТэВ.
Иногда повседневные слова кооптируются учеными и используются в качестве технических терминов. Одним из таких является слово «ягода». Разговаривая со своим другом-ботаником, я узнал, что помидоры — это ягоды, а клубника — нет — научное значение ягоды больше связано с репродуктивными структурами растения, чем с ее вкусом. Термин «поперечное сечение» — ягода физики элементарных частиц — его техническое значение сильно отличается от общепринятого.
В повседневной речи «поперечное сечение» относится к срезу объекта. Физик-физик может использовать это слово таким образом, но чаще оно используется для обозначения вероятности того, что две частицы столкнутся и отреагируют определенным образом. Например, когда физики CMS измеряют поперечное сечение «протон-протон — вершина-антивершина», они подсчитывают, сколько пар вершина-антиверхушка образовалось, когда заданное количество протонов выстрелило друг в друга.
Как физики частиц пришли к такому странному использованию термина «поперечное сечение»? Это длинная история. На заре физики элементарных частиц считалось, что частицы представляют собой крошечные неразрушимые шарики. Когда шарики или бильярдные шары катятся друг о друга, вероятность того, что они столкнутся, пропорциональна размеру шаров, если только они не нацелены точно. Субатомные частицы настолько малы, что о нацеливании отдельных частиц друг на друга не может быть и речи — лучшее, что может сделать каждый, — это выстрелить многими из них в одну и ту же общую область.
Ранние эксперименты по столкновению предназначались для измерения размера частиц по частоте их столкновений. Эксперимент Резерфорда, в котором в 1911 году столкнулись альфа-частицы и ядра золота, показал, что ядра намного меньше, чем предполагалось ранее. Но вскоре возникли несоответствия: нейтроны с большей вероятностью столкнутся с определенными ядрами, когда они движутся медленно, чем когда они быстро. Как будто нейтроны меняют площадь своего поперечного сечения в полете. Частицы, подобные нейтронам, на самом деле являются квантовыми облаками, которые проходят друг через друга или взаимодействуют с вероятностью, зависящей от энергии — вероятность столкновения имеет мало общего с твердой площадью поперечного сечения. Несмотря на то, что твердые сферы — это неверный мысленный образ, термин «поперечное сечение» прижился, и физик часто говорит, что «это поперечное сечение зависит от энергии», когда было бы бессмысленно воображать, что размер частицы действительно меняется.
Но зачем использовать «поперечное сечение», когда существуют такие альтернативы, как «вероятность» и «скорость реакции»? Поперечное сечение не зависит от интенсивности и фокуса пучков частиц, поэтому числа сечений, измеренные на одном ускорителе, можно напрямую сравнивать с числами, измеренными на другом, независимо от мощности ускорителей. Стрелы есть стрелы, сколько бы их ни было выпущено в небо.
Эта статья первоначально появилась в Fermilab Today и воспроизведена с разрешения автора.
Концепция поперечного сечения, как следует из названия, представляет собой эффективную площадь столкновения. Сечение сферической мишени
При наведении пучка частиц на мишень, значительно меньшую, чем пучок, как в эксперименте по резерфордовскому рассеянию, сечение приобретает статистический характер. Резерфорд рассчитал сечение рассеяния альфа-частиц с кинетической энергией KE на одном ядре с атомным номером Z. Сечение рассеяния на угол, больший некоторого выбранного угла, равно Для предсказания ожидаемого количества событий рассеяния выше этого угла требуется больше деталей. Когда включены сведения о луче и цели, относительная скорость рассеяния определяется как 9. Этот расчет предназначен только для расчета поперечного сечения и доли рассеяния. Обратите внимание, что применяются стандартные предположения о резерфордовском рассеянии, поэтому расчет работает только для пленок толщиной несколько микрометров или меньше. Для неуказанных параметров будут введены значения по умолчанию, но все значения, кроме поперечного сечения и доли рассеяния, можно изменить.
| Индекс Концепции Резерфорда | ||||||
| Вернуться | ||||||
Концепция поперечного сечения, как следует из названия, представляет собой эффективную площадь столкновения. В этом случае единицами поперечного сечения являются единицы площади, но для ядерного рассеяния эффективная площадь порядка площади поперечного сечения ядра. Для ядра золота с массовым числом A=197, радиус, определенный из соотношения ядерных радиусов, составляет около 7 ферми. Наиболее распространенной единицей поперечного сечения для взаимодействий ядерного рассеяния является амбар. Сечение в барнах для альфа-рассеяния выше выбранного угла является стандартной частью анализа резерфордовского рассеяния. Например, в случае альфа-частиц с энергией 6 МэВ, рассеянных на золотой фольге, вы не знаете прицельного параметра для любой данной альфа-частицы, поэтому расчет рассеянной доли принимает статистический характер. Для альфа-частиц, бомбардирующих золотую фольгу толщиной 1 микрометр, менее 1 из 100 000 соответствует условиям рассеяния на угол более 140°. Поперечное сечение рассеяния на меньшие углы будет больше, потому что альфа-каналу не нужно подходить так близко, чтобы рассеяться на меньший угол. |


 Сечение сферической мишени
Сечение сферической мишени