5.3 уклон, конусность, сопряжения
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Утверждено на заседании кафедры начертательной геометрии и черчения
21 июня 2011г.
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ –
УКЛОНЫ, КОНУСНОСТЬ, СОПРЯЖЕНИЯ
Методические указания для всех специальностей
Квалификация выпуска «Бакалавр»
Ростов-на-Дону
2011
2
Геометрические построения – уклоны, конусность, сопряжения:
Методические указания для всех специальностей. – Ростов н/Д: Рост. гос.
строит. ун-т, 2011. – 8с.
Содержат геометрические построения, необходимые для выполнения задания по инженерной графике.
Составитель: ассист. А.В. Федорова
Редактор Н.Е. Гладких Темплан 2011 г., поз. 137.
____________________________________________________________________
Подписано в печать 6.
Бумага писчая. Ризограф. Уч.-изд.л. 0,3. Тираж 20 экз. Заказ 341.
____________________________________________________________________
Редакционно – издательский центр Ростовского государственного строительного университета.
344022, Ростов – на – Дону, ул. Социалистическая, 162
Ростовский государственный строительный университет, 2011
3
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ – УКЛОНЫ, КОНУСНОСТЬ,
СОПРЯЖЕНИЯ
При изготовлении профилей прокатной стали, боковые полки выполняют так, что плоскости, ограничивающие их, не параллельны, а расположены под некоторым углом между собой.
В технике часто применяются конические детали. При вычерчивании чертежей многих деталей приходится выполнять ряд геометрических построений, и в этой связи рассмотрим следующие понятия: уклоны, конусность, сопряжения.
УКЛОНЫ
Уклон – наклон одной прямой линии к другой (рис.1).
Уклон i прямой АС определяется из прямоугольного треугольника АВС как отношение противолежащего катета ВС к прилежащему катету АС (рис.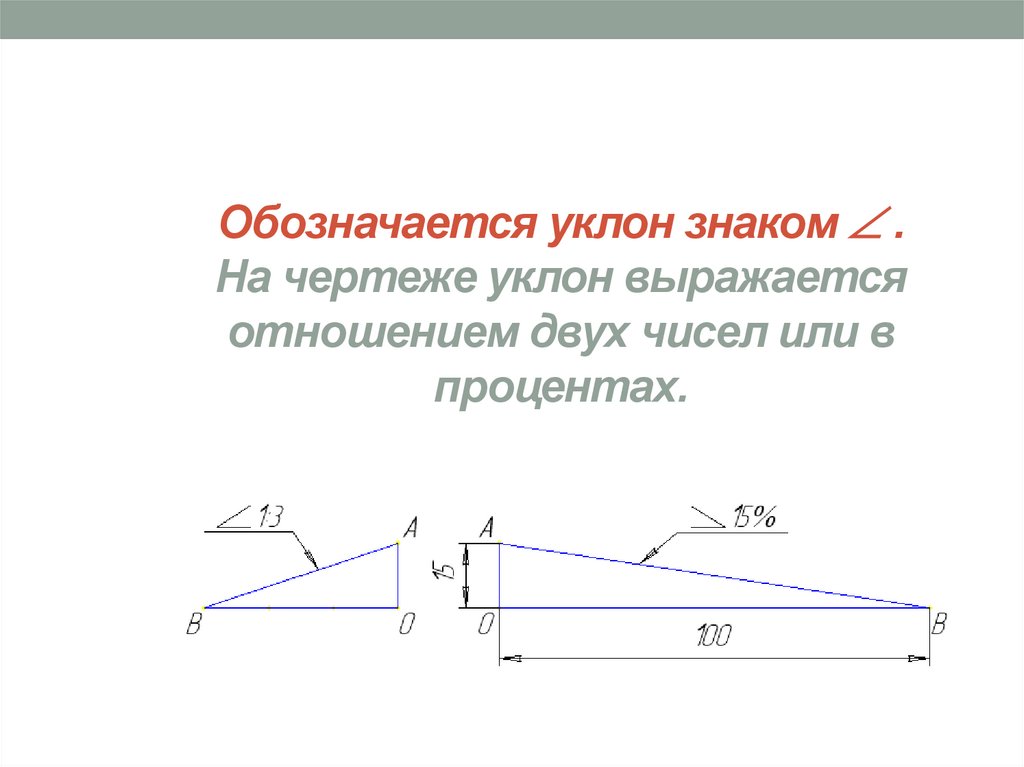
| i | h | BC | tg . |
|
| l | AC |
| ||
|
|
|
| ||
|
|
|
| i | В |
|
|
|
|
| |
1:5 | В |
|
|
| h |
|
|
|
|
| |
А | 1 С |
|
| А | С |
5 4 3 2 |
|
|
| ||
|
|
|
| ||
|
|
|
| l |
|
Рис. |
|
|
| Рис.2 |
|
Уклон может быть выражен в процентах (например, уклон в 10%
внутренних граней полок швеллера по ГОСТ 8240-89, рис. 3), отношением двух чисел (например, уклоны 1:20 и 1:4 граней рельса по ГОСТ 8168-75*) или в промилях (например, уклон 5‰ арматуры).
Знак уклона “ “, вершина которого должна быть направлена в сторону уклона, наносят перед размерным числом, располагаемым непосредственно у изображения поверхности уклона, или на полке линии – выноски, как показано на рисунках.
4
Построение уклонов
1. Провести прямую с уклоном i = 1:6 относительно прямой АЕ через точку А, лежащую на прямой АЕ (рис.3).
1
1:6 В
А 1 2 3 4 5 6 С Е
Отложим на прямой АЕ от точки А шесть произвольно выбранных единиц. Через полученную точку В восстановим перпендикуляр к АЕ длиной в одну единицу.
Рис.3
Гипотенуза АС построенного прямоугольного треугольника АВС
является искомой прямой с уклоном 1:6.
Построение полок швеллера и двутавра
На рис. 4 и 5 показано построение уклона внутренней грани верхней полки швеллера и двутавра. Построен вспомогательный треугольник ВСD с
катетами 10 и 100мм для швеллера и 12 и 100мм для двутавра.
На горизонтальном отрезке «b» отложим отрезок, равный (b-d)/2 – для швеллера и (b-d)/4 – для двутавра. Из полученной точки проведем перпендикуляр длиной t. Отложенные размеры определили положение точки К,
через которую проходит прямая с уклоном 10% для швеллера и 12% – для двутавра. Через точку К провести прямую, параллельную гипотенузе построенного треугольника.
| 10 |
|
|
d |
|
| 100 |
|
|
| |
| R |
| 1:10 |
|
|
| |
|
|
| r |
|
| t | (b-d)/2 |
|
| b |
|
|
|
| Рис. |
| 12 |
|
d |
| 100 |
| R |
|
|
| r |
t |
| (b-d)/4 |
|
| |
|
|
|
|
|
|
Рис.5
5
КОНУСНОСТЬ
Конусностью называется отношение диаметра окружности основания D
прямого конуса к его высоте h (рис.6).
КDh .
Для усеченного кругового конуса – отношение разности диаметров двух нормальных сечений конуса к расстоянию между ними (рис.7), т.е.
К | D |
| d | 2tg . |
|
|
| ||
| l |
| ||
|
|
|
|
K
2
D | . | d | D |
h |
| l |
Рис.6 | Рис.7 | |
Конусность, как и уклон, может быть выражена отношением целых чисел или в процентах. Перед размерным числом, характеризующим конусность,
наносят знак “ ”, острый угол которого должен быть направлен в сторону вершины конуса.
При одном и том же угле конусность в два раза больше уклона, так как уклон образующей конуса равен отношению радиуса его основания к высоте, а
конусность – отношению диаметра к высоте.
Таким образом, построение конусности i : n относительно данной оси сводится к построению уклонов i : 2n с каждой стороны оси.
6
СОПРЯЖЕНИЯ
Сопряжением называется плавный переход по кривой от одной линии,
прямой или кривой, к другой.
Построение сопряжений основано на свойствах прямых, касательных к окружностям, или на свойствах касающихся между собой окружностей.
Построение касательной к окружности
O
° 90
С
В
При построении прямой, касательной к
Аокружности в заданной точке С, проводят прямую перпендикулярно к радиусу ОС. При
нахождении центра окружности, касающейся заданной прямой в точке С, проводят через эту точку перпендикуляр к прямой и откладывают на нем величину радиуса заданной окружности (рис.8).
Рис.8
Построение внешней касательной к двум окружностям
Из центра О1 проводят вспомогательную окружность радиусом R3 = R1-R2
и находят точку К. Построение точки К аналогично построению точки С. Точку О1 соединяют с точкой К прямой и проводят параллельную ей прямую из точки О2 до пересечения с окружностью. Точки сопряжения С1 и С2 лежат на пересечении прямых О1К и ранее проведенной линии из центра О2 с
Точку О1 соединяют с точкой К прямой и проводят параллельную ей прямую из точки О2 до пересечения с окружностью. Точки сопряжения С1 и С2 лежат на пересечении прямых О1К и ранее проведенной линии из центра О2 с
окружностями радиусов R1 и R2 (рис. 9).
А С1
R
O
O1
С2 В
R2
O2
Рис.9
7
Сопряжение двух дуг окружностей
При внешнем касании двух окружностей расстояние между центрами О1
и О2 равно сумме радиусов R1 и R2. Точка касания С лежит на прямой,
соединяющей центры окружностей (рис.10).
При внутреннем касании окружностей О1О2 = R1 – R2. Точка касания С лежит на продолжении прямой О1О2 (рис.11).
2
R
O1 СO2
С
R1+R2
Рис.10 Рис.11
Сопряжение двух дуг окружностей дугой заданного радиуса
Из центров О1 и О2 описываются дуги вспомогательной окружности радиусом R3 = R + R1 и R4 = R + R2 (при внешнем сопряжении, рис.12)
или R3 = R – R1 и R4 = R – R2 (при внутреннем сопряжении, рис. 13). Точка О является центром искомой дуги окружности радиуса R.
13). Точка О является центром искомой дуги окружности радиуса R.
Точки сопряжения С1 и С2 будут находиться на линии центров О1О и О2О
(рис.12) или на продолжении линии центров (рис.13).
При нахождении радиуса внешне–внутреннего сопряжения вспомогательные дуги проводятся радиусами R3 = R – R1 из центра О1 и
R4 = R + R2 из центра О2 (рис.14).
Сопряжение окружности с прямой по дуге радиуса R
Из центра О1 проводится дуга радиусом R2 = R1 + R и прямая,
параллельная заданной, на расстоянии R. Пересечение вспомогательной дуги окружности и прямой определит искомый центр О. Точка сопряжения дуг С1
лежит на линии центров О1О, а прямой и дуги сопряжения С – на перпендикуляре, проведенном к заданной прямой из центра О (рис.15).
8
O2 O1
2
R4= R2 + R
R3= R1 | O |
|
Рис.12
С1
С2
R3= R – R1 |
|
O | = R – R2 |
Рис.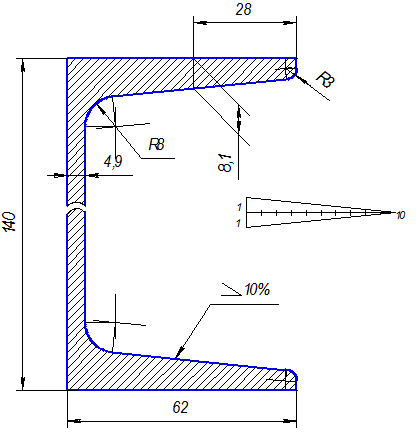 13
13
С1
O2
R3= R – R1 O
Рис.14
O1
R2= R+R1
C1
| R | O | R |
|
| ||
|
|
| |
A |
| C | B |
Рис.15
⇐ Предыдущая567891011121314Следующая ⇒ Уклоны. ГОСТ 8908-81 Уклон –это величина, характеризующая наклон одной линии (плоскости) по отношению к другой, i = tg a = ВС/АВ. Для обозначения уклонов на чертеже применяется знак (рис1) по ГОСТ 2.304-81 (размеры знака даны для шрифта № 5). Знак наносится перед размерным числом, острый угол знака должен быть направлен в сторону уклона (рис 2) Построение уклона. На рисунке в качестве примера построен профиль несимметричного двутавра, правая полка которого имеет уклон 1: 16. Для ее построения находят точку А с помощью заданных размеров 26 и 10. В стороне строят линию с уклоном 1: 16, для чего по вертикали откладывают, например, 5 мм, а по горизонтали 80 мм; проводят гипотенузу, направление которой определяет искомый уклон. С помощью рейсшины и угольника через точку А проводят линию уклона, параллельную гипотенузе. Конусности. Конусность – это отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними (рис. 1.4). C = (D – d) / L = 2 tg a / 2. Для обозначения конусности на чертеже применяется знак (рис. 1.5) по ГОСТ 2.304-81 (размеры знака даны для шрифта № 5). Знак наносится перед размерным числом, характеризующим конусность, острый угол знака должен быть направлен в сторону вершины конуса (рис. 1.6). Если нужно построить конусность 1: n относительно заданной оси, то строим уклоны 1: 2n с каждой стороны оси. K = 2i. Также построение конусности при заданной длине L и диаметре D одного из оснований можно выполнить графически следующим образом: построить на заданной оси вспомогательный полный конус, у которого произвольно взятое основание а укладывается в высоте столько раз, сколько задано в обозначении конуса.
Презентация по теме: «Лекальные и коробовые кривые» 1) Рассмотреть построение лекальных кривых: параболы, гиперболы, синусоиды. 2) Рассмотреть построение коробовых кривых: овала по заданным осям АВ и CD и овоидальной кривой. 3) Создать презентацию «Лекальные и коробовые кривые» ⇐ Предыдущая567891011121314Следующая ⇒
|
Построение линии с использованием наклона и точки
Результаты обучения
- Начертить график линии с использованием наклона и точки на линии
- Напишите уравнение прямой, используя наклон и точку пересечения с осью Y
При построении графика мы нашли один метод, который мы могли бы использовать, это составить таблицу значений.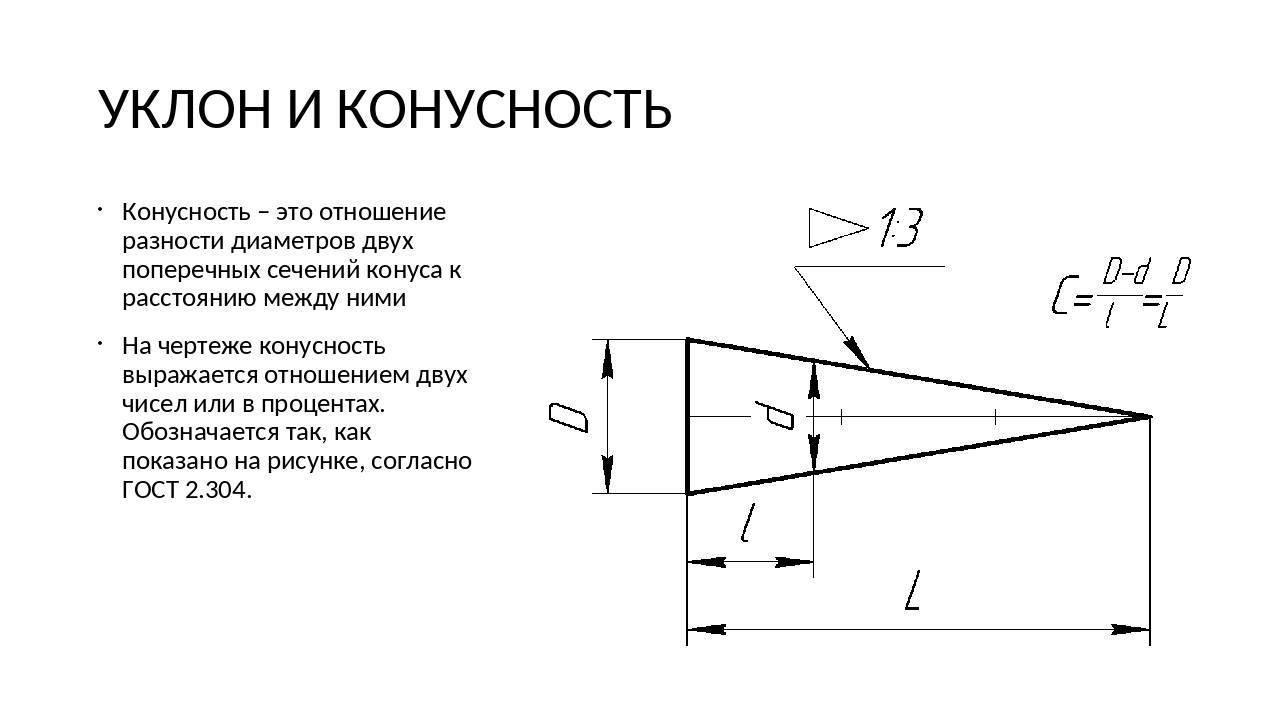 Мы также научились строить линии, нанося точки, используя точки пересечения и распознавая горизонтальные и вертикальные линии. Однако, если мы сможем определить некоторые свойства линии, мы сможем построить график намного быстрее и проще.
Мы также научились строить линии, нанося точки, используя точки пересечения и распознавая горизонтальные и вертикальные линии. Однако, если мы сможем определить некоторые свойства линии, мы сможем построить график намного быстрее и проще.
Построение линии с использованием наклона и точки на линии
Другой метод, который мы можем использовать для построения линий, — метод точка-наклон. Иногда нам будет дана одна точка и наклон линии вместо ее уравнения. Когда это происходит, мы используем определение наклона, чтобы нарисовать график линии.
пример
Нарисуйте линию, проходящую через точку [латекс]\влево(1,-1\вправо)[/латекс], наклон которой равен [латекс]м=\Большой\фрак{3}{4}[/латекс ].
Решение
Постройте заданную точку, [латекс]\влево(1,-1\вправо)[/латекс].
Используйте формулу уклона [latex]m=\Large\frac{\text{подъем}}{\text{пробег}}[/latex], чтобы определить подъем и уклон.
[латекс]\begin{array}{}\\ \\ m=\frac{3}{4}\hfill \\ \frac{\text{rise}}{\text{run}}=\frac{ 3}{4}\hfill \\ \\ \\ \text{rise}=3\hfill \\ \text{run}=4\hfill \end{array}[/latex]
Начиная с точки, которую мы начертили , отсчитываем подъем и бегом отмечаем вторую точку.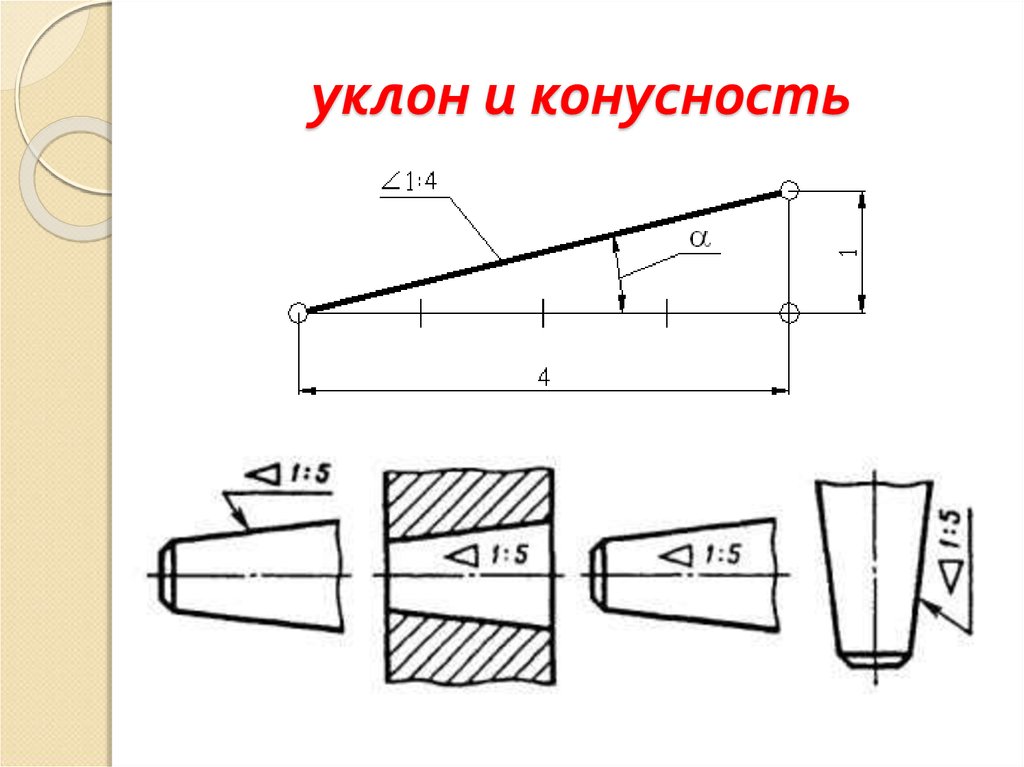 Мы считаем [латекс]3[/латекс] единицы вверх и [латекс]4[/латекс] единицы вправо.
Мы считаем [латекс]3[/латекс] единицы вверх и [латекс]4[/латекс] единицы вправо.
Затем мы соединяем точки линией и рисуем стрелки на концах, чтобы показать, что она продолжается.
Мы можем проверить нашу линию, начав с любой точки и считая вверх [латекс]3[/латекс] и вправо [латекс]4[/латекс]. Мы должны добраться до другой точки на линии.
попробуй
Нарисуй линию по заданной точке и наклону
- Постройте заданную точку.
- Используйте формулу уклона, чтобы определить подъем и уклон.
- Стартовав в заданной точке, отсчитайте подъем и бегите, чтобы отметить вторую точку.
- Соедините точки линией.
пример
Нарисуйте линию, проходящую через точку [латекс]\влево(-1,-3\вправо)[/латекс], наклон которой равен [латекс]m=4[/латекс]
Показать решение
попробуйте
Вы можете посмотреть видео ниже, чтобы увидеть еще один пример того, как построить линию с заданной точкой и наклоном.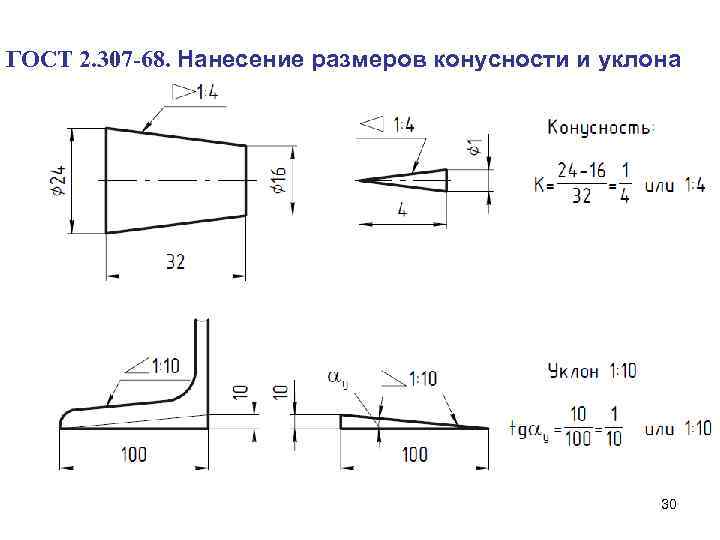
Особым случаем построения графика с использованием метода точка-наклон является ситуация, когда данная точка является точкой пересечения с осью y. Мы приведем здесь несколько примеров, а затем покажем ниже, почему этот случай так важен.
пример
Нарисуйте линию с [латекс]y[/латекс] – точка пересечения [латекс]\влево(0,2\вправо)[/латекс] и наклоном [латекс]м=-\большой\фрак{2} {3}[/latex]
Показать решение
попробуйте
Форма пересечения наклона
Теперь мы покажем вам, что особенного в случае, когда данная точка является точкой пересечения с осью Y. Наклон может быть представлен как m, а точка пересечения y , где он пересекает ось и [latex]x=0[/latex], может быть представлена как [latex](0,b)[/latex], где b — это значение, при котором график пересекает вертикальную ось y . Любая другая точка на линии может быть представлена как [латекс](х,у)[/латекс].
Любая другая точка на линии может быть представлена как [латекс](х,у)[/латекс].
Форма пересечения наклона линейного уравнения
В уравнении [latex]y=mx+b[/latex]
- m — наклон графика.
- b — это значение y точки пересечения графика с осью y.
Эта формула известна как уравнение пересечения наклона. Если мы знаем наклон и точку пересечения y , мы можем легко найти уравнение, представляющее линию.
Мы также можем легко найти уравнение, взглянув на график и найдя наклон и y -пересечение.
Мы можем двигаться и в обратном направлении. Когда нам дается уравнение в форме наклона-пересечения [латекс]y=mx+b[/латекс], мы можем легко определить наклон и y -пересечение и построить уравнение на основе этой информации. Когда у нас есть уравнение в форме пересечения наклона, мы можем изобразить его, сначала построив точку пересечения по оси y, а затем, используя наклон, найдем вторую точку и соединим точки.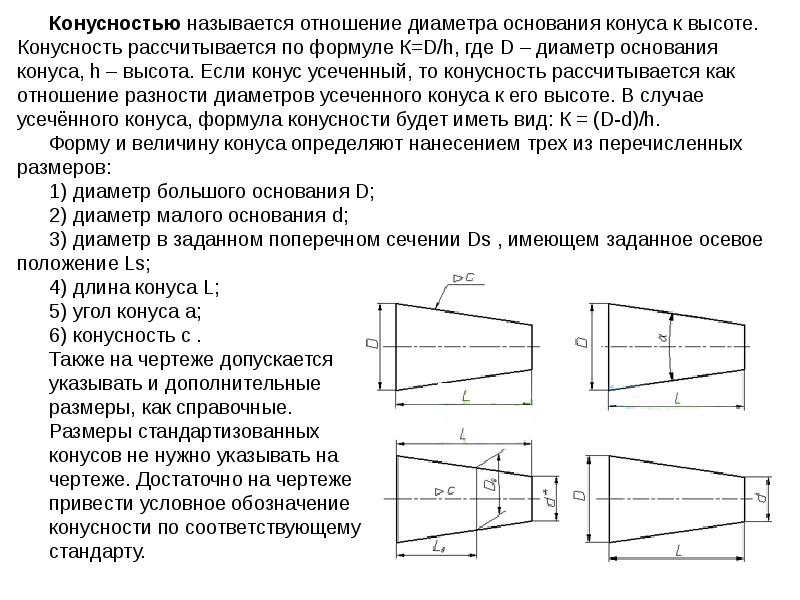
(ПРИМЕЧАНИЕ: важно, чтобы уравнение сначала было в форме пересечения наклона. Если это не так, нам придется решить его для [латекс]y[/латекс], чтобы мы могли определить наклон и [латекс] y[/latex]-intercept.)
Попробуйте
Вы можете посмотреть видео ниже, чтобы увидеть еще один пример того, как написать уравнение линии, когда задан график, определяя наклон и y-пересечение.
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Как найти наклон по графику? Примеры
В процессе определения уклона по графику используется формула уклона подъем/спуск. Когда дан график линии и нас просят найти ее уравнение, первое, что нам нужно сделать, это найти ее наклон.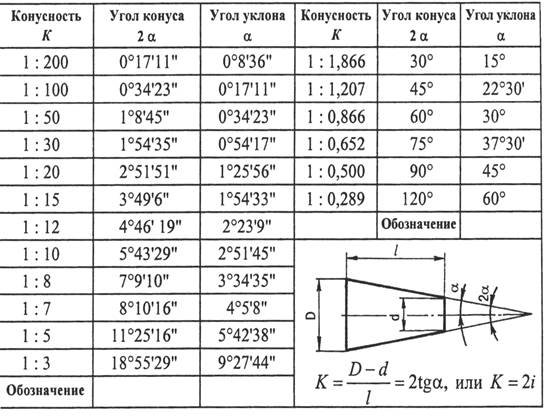 Мы можем выбрать любые две точки (x₁, y₁) и (x₂, y₂) на линии и использовать формулу (y₂ – y₁) / (x₂ – x₁) для расчета наклона по графику.
Мы можем выбрать любые две точки (x₁, y₁) и (x₂, y₂) на линии и использовать формулу (y₂ – y₁) / (x₂ – x₁) для расчета наклона по графику.
Давайте посмотрим на другие способы расчета наклона по графику, а также на другие примеры. Давайте также узнаем, как найти наклон горизонтальных и вертикальных линий.
| 1. | Определение наклона по графику |
| 2. | Расчет уклона по графику с использованием формулы уклона |
| 3. | Нахождение наклона горизонтальной линии на графике |
| 4. | Нахождение наклона вертикальной линии на графике |
| 5. | Часто задаваемые вопросы о том, как найти уклон на графике |
Определение наклона по графику
Наклон линии — это отношение подъема к длине. Следовательно, вот шаги, чтобы найти наклон по графику.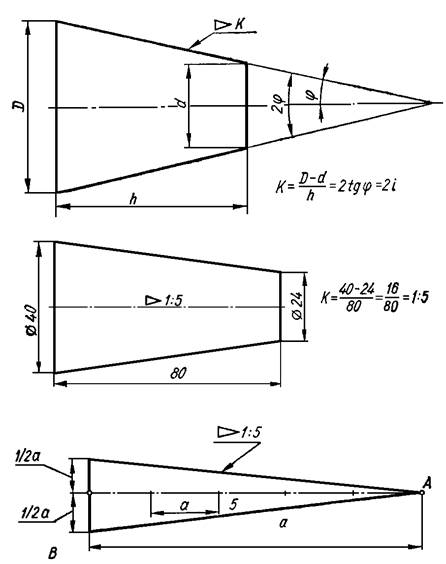
- Выберите любые две случайные точки на графике линии (желательно с целочисленными координатами).
- Обозначьте их как A и B (в любом порядке).
- Рассчитать “подъем” от А до Б. Идя по вертикали от А до Б, если нам нужно пройти
«вверх», то подъем положительный;
«вниз», то рост отрицательный. - Рассчитать “пробег” от А до Б. При горизонтальном движении от А до Б, если нам нужно идти
«правильно», то пробег положительный;
“влево”, то пробег отрицательный. - Теперь используйте формулу: уклон = подъем/спуск.
Вот пример графика линии.
Здесь мы взяли A = (1, 1) и B = (0, 3). Обратите внимание, что здесь мы взяли точки с целочисленными координатами. Составьте прямоугольный треугольник, начинающийся в точке А и заканчивающийся в точке В, что облегчит процесс поиска подъема и бега. Здесь мы должны двигаться вертикально «вверх», чтобы добраться до B из A и, следовательно, подняться = +2; и мы должны двигаться горизонтально «влево», чтобы добраться от A до B и, следовательно, запустить = -1.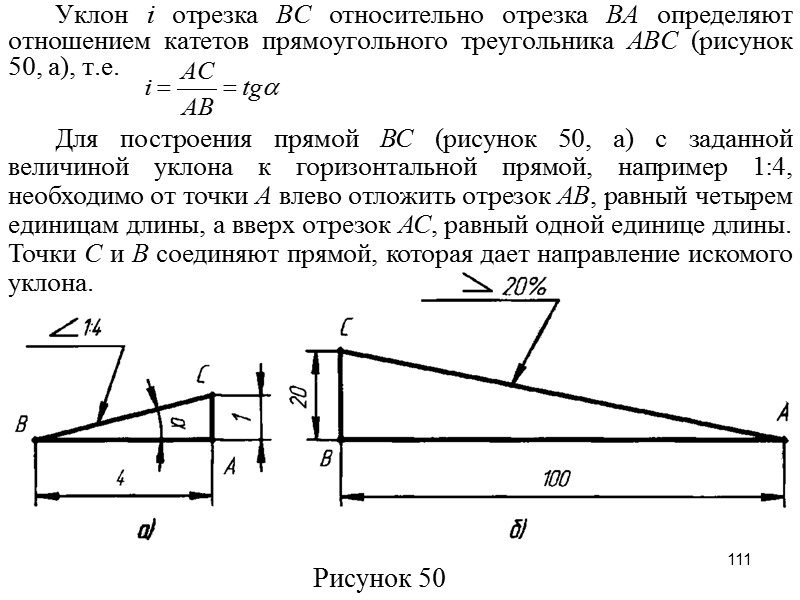 Итак, наклон = подъем/бег = 2/-1= -2.
Итак, наклон = подъем/бег = 2/-1= -2.
Нам не нужно выбирать эти точки только для расчета наклона, а также нам не нужно выбирать их в указанном выше порядке. Здесь вы можете увидеть график той же линии, где одни и те же точки выбраны в разном порядке и выбраны разные точки. Обратите внимание, что наклон линии (окончательный ответ) будет в конечном итоге одинаковым.
Расчет уклона по графику с использованием формулы уклона
Формула наклона используется для определения наклона линии, соединяющей две точки (x₁, y₁) и (x₂, y₂). Используя эту формулу, наклон линии составляет m = (y₂ – y₁) / (x₂ – x₁). Мы можем использовать ту же формулу, чтобы найти наклон линии по ее графику. Для этого:
- Выберите любые две точки на графике.
- Представьте их как (x₁, y₁) и (x₂, y₂) в любом порядке.
- Примените формулу m = (y₂ – y₁) / (x₂ – x₁), чтобы найти наклон.
Пример: Рассмотрим приведенные выше графики.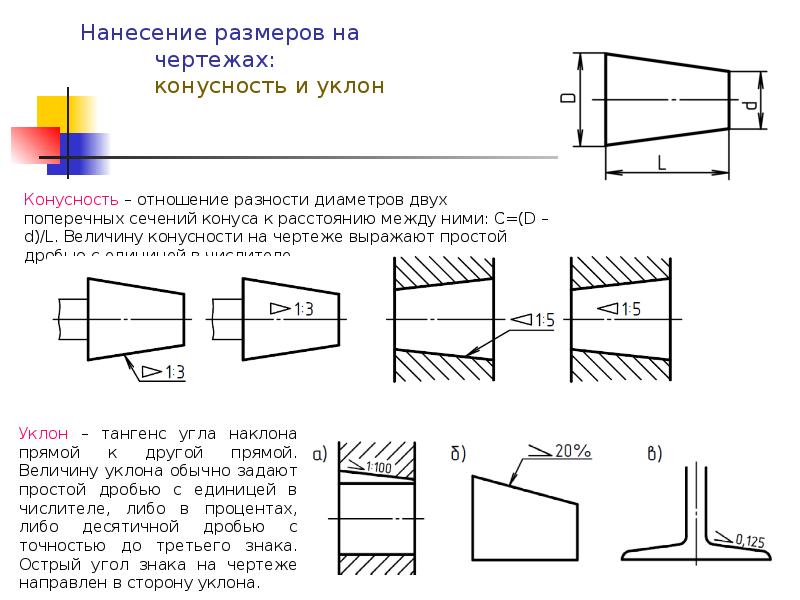 Выберем на нем две точки (-1, 5) и (1, 1). Теперь пусть
Выберем на нем две точки (-1, 5) и (1, 1). Теперь пусть
- (x₁, y₁) = (-1, 5)
- (х₂, у₂) = (1, 1)
Уклон, м = (y₂ – y₁) / (x₂ – x₁)
= (1 – 5) / (1 – (-1))
= -4/2
= -2
Мы получили тот же наклон (-2), когда вычисляли наклон также с использованием подъема/спуска.
Нахождение наклона горизонтальной линии на графике
Горизонтальная линия — это линия, параллельная оси x. Таким образом, все точки на горизонтальной линии имеют одинаковые координаты y. Таким образом, для любых двух точек на горизонтальной линии подъем = 0. Следовательно, наклон = подъем/набег = 0/набег = 0. Следовательно, наклон горизонтальной линии всегда равен 0. Вот пример.
Здесь наклон горизонтальной линии y = 3 рассчитывается с использованием обоих методов подъем/спуск и (y₂ – y₁) / (x₂ – x₁). Вы можете заметить, что наклон в обоих случаях равен 0,
Определение наклона вертикальной линии по графику
Вертикальная линия всегда параллельна оси Y. Таким образом, все точки на вертикальной линии имеют одинаковые x-координаты. Таким образом, для любых двух точек на нем пробег = 0. Следовательно, наклон = подъем/пробег = подъем/0 = не определено. Следовательно, наклон вертикальной линии всегда не определен. Вот пример.
Таким образом, все точки на вертикальной линии имеют одинаковые x-координаты. Таким образом, для любых двух точек на нем пробег = 0. Следовательно, наклон = подъем/пробег = подъем/0 = не определено. Следовательно, наклон вертикальной линии всегда не определен. Вот пример.
Здесь наклон вертикальной линии x = 3 рассчитывается по обеим формулам подъем/спуск и (y₂ – y₁) / (x₂ – x₁). Вы можете заметить, что наклон в обоих случаях не определен.
Важные примечания по нахождению наклона на графике
- Наклон на графике можно рассчитать, выбрав любые две точки на нем и применив формулу подъем/спуск.
- Его также можно найти, выбрав две точки и применив формулу (y₂ – y₁) / (x₂ – x₁).
- Наклон горизонтальной линии всегда равен 0.
- Наклон вертикальной линии всегда не определен.
☛ Связанные темы:
- Калькулятор формы уклона точки
- Калькулятор определения уклона по двум точкам
- Калькулятор формы пересечения уклона
- Уравнение линейного калькулятора
Часто задаваемые вопросы о том, как найти уклон на графике
Как найти уклон на графике?
Чтобы найти наклон по графику , найдите на нем любые две точки.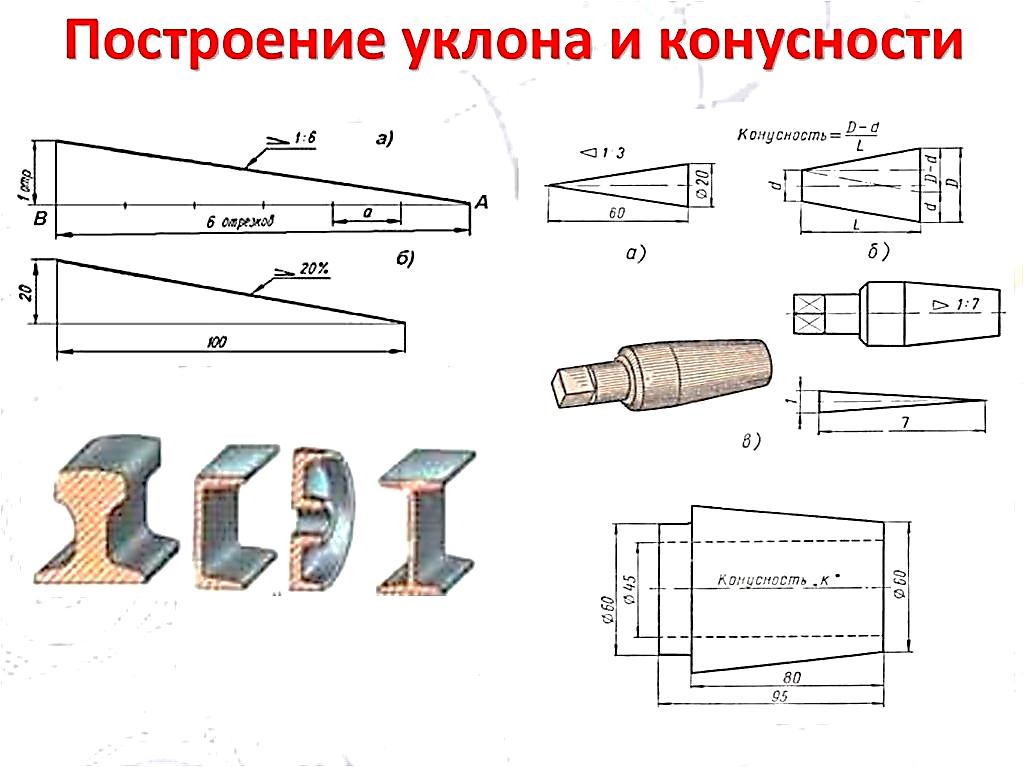 Предпочтительно выбрать нижнюю точку как A, а верхнюю точку как B. Посмотрите, насколько нам нужно «подняться» и «пробежать», чтобы перейти от A к B. Тогда отношение подъем/пробег даст нам наклон (градиент). Обратите внимание на следующее при расчете подъема и пробега:
Предпочтительно выбрать нижнюю точку как A, а верхнюю точку как B. Посмотрите, насколько нам нужно «подняться» и «пробежать», чтобы перейти от A к B. Тогда отношение подъем/пробег даст нам наклон (градиент). Обратите внимание на следующее при расчете подъема и пробега:
- подъем положителен, если вы поднимаетесь из пункта А в пункт В; это отрицательно, если вы идете вниз. Прогон
- положительный, если вы идете прямо из А в Б; это отрицательно, если вы идете налево.
Как рассчитать наклон горизонтальной линии на графике?
Мы используем формулу подъем/спуск для расчета наклона по графику . Для любых двух точек на горизонтальной линии подъем всегда равен 0. Таким образом, его наклон равен 0/run = 0. Таким образом, наклон горизонтальной линии всегда равен 0, и мы можем сказать это, не вычисляя его.
Как найти наклон на графике, используя формулу наклона?
Формула наклона (градиента) говорит, что наклон линии с двумя точками на ней (x₁, y₁) и (x₂, y₂) равен m = (y₂ – y₁) / (x₂ – x₁).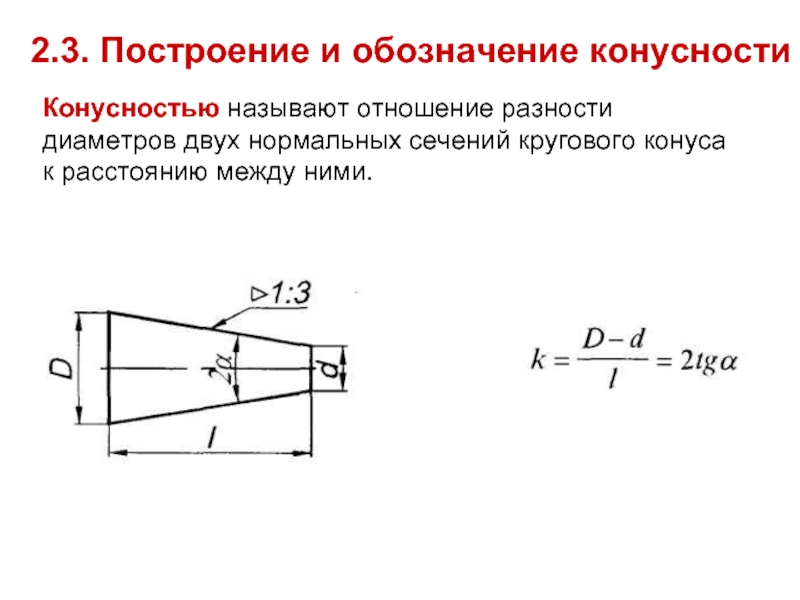

 1
1 4
4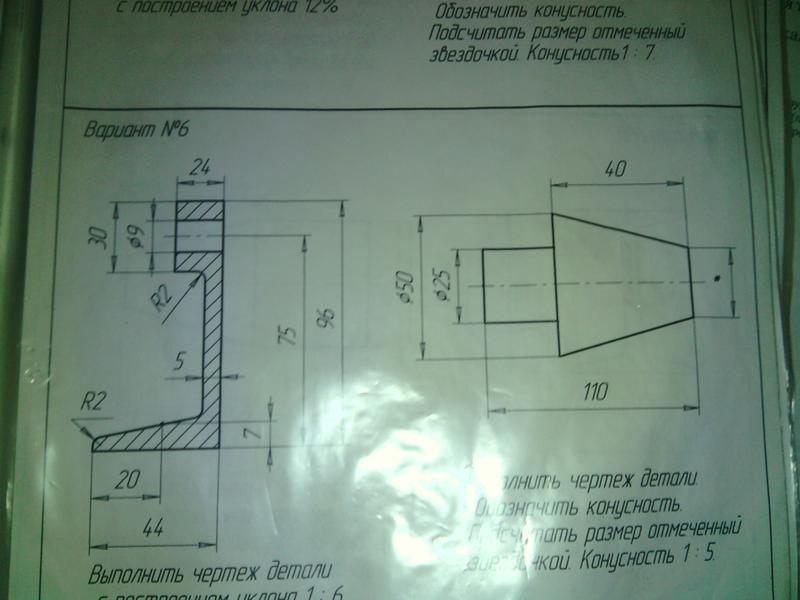
 На примере (рисунок) наглядно продемонстрировано построение уклона. Для построения уклона 1: 1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1: 2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
На примере (рисунок) наглядно продемонстрировано построение уклона. Для построения уклона 1: 1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1: 2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а. ГОСТ 8593-81
ГОСТ 8593-81 Затем провести образующие искомого конуса параллельно образующим вспомогательного конуса через концы заданного диаметра D, как показано на рисунке.
Затем провести образующие искомого конуса параллельно образующим вспомогательного конуса через концы заданного диаметра D, как показано на рисунке. Для этого все десять пальцев разбиваются на пять пар…
Для этого все десять пальцев разбиваются на пять пар…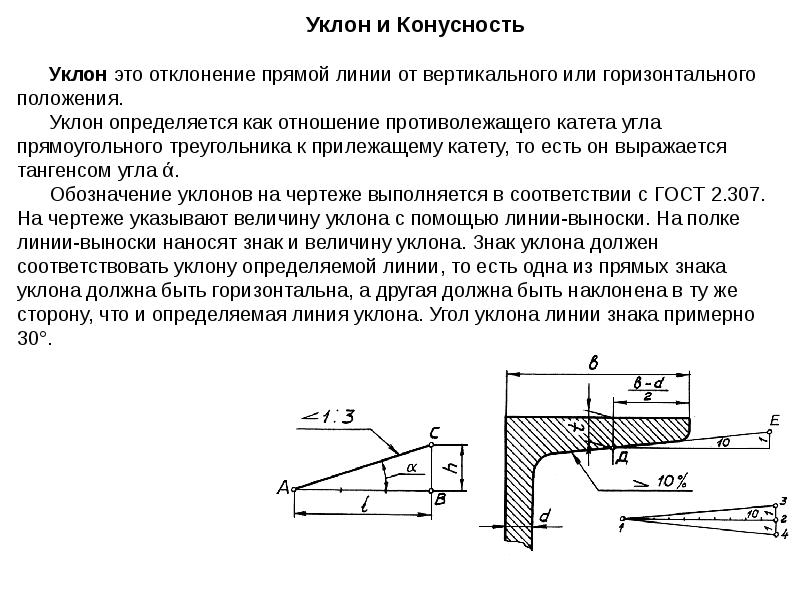 ..
..