Сечения многогранников – Геометрия – Презентации
СЕЧЕНИЯ МНОГОГРАННИКОВ
Если многогранник лежит по одну сторону от данной плоскости, то он может: а) не иметь с плоскостью ни одной общей точки; б) иметь одну общую точку – вершину многогранника; в) иметь общий отрезок – ребро многогранника; г) иметь общий многоугольник – грань многогранника.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Если у многогранника имеются точки, лежащие по разные стороны от данной плоскости, то общ ая часть многогранника и плоскости называе тся сечением многогранника плоскостью .
Диагональные сечения
Сечение призмы плоскостью, проходящей через диагональ основания и два прилежащих к ней боковых ребра, называется диагональным сечением призмы.
Сечение пирамиды плоскостью, проходящей через диагональ основания и вершину, называется диагональным сечением пирамиды.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Пусть плоскость пересекает пирамиду и параллельна ее основанию.
Часть пирамиды, заключенная между этой плоскостью и основанием, называется усеченной пирамидой. Сечение пирамиды также называется основанием усеченной пирамиды.
Упражнение 1
Какой фигурой может быть сечение многогранника плоскостью?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: Многоугольником или объединением нескольких многоугольников.
Упражнение 2
Сколько диагональных сечений имеет n -угольная: а) призма; б) пирамида?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: а) ;
б) .
4
Упражнение 3
Может ли в сечении куба плоскостью получиться:
а) треугольник ?
б) правильный треугольник ?
в) равнобедренный треугольник ?
г) прямоугольный треугольник ?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
д) тупоугольный треугольник ?
Ответ: а) Да;
в) да;
г) нет;
д) нет.
б) да;
Упражнение 4
Может ли в сечении куба плоскостью получиться:
а) квадрат;
б) прямоугольник;
в) параллелограмм;
г) ромб;
д) трапеция;
е) прямоугольная трапеция?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: а) Да;
б) да;
в) да;
е) нет.
г) да;
д) да;
6
Упражнение 5
Может ли в сечении куба плоскостью получиться:
а) пятиугольник;
б) правильный пятиугольник?
Ответ: а) Да;
б) нет. У пятиугольников, которые получаются в сечении куба, имеются две пары параллельных сторон, а у правильного пятиугольника таких сторон нет.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Упражнение 6
Может ли в сечении куба плоскостью получиться:
а) шестиугольник;
б) правильный шестиугольник;
в) многоугольник с числом сторон больше шести?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: а) Да;
в) нет.
б) да;
Упражнение 7
Может ли в сечении правильного тетраэдра плоскостью получиться : а) остроугольный треугольник; б) прямоугольный треугольник; в) тупоугольный треугольник ?
Ответ: а) да;
б) да. Пусть ABCD – единичный тетраэдр. Точка E на ребре AD отстоит от вершины A на расстояние ¼ . Точка F на ребре AB отстоит от вершины A на расстояние x . Найдем x , для которого угол CEF будет прямым.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
По теореме косинусов находим CE 2 = 13/16, CF 2 = x 2 + 1 – x , EF 2 = 1/16 + x 2 – x /4. Используя теорему Пифагора находим x = 1/6.
в) да. Если точку G на ребре AB взять между A и F , то угол CEF будет тупой.
9
Упражнение 8
Может ли в сечении правильного тетраэдра плоскостью получиться квадрат?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: Да.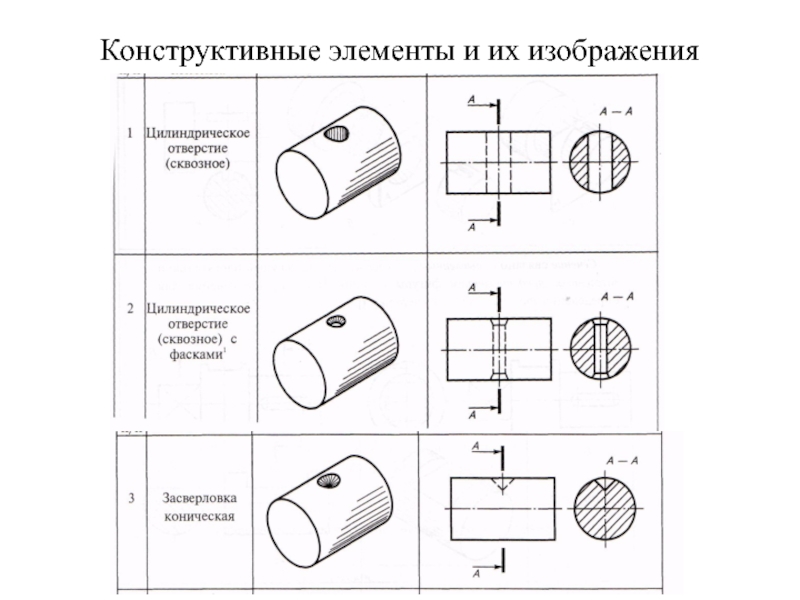
Если сечение проходит через середины ребер.
Упражнение 9
Может ли в сечении тетраэдра плоскостью получиться четырехугольник, изображенный на рисунке ?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: Нет.
Упражнение 10
Какие многоугольники можно получить в сечении четырехугольной пирамиды плоскостью?
Ответ: Треугольник, четырехугольник, пятиугольник.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Упражнение 11
Может ли в сечении октаэдра плоскостью получиться:
а) треугольник;
б) четырехугольник;
в) пятиугольник;
г) шестиугольник;
д) семиугольник;
е) восьмиугольник?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: а) Нет;
б) да;
в) нет;
г) да;
д) нет;
е) нет.
Построение сечений
При построении сечений многогранников, базовыми являются построения точки пересечения прямой и плоскости, а также линии пересечения двух плоскостей.
Если даны две точки A и B прямой и известны их проекции A’ и B’ на плоскость, то точкой С пересечения данных прямой и плоскости будет точка пересечения прямых AB и A’B’
Если даны три точки A , B , C плоскости и известны их проекции A’ , B’ , C’ на другую плоскость, то для нахождения линии пересечения этих плоскостей находят точки P и Q пересечения прямых AB и AC со второй плоскостью. Прямая PQ будет искомой линией пересечения плоскостей.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Упражнение 1
Постройте сечение куба плоскостью, проходящей через точки
Решение. Для построения сечения куба, проходящего через точки E , F и вершину B ,
Соединим отрезками точки E и B , F и B .
Через точки E и F проведем прямые, параллельные BF и BE , соответственно.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Полученный параллелограмм BFGE будет искомым сечением.
Упражнение 2
Постройте сечение куба плоскостью, проходящей через точки E , F , G , лежащие на ребрах куба .
Решение. Для построения сечения куба, проходящего через точки E , F , G ,
проведем прямую EF и обозначим P
её точку пересечения с AD .Обозначим Q точку пересечения прямых PG и AB .
Соединим точки E и Q , F и G .
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Полученная трапеция EFGQ будет искомым сечением.
Упражнение 3
Постройте сечение куба плоскостью, проходящей через точки E , F , G , лежащие на ребрах куба .
Решение. Для построения сечения куба, проходящего через точки E , F , G ,
проведем прямую EF и обозначим P её точку пересечения с AD .
Обозначим Q , R точки пересечения прямой PG с AB и DC .
В режиме слайдов построение производится по шагам, кликаньем мышкой.
Обозначим S точку пересечения FR c СС 1 .
Соединим точки E и Q , G и S .
Полученный пятиугольник EFSGQ будет искомым сечением.
Упражнение 4
Постройте сечение куба плоскостью, проходящей через точки E , F , G , лежащие на ребрах куба .
Решение. Для построения сечения куба, проходящего через точки E , F , G ,
найдем точку P пересечения прямой EF и плоскости грани ABCD .
Обозначим Q , R точки пересечения прямой PG с AB и CD .
В режиме слайдов построение производится по шагам, кликаньем мышкой.
Проведем прямую RF и обозна – чим S , T её точки пересечения с CC 1 и DD 1 .
Проведем прямую TE и обозначим U её точку пересечения с A 1 D 1 .
Соединим точки E и Q , G и S , U и F .
Полученный шестиугольник EUFSGQ будет искомым сечением.
Упражнение 5
Постройте сечение куба плоскостью, проходящей через точки E , F , G , принадлежащие граням BB 1 C 1 C , CC 1 D 1 D , AA 1 B 1 B , соответственно.
Решение. Из данных точек опустим перпендикуляры EE’ , FF’ , GG’ на плоскость грани ABCD , и найдем точки I и H пересечения прямых FE и FG с этой плоскостью.
IH будет линией пересечения искомой плоскости и плоскости грани ABCD . Обозначим
В режиме слайдов построение производится по шагам, кликаньем мышкой.
Проведем прямые PG и QE и обозначим R , S их точки пересечения с AA 1 и CC 1 .
Проведем прямые SU , UV и RV , параллельные PR , PQ и QS .
Полученный шестиугольник RPQSUV будет искомым сечением.
Упражнение 6
Постройте сечение куба плоскостью, проходящей через точки E , F , лежащие на ребрах куба , параллельно диагонали BD .
Решение. Проведем прямые FG и EH , параллельные BD .
Проведем прямую FP , параллельную EG , и соединим точки P и G .
Соединим точки E и G , F и H .
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Полученный пятиугольник EGPFH будет искомым сечением .
20
Постройте сечение двух кубов плоскостью, проходящей через точки K , L , M , лежащие на ребрах куба .
Упражнение 7
Решение. Сначала построим сечение верхнего куба. Это будет шестиугольник LNMPKQ.
Продолжим MN , PK и QL. Соответствующие точки обозначим R , S и U , V .
Проведем прямые RX и VY , параллельные UV и SR , соответственно.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Искомое сечение состоит из двух шестиугольников LNMPKQ и RSUVYX.
Постройте сечение призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки E , F , G .
Упражнение 8
Решение.
Соединим точки E и F .
Проведем прямую FG и ее точку пересечения с CC 1 обозначим H .
Проведем прямую EH и ее точку пересечения с A 1 C 1 обозначим I .
Соединим точки I и G .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Полученный четырехугольник EFGI будет искомым сечением .
Постройте сечение призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки E , F , G .
Упражнение 9
Решение. Проведем прямую EG и обозначим H и I ее точки пересечения с CC 1 и AC .
Проведем прямую IF и ее точку пересечения с AB обозначим K .
Проведем прямую FH и ее точку пересечения с B 1 C 1 обозначим L .
Соединим точки E и K , G и L .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Полученный пятиугольник EKFLG будет искомым сечением .
Постройте сечение призмы ABCA 1 B 1 C 1 плоскостью, параллельной AC 1 , проходящей через точки D и D 1 .
Упражнение 1 0
Решение. Через точку D проведем прямую параллельную AC 1 и обозначим E ее точку пересечения с прямой BC 1 . Эта точка будет принадлежать плоскости грани ADD 1 A 1 .
Проведем прямую DE и обозначим F ее точку пересечения с ребром BC .
Соединим отрезком точки F и D .
Через точку D проведем прямую параллельную прямой FD и обозначим G точку ее пересечения с ребром A 1 C 1 , H – точку ее пересечения с прямой A 1 B 1 .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Проведем прямую DH и обозначим P ее точку пересечения с ребром AA 1 .
Соединим отрезком точки P и G .
Полученный четырехугольник EFIK будет искомым сечением .
Построить сечение призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки E на ребре BC , F на грани ABB 1 A 1 и G на грани ACC 1 A 1 .
Упражнение 1 1
Решение. Проведем прямую GF и найдем точку H ее пересечения с плоскостью ABC .
Проведем прямую EH , и обозначим P и I ее точки пересечения с AC и AB .
Проведем прямые PG и IF , и обозначим S , R и Q их точки пересечения с A 1 C 1 , A 1 B 1 и BB 1 .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Соединим точки E и Q , S и R .
Полученный пятиугольник EQRSP будет искомым сечением .
Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки A , B , D 1 .
Упражнение 1 2
Решение. Заметим, что сечение будет проходить через точку E 1.
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Проведем прямую AB и найдем ее точки пересечения K и L с прямыми CD и FE .
Проведем прямые KD 1 , LE 1 и найдем их точки пересечения P , Q с прямыми CC 1 и FF 1 .
Шестиугольник ABPD 1 E 1 Q будет искомым сечением .
Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки A , B’ , F’ .
Упражнение 1 3
Решение. Проведем отрезки AB’ и AF’ .
Через точку B’ проведем прямую, параллельную AF’ , и ее точку пересечения с EE 1 обозначим E’ .
Через точку F’ проведем прямую, параллельную AB’ , и ее точку пересечения с CC 1 обозначим C’ .
Через точки E’ и C’ проведем прямые, параллельные AB’ и AF’ , и их точки пересечения с D 1 E 1 и C 1 D 1 обозначим D’ , D” .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Соединим точки B’ , C’ ; D’ , D” ; F’ , E’ .
Полученный семиугольник AB’C’D”D’E’F’ будет искомым сечением .
Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки F’ , B’ , D’ .
Упражнение 1 4
Решение. Проведем прямые F’B’ и F’D’ , и найдем их точки пересечения P и Q с плоскостью ABC .
Проведем прямую PQ . Обозначим R точку пересечения PQ и FC .
Точку пересечения F’R и CC 1 обозначим C’ .
Соединим точки B’ , C’ и C’ , D’ .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Через точку F’ проведем прямые, параллельные C’D’ и B’C’ , и их точки пересечения с AA 1 и EE 1 обозначим A’ и E’ .
Соединим точки A’ , B’ и E’ , D’ .
Полученный шестиугольник A’B’C’D’E’F’ будет искомым сечением .
Построить сечение пирамиды ABCD плоскостью, параллельной ребру AD и проходящей через точки E , F .
Упражнение 1 5
Решение. Соединим точки E и F .
Через точку F проведем прямую FG , параллельную AD.
Соединим точки G и E .
Полученный треугольник EFG будет искомым сечением.
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Построить сечение пирамиды ABCD плоскостью, параллельной ребру CD и проходящей через точки E , F .
Упражнение 1 6
Решение. Через точки E и F проведем прямые EG и FH , параллельные CD.
Соединим точки G и F , E и H .
Полученный четырехугольник EGFH будет искомым сечением.
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Построить сечение пирамиды ABCD плоскостью, проходящей через точки E , F , G .
Упражнение 17
Решение. Для построения сечения пирамиды, проходящего через точки E , F , G ,
проведем прямую EF и обозначим P её точку пересечения с BD .
Обозначим Q точку пересечения прямых PG и CD .
Соединим точки F и Q , E и G .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Полученный четырехугольник EFQG будет искомым сечением.
Построить сечение пирамиды SABCD плоскостью, проходящей через точки A , E , F .
Упражнение 18
Решение. Для построения сечения пирамиды, проходящего через точки E , F , G , проведем прямую EF и обозначим G её точку пересечения с DB .
Проведем прямые AG и CB . Обозначим P их точку пересечения.
Проведем прямую PF и обозначим Q её точку пересечения с SC .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Соединим точки A и F , A и E , E и Q .
Полученный четырехугольник AFQE будет искомым сечением.
Построить сечение пирамиды SABCD плоскостью, проходящей через точки E , F , G .
Упражнение 19
Решение. Для построения сечения пирамиды, проходящего через точки E , F , G ,
проведем прямую FG и обозначим P её точку пересечения с SB .
Проведем прямую PE и обозначим Q её точку пересечения с AB .
Проведем прямую GQ и обозначим R её точку пересечения с AD .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Проведем прямую RE и обозначим T её точку пересечения с SD .
Соединим точки T и F .
Полученный пятиугольник ETFGQ будет искомым сечением.
Построить сечение пирамиды SABCD плоскостью, параллельной AS и проходящей через точки E , F .
Упражнение 2 0
Решение. Соединим точки E и F .
Через точку F проведем прямую, параллельную AS , и обозначим G ее точку пересечения с AC .
Проведем прямую EG и обозначим H ее точку пересечения с AD .
Через точку H проведем прямую, параллельную AS , и обозначим I ее точку пересечения с SD .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Соединим точки I и F .
Полученный четырехугольник EFIH будет искомым сечением.
Построить сечение пирамиды SABCD плоскостью, параллельной BD и проходящей через точки E , F .
Упражнение 2 1
Решение. Проведем прямую EF и обозначим Q ее точку пересечения с AC .
Проведем прямую SO и обозначим P её точку пересечения с EF .
Через точку P проведем прямую GH , параллельную BD .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Соединим точки F , G , E , H .
Полученный четырехугольник FGEH будет искомым сечением.
Построить сечение пирамиды SABCDEF плоскостью, проходящей через точки A 1 , C 1 , E 1 .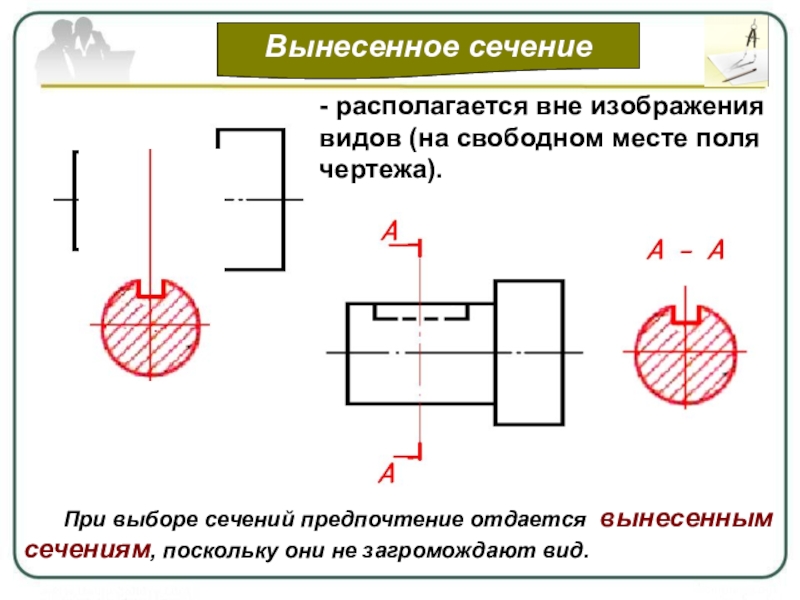
Упражнение 2 2
Решение. Найдем точку пересечения P прямой A 1 C 1 с плоскостью основания.
Найдем точку Q пересечения прямой E 1 C 1 с плоскостью основания.
Прямая PQ будет линией пересечения плоскости сечения и плоскости основания.
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Проведем прямую ED и обозначим R , её точку пересечения с прямой PQ .
Проведем прямую E 1 R и обозначим D 1 её точку пересечения с SD .
Аналогичным образом находятся точки F 1 и B 1 .
Шестиугольник A 1 B 1 C 1 D 1 E 1 F 1 будет искомым сечением.
Примеры построения сечений многогранников
Как известно, любой экзамен по математике содержит в качестве основной части решение задач. Умение решать задачи – основной показатель уровня математического развития.
Достаточно часто на школьных экзаменах, а так же на экзаменах, проводимых в ВУЗах и техникумах, встречаются случаи, когда ученики, показывающие хорошие результаты в области теории, знающие все необходимые определения и теоремы, запутываются при решении весьма простых задач.
За годы обучения в школе каждый ученик решает большое число задач, но при этом для всех учеников задачи предлагаются одни и те же. И если некоторые ученики усваивают общие правила и методы решения задач, то другие, встретившись с задачей незнакомого вида, даже не знают, как к ней подступиться.
Одной из причин такого положения является то, что если одни ученики вникают в ход решения задачи и стараются осознать и понять общие приёмы и методы их решения, то другие не задумываются над этим, стараются как можно быстрее решить предложенные задачи.
Многие учащиеся не анализируют решаемые задачи, не выделяют для себя общие приёмы и способы решения. В таких случаях задачи решаются только ради получения нужного ответа.
Так, например, многие учащиеся даже не знают, в чём суть решения задач на построение. А ведь задачи на построение являются обязательными задачами в курсе стереометрии. Эти задачи не только красивы и оригинальны в методах своего решения, но и имеют большую практическую ценность.
Благодаря задачам на построение развивается способность мысленно представлять себе ту или иную геометрическую фигуру, развивается пространственное мышление, логическое мышление, а так же геометрическая интуиция. Задачи на построение развивают навыки решения проблем практического характера.
Задачи на построения не являются простыми, так как единого правила или алгоритма для их решения не существует. Каждая новая задача уникальна и требует индивидуального подхода к решению.
Процесс решения любой задачи на построение – это последовательность некоторых промежуточных построений, приводящих к цели.
Построение сечений многогранников базируется на следующих аксиомах:
1) Если две точки прямой лежат в некоторой плоскости, то и вся прямая лежит в данной плоскости;
2) Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Теорема: если две параллельные плоскости пересечены третьей плоскостью, то прямые пересечения параллельны.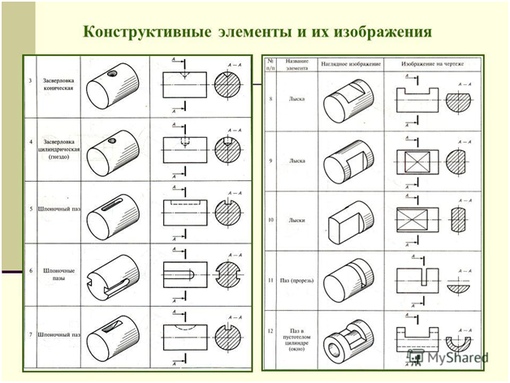
Примеры построения сечений многогранников
Построить сечение многогранника плоскостью, проходящей через точки А, В и С. Рассмотрим следующие примеры.
Метод следов
I. Построить сечение призмы плоскостью, проходящей через данную прямую g (след) на плоскости одного из оснований призмы и точку А.
Случай 1.
Точка А принадлежит другому основанию призмы (или грани, параллельной прямой g) – секущая плоскость пересекает это основание (грань) по отрезку ВС, параллельному следу g.
Случай 2.
Точка А принадлежит боковой грани призмы:
1) строится точка D, в которой плоскость грани пересекает данный след g;
2) проводится прямая через точки А и D.
Отрезок ВС прямой AD и есть пересечение данной грани с секущей плоскостью.
Концы отрезка ВС принадлежат и соседним граням. Поэтому описанным способом можно построить пересечение этих граней с секущей плоскостью.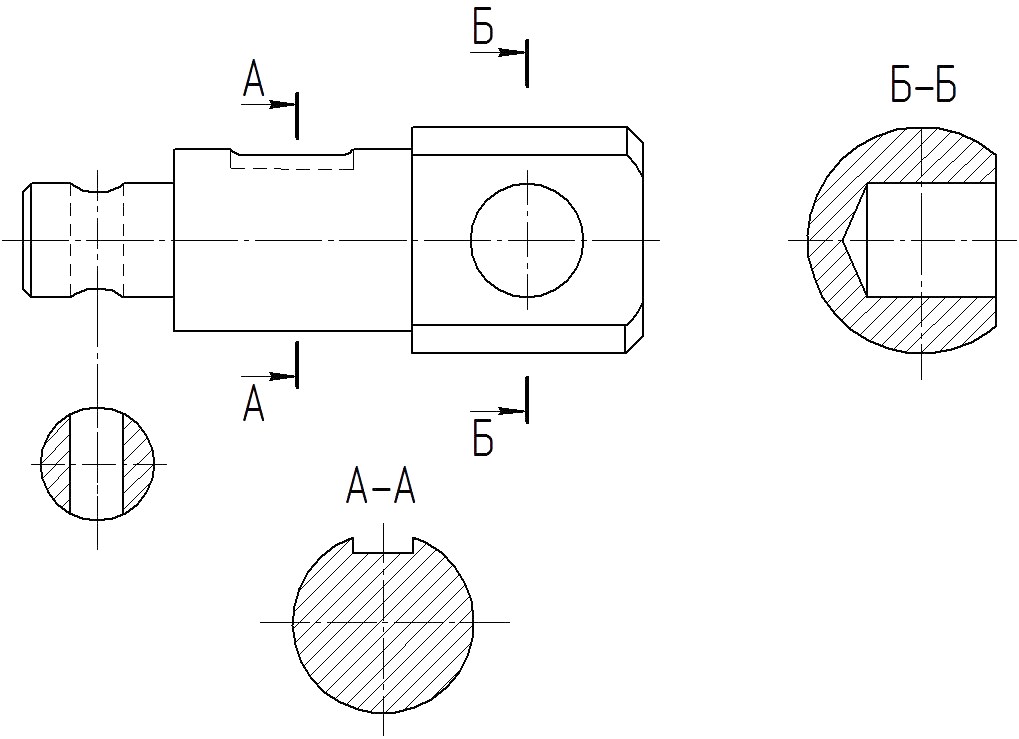
И т. д.
Случай 3.
Построение сечения четырехугольной призмы плоскостью, проходящей через прямую g в плоскости нижнего основания призмы и точку А на одном из боковых ребер.
II. Построить сечение пирамиды плоскостью, проходящей через данную прямую g (след) на плоскости основания пирамиды и точку А.
Для построения сечения пирамиды плоскостью достаточно построить пересечения ее боковых граней с секущей плоскостью.
Случай 1.
Если точка А принадлежит грани, параллельной прямой g, то секущая плоскость пересекает эту грань по отрезку ВС, параллельному следу g.
Случай 2.
Если точка А, принадлежащая сечению, расположена на грани, не параллельной грани следу g, то:
1) строится точка D, в которой плоскость грани пересекает данный след g;
2) проводится прямая через точки А и D.
Отрезок ВС прямой АD и есть пересечение данной грани с секущей плоскостью.
Концы отрезка ВС принадлежат и соседним граням. Поэтому описанным способом можно построить пересечение этих граней с секущей плоскостью. И т. д.
Случай 3.
Построение сечения четырехугольной пирамиды плоскостью, проходящей через сторону основания и точку А на одном из боковых ребер.
Задачи на построение сечений через точку на грани
1. Построить сечение тетраэдра АВСD плоскостью, проходящей через вершину С и точки М и N на гранях АСD и АВС соответственно.
Точки С и М лежат на грани АСD, значит, и прямая СМ лежит в плоскости этой грани (рис. 1).
Пусть Р – точка пересечения прямых СМ и АD. Аналогично, точки С и N лежат в грани АСВ, значит прямая СN лежит в плоскости этой грани. Пусть Q – точка пересечения прямых СN и АВ. Точки Р и Q принадлежат и плоскости сечения, и грани АВD. Поэтому отрезок РQ – сторона сечения. Итак, треугольник СРQ – искомое сечение.
2. Построить сечение тетраэдра АВСD плоскостью MPN, где точки M, N, P лежат соответственно на ребре АD, в грани ВСD и в грани АВС, причем MN не параллельно плоскости грани АВС (рис.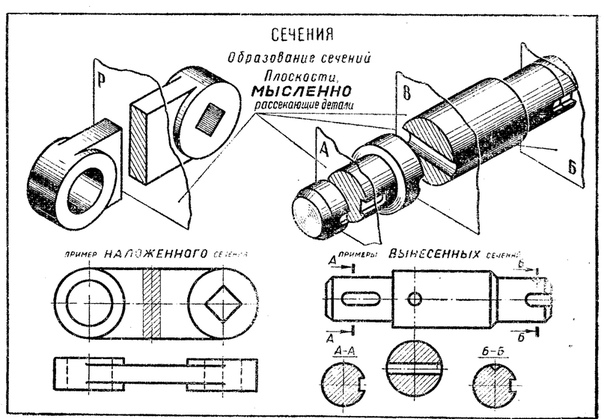
2).
Остались вопросы? Не знаете, как построить сечение многогранника?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Как рисовать сечения изогнутых и неправильных форм
Учитесь на знаниях сообщества. Эксперты добавляют свои идеи в эту совместную статью на основе ИИ, и вы тоже можете.
Это новый тип статьи, который мы начали с помощью ИИ, и эксперты продвигают его вперед, делясь своими мыслями непосредственно в каждом разделе.
Если вы хотите внести свой вклад, запросите приглашение, поставив лайк или ответив на эту статью.
Узнать больше
— Команда LinkedIn
Последнее обновление: 1 июля 2023 г.
Виды в разрезе — это распространенный метод инженерного черчения, позволяющий показать внутренние элементы объекта, которые не видны снаружи. Они особенно полезны для сложных или неправильных форм с кривыми, отверстиями или углублениями. В этой статье вы узнаете, как рисовать сечения изогнутых и неправильных форм, используя некоторые основные правила и примеры.
Правило 1: Разрежьте объект по секущей плоскости
Первый шаг к рисованию разреза — представить, что вы разрезаете объект по плоскости, проходящей через его внутреннюю часть. Секущая плоскость может быть параллельна, перпендикулярна или наклонена к основным видам объекта. Вы можете использовать пунктирную линию для обозначения секущей плоскости на виде спереди или сверху объекта. Направление секущей плоскости определяет ориентацию вида в разрезе.
Правило 2: Удалите материал над или за секущей плоскостью
Следующим шагом будет удаление материала, который находится над или за секущей плоскостью, и обнажите внутренние элементы объекта.
Вы можете использовать сплошную линию, чтобы очертить форму поперечного сечения объекта на виде в разрезе. Вы также можете использовать линии штриховки, чтобы заполнить область, представляющую поверхность разреза материала. Линии штриховки должны быть параллельными, равномерно расположенными и тонкими.
Правило 3: Идентифицируйте и маркируйте линии сечения
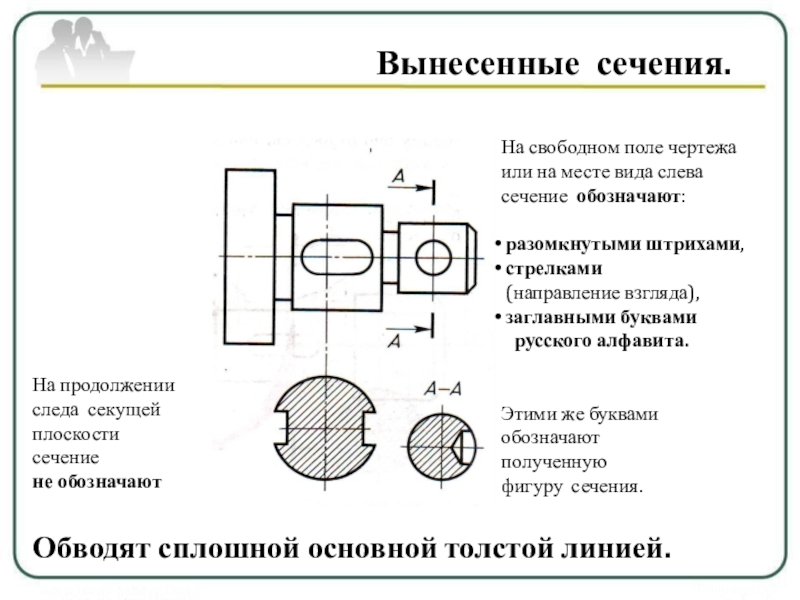
Линии сечения — это линии, которые показывают ребра или границы внутренних элементов, разрезаемых секущей плоскостью. Они могут быть прямыми, изогнутыми или неправильными в зависимости от формы объекта. Вы должны использовать тонкую линию, чтобы нарисовать линии сечения на виде в разрезе. Вы также должны пометить линии сечения буквами или цифрами, которые соответствуют секущей плоскости на главном виде. Например, если секущая плоскость помечена как A-A, линии сечения должны быть помечены как A-A на виде в разрезе.
Правило 4. Рисуйте скрытые линии только при необходимости
Скрытые линии — это линии, которые показывают ребра или границы внутренних элементов, которые не пересекаются секущей плоскостью, но скрыты от поля зрения.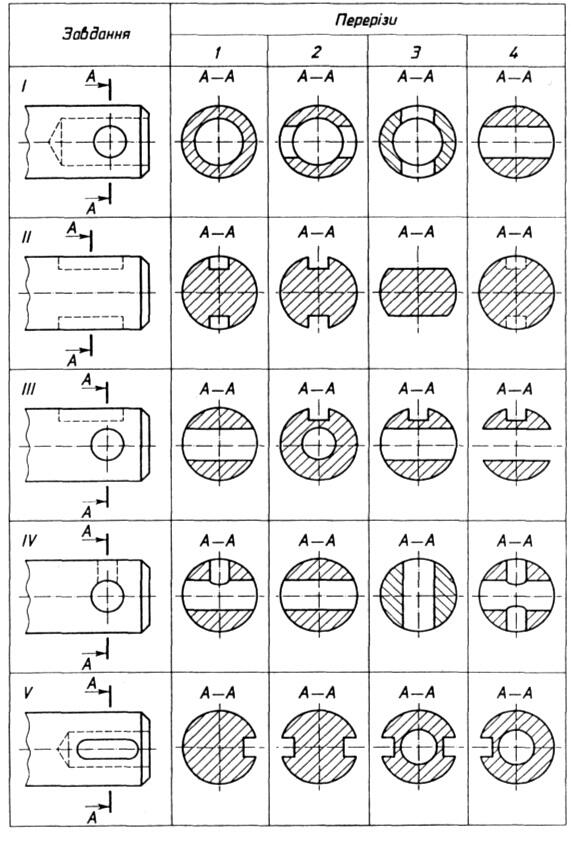
Они могут быть полезны, чтобы показать форму или расположение внутренних элементов, которые не видны на виде в разрезе. Однако следует избегать рисования скрытых линий, когда они не нужны или загромождают рисунок. Вы должны использовать пунктирную линию, чтобы нарисовать скрытые линии на разрезе.
Правило 5. Соблюдайте соглашения для криволинейных и неправильных форм
Существуют определенные правила, которых следует придерживаться при рисовании разрезов криволинейных и неправильных форм. Например, если объект имеет цилиндрическую или сферическую форму, вы должны нарисовать линии сечения в виде дуг, повторяющих кривизну объекта. Если объект имеет коническую или пирамидальную форму, вы должны нарисовать линии сечения в виде прямых линий, исходящих из вершины объекта. Если объект имеет сложную или неправильную форму, следует провести линии разреза как можно ближе к фактической форме объекта.
Правило 6: Проверьте точность и четкость вида в разрезе
Последним шагом является проверка точности и четкости вашего вида в разрезе.
Вы должны убедиться, что ваш вид в разрезе соответствует основному виду с точки зрения размеров, пропорций и ориентации. Вы также должны убедиться, что ваш вид в разрезе показывает все соответствующие внутренние особенности объекта без какой-либо двусмысленности или путаницы. Вы также должны убедиться, что ваш вид в разрезе соответствует стандартным символам, обозначениям и форматам инженерного чертежа.
Оцените эту статью
Мы создали эту статью с помощью ИИ. Что вы думаете об этом?
Это здорово Это не так здорово
Спасибо за ваш отзыв
Ваш отзыв является частным. Поставьте лайк или отреагируйте, чтобы перенести разговор в свою сеть.
Команда построения поперечных сечений — База знаний CivilGEO
Поперечные сечения располагаются с интервалами вдоль ручья для того, чтобы охарактеризовать пропускную способность ручья и прилегающей поймы.
Они должны проходить через всю пойму и должны быть перпендикулярны ожидаемым линиям потока. Иногда необходимо расположить поперечные сечения в криволинейном или криволинейном направлении, чтобы выполнить это требование. Они не должны пересекаться друг с другом и должны оставаться перпендикулярными основному каналу.
Как добавить поперечное сечение в HEC-RAS?
Команда Draw Cross Sections позволяет пользователю рисовать поперечное сечение в представлении карты, а также извлекать геометрию поперечного сечения из подстилающей поверхности земли.
Чтобы использовать команду Draw Cross Sections , выполните следующие шаги:
- В ленточном меню Input выберите пункт меню Cross Sections , а затем выберите команду Draw Cross Sections .
- Отобразится диалоговое окно Начертить поперечные сечения .
В следующих разделах описывается команда «Начертить поперечные сечения» и как взаимодействовать с диалоговым окном выше.
Обратите внимание, , что в программном обеспечении предусмотрена комбинация клавиш ( Ctrl+D ), которая автоматически запускает команду Начертить поперечные сечения . Нажатие клавиши Ctrl+D позволяет пользователю рисовать поперечные сечения непосредственно в представлении карты, не взаимодействуя с меню ленты или 9диалоговое окно 0109 Draw Cross Sections . Чтобы узнать, как рисовать поперечные сечения с помощью сочетания клавиш ( Ctrl +D ), обратитесь к этой статье в нашей базе знаний.
Рисование полилинии поперечного сечения
Этот раздел используется для интерактивного рисования полилинии в представлении карты, чтобы назначить ее в качестве поперечного сечения. Настоятельно рекомендуется, чтобы остальные входные параметры диалогового окна были определены до рисования поперечных сечений в представлении карты. Эти параметры определяют информацию, например, как должны быть пронумерованы идентификаторы поперечных сечений, откуда будет извлекаться геометрия поперечных сечений и следует ли назначать пикеты береговых сечений.
Когда вы будете готовы построить поперечные сечения в представлении карты, нажмите кнопку [Нарисовать] . Диалоговое окно Draw Cross Sections временно исчезнет, а в строке состояния появится подсказка, информирующая пользователя о дальнейших действиях. В представлении карты нарисуйте ломаную линию через реку от одной стороны к другой, чтобы определить поперечное сечение. Обратите внимание, что нарисованная полилиния должна пересекать существующий участок реки, иначе программа сообщит об этом как о проблеме. Однако пользователь может рисовать в любом направлении через реку (т. е. слева направо или справа налево), поскольку программное обеспечение определит направление поперечного сечения на основе ранее определенного направления течения реки.
После того, как полилиния поперечного сечения была начерчена, либо щелкните правой кнопкой мыши и выберите Готово из отображаемого контекстного меню, либо нажмите клавишу [Enter] .
Затем программа построит поперечное сечение и предложит пользователю нарисовать следующее поперечное сечение. Закончив рисовать поперечные сечения, щелкните правой кнопкой мыши и выберите Cancel из отображаемого контекстного меню или нажмите клавишу [Esc] . Программное обеспечение вернет пользователя в диалоговое окно.
Этот разрез используется для определения речной пикетации построенных створов. После построения полилинии поперечного сечения программа автоматически рассчитает речной пикет для поперечного сечения на основе других поперечных сечений, уже присвоенных участку реки, и параметров, определенных в этом сечении.
Для строящихся разрезов значение пикетажа после запятой можно определить с помощью Decimal Precision Spin control. Поперечные сечения могут быть пронумерованы с фиксированным шагом или по цепочке рек на участке реки. Цепь реки может быть в милях или футах при работе в единицах США или в километрах или метрах при работе в метрических единицах (СИ).
Эта панель с вкладками используется для определения спецификаций извлечения геометрии для нарисованных поперечных сечений.
Этот необязательный раздел используется для определения источника данных высот, который будет использоваться для извлечения геометрии поперечного сечения. В зависимости от выбранного типа источника данных о высотных отметках предоставляются различные параметры для указания дополнительных данных о высотных отметках.
Обратитесь к этой статье в нашей базе знаний для получения информации о типах данных о высоте местности, которые можно использовать для построения поперечных сечений.
Если флажок «Извлечь данные высоты» не установлен, последующие разделы под ним будут недоступны (т. е. выделены серым цветом). Кроме того, при создании поперечного сечения геометрия не создается. Поперечное сечение будет представлять собой плоскую горизонтальную линию с отметкой 0.
Это дополнительное сечение используется для управления объемом геометрии поперечного сечения, извлекаемой для нарисованной полилинии.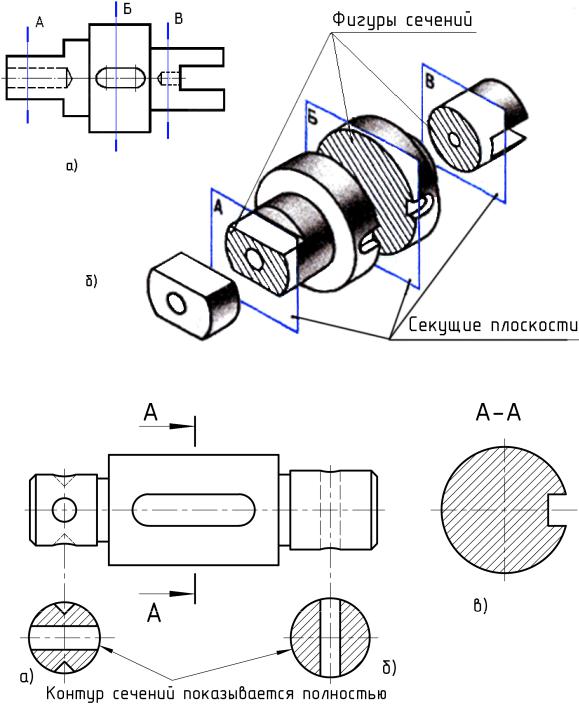
Это гарантирует создание достаточно глубокого поперечного сечения по обеим сторонам участка реки. Программное обеспечение попытается извлечь данные о геометрии поперечного сечения на глубину, указанную в пределах указанной максимальной ширины поперечного сечения.
Если нарисованная полилиния не выходит наружу достаточно далеко, чтобы получить указанную глубину поперечного сечения, программа автоматически продлит линию поперечного сечения дальше наружу. Аналогичным образом, если нарисованная полилиния выходит за пределы заданной глубины слишком далеко, программа автоматически обрежет нарисованную линию поперечного сечения.
Прочие данные
Эта панель с вкладками используется для определения местоположений банка каналов на основе параметров, выбранных для начерченных поперечных сечений.
Назначить станции банка
Этот необязательный раздел используется для создания местоположений банка каналов HEC-RAS на основе выбранной опции. Доступны следующие опции:
Определить по ширине канала
Эта опция назначит станции банка, используя определенную ширину канала.
Программа сначала определит, где на поперечном сечении находится тальвег. Затем он будет равномерно двигаться наружу от тальвега, пока не будет достигнута требуемая ширина канала.
Определить по глубине канала
Эта опция назначит станции банка, используя предполагаемую нормальную глубину потока и максимальное расстояние поиска по ширине канала. Программа сначала определит, где на поперечном сечении находится тальвег. Затем он будет двигаться наружу от тальвега до тех пор, пока не будет достигнута запрошенная глубина канала в пределах указанной максимальной ширины канала.
Определить по банкам полилиний/многоугольников
Эта опция назначит станции банка с помощью выбранных полилиний или полигонов. Программа сначала определит, где на поперечном сечении находится тальвег. Затем он будет двигаться наружу от тальвега до тех пор, пока не будет достигнута предварительно выбранная полилиния берега или край многоугольника.
При построении поперечного сечения программа автоматически назначит шероховатость Мэннинга по умолчанию для левого берега, русла и правого берега на панели Шероховатость .
Однако пользователь может изменить значения по умолчанию на любые желаемые.
Кроме того, программа автоматически определяет длину потока до следующего поперечного сечения ниже по течению. Если новое поперечное сечение вставляется между двумя соседними поперечными сечениями, программное обеспечение автоматически регулирует длину потока следующего вышестоящего поперечного сечения с учетом вставки нового поперечного сечения.
Программное обеспечение также позволяет пользователю определить более трех значений n Мэннинга для любого выбранного поперечного сечения. Пользователь может указать горизонтально изменяющиеся значения n Мэннинга, чтобы определить несколько областей с меньшей шероховатостью для выбранного поперечного сечения.
После построения поперечного сечения пользователь может дважды щелкнуть поперечное сечение в представлении карты, чтобы отобразить диалоговое окно Данные поперечного сечения .
В Крестовина Секция Геометрия приведенного выше диалогового окна, пользователь может установить флажок Горизонтальная шероховатость , чтобы активировать столбец Горизонтальная шероховатость , и ввести различные значения n Мэннинга.