Формула расчета уклона: Расчёт уклона по расстоянию и превышению. Онлайн калькулятор.

8 800 301-15-21

+7 (351) 214-97-71

Как рассчитать угол наклона крыши

Как рассчитать угол наклона крыши от компании мир Світ Покрівлі

Крыша частного дома, строящаяся по индивидуальному плану, может встречаться в разном формате. При этом наклонный размер скатов соразмерен конструкционным особенностям, присутствию чердачного помещения, а также погодным условиям окружающей среды. Этот параметр представляет собой размер между горизонтальным сегментом конструкции и верхней частью крыши. В расчетной документации он показан в градусах или процентном соотношении.

Измерять уклон можно с помощью специальных приспособлений или математическим способом. В первом случае задействуется специальный рельсовый уклономер, хотя в последнее время появились и более современные инструменты – геодезические приборы, равные в капсулах или электронному типу.

МАТЕМАТИЧЕСКИЙ РАСЧЕТ

Простейшим методом обозначения наклона углов является тот, что не предполагает использование специальных геодезических приборов. Чтобы обозначить этот параметр, достаточно знать два показателя:

Н – высоту по вертикали – часто от карнизной части к коньку; L – величину по горизонтали – с низа ската до верхней части.

Формула основных расчетов в данной ситуации выглядит следующим образом:

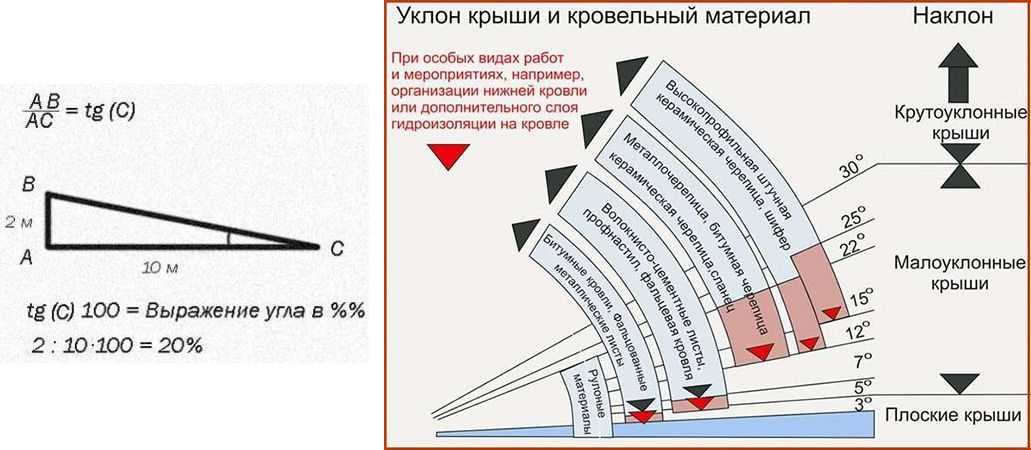
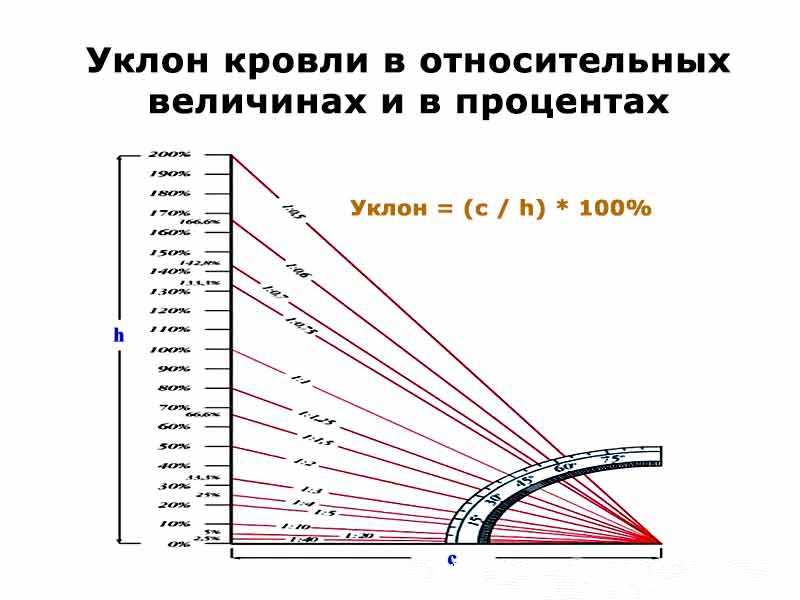
i = Н: L

Полученная в результате цифра умножающаяся на 100-тогда будет известна наклонный угол в процентном показателе. Если же данные нужны в градусах, тогда необходимо воспользоваться особой таблицей, в которой приведено соотношение:

ЗАВИСИМОСТЬ Угла СКАТА ОТ КРОВЕЛЬНОГО МАТЕРИАЛА

Каждый тип конструкции крыши имеет свои достоинства и недостатки. Некоторые из них требуют усиленной гидроизоляции, некоторые менее сложны в монтаже. Все это лучше учесть при подборе материалов, которые будут использованы в работе. Как правило, производители дают подробную информацию по поводу рекомендуемого уклона кровли. К примеру, на пологих крышах обычно задействуют рулонные материалы, а при крутизне в 15 градусов искусственные изделия будут недопустимы. Более подробные сведения по этому вопросу можно найти в нижеследующей таблице.

КАК ВЗАИМОЗАВИСИМЫЙ УГЛОК КРЫШИ И ГАБАРИТЫ МАНСАРДНОГО ПОМЕЩЕНИЯ

Расчет высоты крыши подразумевает прямую связь с размером полезной площади пространства под скатами. Чем она выше, тем просторнее будет полезна площадь внутри дома.

ИЗМЕНЕНИЕ ПОЛЕЗНОЙ ПЛОЩАДИ В ЗАВИСИМОСТИ ОТ ВЫСОТИ КРОВЛИ

Поскольку показатель полезной высоты мансардного помещения обычно находится на уровне 2,5 – 3 м, то и поднятие кровли с учетом используемого материала выше 5 метров считается невыгодным. Если учитывать эти данные, то величина в 25 градусов для построек с одно- или двускатной крышей можно считать самой оптимальной. При необходимости возведения кровли мансардного типа ее часть вверху может допускать уклон в 10 – 20 градусов, а внизу – 50 – 80. При этом размещение самого пространства под крышей предполагает большую вариативность, которая зависит от того, какая система кровли будет применена.

Из всего вышесказанного можно заключить, что для большей части нашей страны наиболее подходящим будет считаться уклон кровли в пределах 25 – 35 градусов. Такая конструкция не даст снегу и дождю задерживаться на поверхности и прекрасно выдержит сильные ветры. А верно разработанный проект будет гарантировать большой размер площади мансардного помещения.

Заказывайте только у нас – самые качественные кровельные материалы: Металлочерепица, Фальцевая кровля, Металлопрофиль (профнастил), Битумная черепица, Композитная черепица.

Аксессуары для кровли и та фасаду: Гидроизоляция, пароизоляция, Водосточная система, Мансардные окна, Минеральная вата, Пиломатериалы, Софит.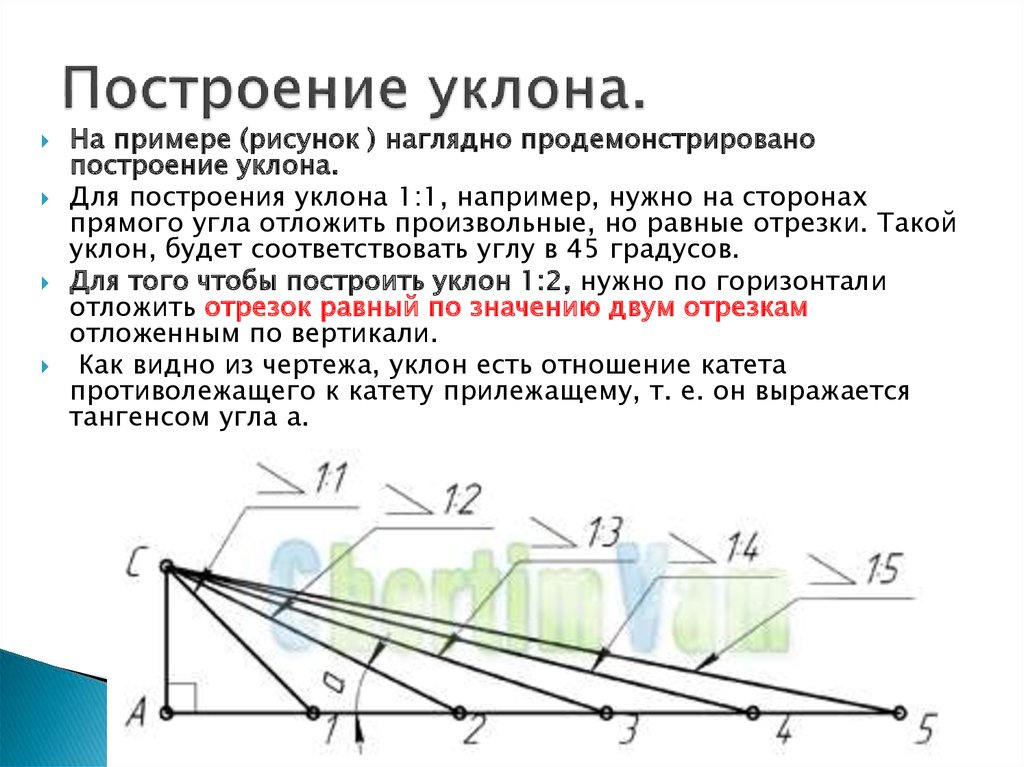

Все виды монтажных работ от лучших специалистов: Монтаж металлочерепицы, Монтаж металлопрофиля, Монтаж фальцевой кровли, Монтаж битумной черепицы, Монтаж композитной черепицы.

— что такое формула уклона? Уравнение, примеры

Формула уклона используется для расчета наклона или крутизны линии. Он находит применение при определении наклона любой линии путем нахождения отношения изменения по оси у к изменению по оси х. Наклон линии определяется как изменение координаты «у» по отношению к изменению координаты «х» этой линии.

Что такое формула уклона?

Формула наклона относится к формуле, используемой для расчета крутизны линии и определения ее наклона. Для вычисления наклона линий можно использовать координаты x и y точек, лежащих на линии. Другими словами, это отношение изменения по оси у к изменению по оси х.

Формула уклона

Формула для расчета уклона имеет вид 003

где m — наклон линии, x ₁ , x ₂ — координаты по оси x, а y ₁ , y ₂ — координаты по оси y.

Вывод формулы наклона

Координаты x и y линии используются для расчета наклона линии. Чистое изменение координаты y равно Δy, а чистое изменение координаты x равно Δx. Таким образом, изменение координаты y по отношению к изменению координаты x можно записать как

м = Δy/Δx

где

• м — уклон
• Δy — изменение координаты y
• Δx — изменение координаты x

Мы знаем, что тангенс θ также является наклоном линии, где θ — это угол, образуемый линией с положительным направлением оси x.

И, tanθ = высота/основание

Так как высота/основание между любыми двумя заданными точками = (y ₂ – y ₁ )/(x ₂ – x ₁ )

Таким образом, уравнение наклона имеет вид m = tanθ = Δy/Δx

Из графика видно: у ₁ )

Таким образом, формула наклона задается как: Уклон = m = (y ₂ – y ₁ )/(x ₂ – x ₁ )

Уравнение наклона

сечения, формула наклона может быть использована для определения наклона любой линии. Таким образом, уравнение, которое можно использовать для определения этого наклона, можно записать в виде 9.0099 m = подъем/спуск = tanθ = Δy/Δx = (y ₂ – y ₁ )/(x ₂ – x ₁ )

где

• м4 – уклон
• Δy — изменение координаты y
• Δx — изменение координаты x
• θ — угол, образуемый линией с положительной осью x

Кроме того, уравнение наклона любой линии с использованием уравнения линии может быть задано как
у = mx + b

где,

• м – уклон линии
• b – точка пересечения по оси y линии
.

Рассмотрим применение формулы наклона в следующих решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры использования формулы наклона

Пример 1: Найдите наклон линии с координатами (2,9) и (4,1)?

Решение:

Найти: Наклон прямой с координатами (2,9) и (4,1)

Дано, (x ₁ , y ₁ ) = (2, 9) и (x ₂ , y ₂ ) = (4, 1)

Формула наклона:

м = (1 − 9)/(4 − 2)

м = -8/2 = -4

Ответ: Наклон данной прямой = -4

Пример 2: Определите значение b, если наклон прямой, проходящей через точки (b, 7) и (8, -5), равен 6

Решение:

Найти: значение b

Дано, Наклон = m = 6, Точки: (x ₁ , y ₁ ) = (b, 7) и (x ₂ , у ₂ ) = (8, -5)
Мы знаем, что Уклон (м) = (y ₂ – y ₁ )/(x ₂ – x ₁ )
6 = (-5-7)/(8-б)
6 = (-12)/(8-б)
-2= (8-б)
-2-8 = -б,
b = 10
Ответ: Значение b = 10.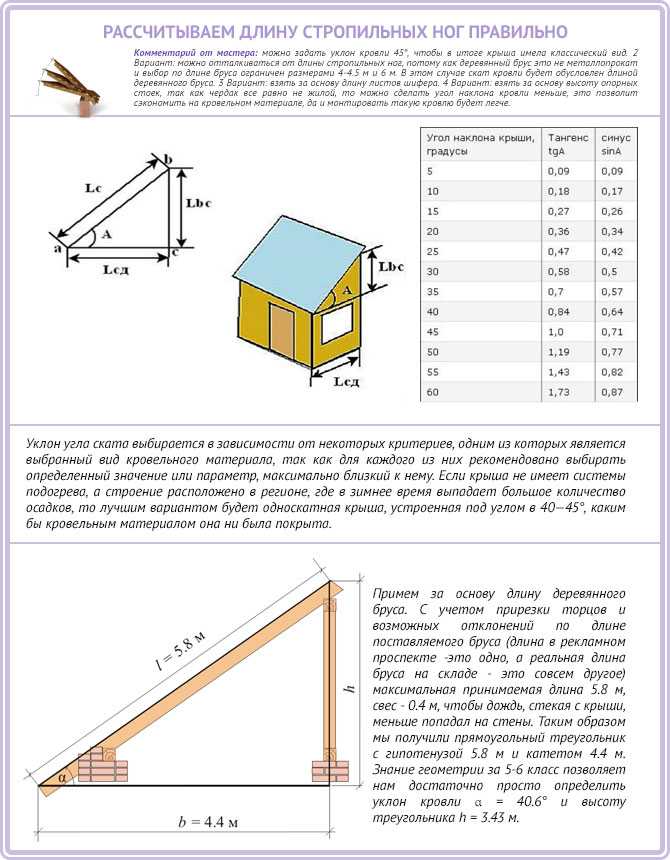

Пример 3: Если угол, образуемый линией с положительной осью y, равен 30°, то каково значение наклона линии ?

Решение:

Найти: наклон прямой

Дано: Угол, образуемый линией с положительной осью ординат = 30°

Мы знаем, что если линия образует угол 30° с положительной оси y, то он составляет угол 120° от положительной оси x. Следовательно, значение наклона линии равно tg120° = -√3

Ответ: Значение наклона линии = -√3

Часто задаваемые вопросы о формуле наклона

Что такое формула наклона в геометрии?

В геометрии формула наклона определяется как формула для вычисления наклона любой линии путем нахождения отношения изменения по оси Y к изменению по оси X.

Что означает m в формуле уклона?

В формуле уклона m обозначает уклон, который рассчитывается как m = (y ₂ – y ₁ )/(x ₂ – x ₁ ) = Δy/Δx

Для чего используется формула наклона?

Формула наклона используется для расчета крутизны линии, а координаты линий x и y используются для того же. Мы знаем, что наклон линии является одной из наиболее важных характеристик линии, поскольку он помогает измерить скорость изменения.

Как рассчитать уклон, используя формулу уклона?

Наклон линии можно рассчитать по следующим формулам:

Когда заданы координаты:

• Шаг 1: Найдите координаты линии.
• Шаг 2: Подставьте их значения в формулу (m) = (y ₂ – y ₁ )/(x ₂ – x ₁ )

Если задан угол:

• Шаг 1: Определите угол, образуемый с осью.
• Шаг 2: Подставьте значение в формулу, m = tanθ

Что такое уравнение наклона линии?

Уравнение наклона любой линии можно рассчитать по следующей формуле:

м = подъем/пробег = tanθ = Δy/Δx = (y ₂ – y ₁ )/(x ₂ – x ₁ )

где,

• м – уклон
• Δy — изменение координаты y
• Δx — изменение координаты x
• θ — угол, образуемый линией с положительной осью x

Уравнение наклона с использованием уравнения прямой задается как y = mx + b, здесь m — это наклон, а b — точка пересечения с осью y.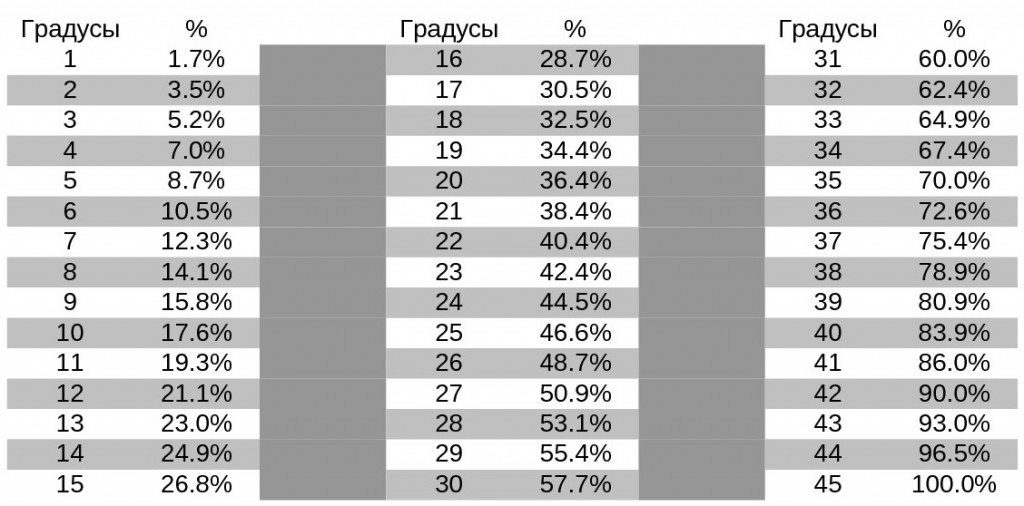

Найти наклон линии с помощью уравнения наклона

• Курсы
• Поиск

• Зарегистрироваться
• Войти

Домашняя страница

1. 6 40Alge
2. 6 40Alge 330 >Линейные функции

Справка

Нажми на математику 🤔 и получай лучшие оценки! 💯Присоединяйтесь бесплатно

Получите максимум от просмотра этой темы в своем текущем классе. Выберите свой курс сейчас .

Интро

Начать просмотр

Уроки

1. Обзор: Наклоны линий

   Обзор: Наклоны линий

Уроки

1. Определите уклон с помощью функции метод
   
   
   1. Линия A
   2. Линия B
2. Определите наклон на основе графика: положительный, отрицательный, нулевой или неопределенный, и проверьте
   
   
   1. Линия A
   2. Линия B
   3. Линия C
   4. Линия D
3. Даны две точки прямой, определяя наклон с помощью m=(y2−y1)/(x2−x1)m = (y_2 – y_1) / (x_2 – x_1) m=(y2​−y1​)/(x2​−x1​)
   1. (−2,7)(-2,7)(−2,7) и (6, −6)(6, -6)(6,−6)
   2. (53,67)(\frac{5}{3}, \frac{6}{7})(35​,76​) и ( 35,−83)(\frac{3}{5} , \frac{-8}{3})(53​,3−8​)
4. Расположите склоны от самого плоского до самого крутого.
   1. −3,12,34,32-3,\frac{1}{2},\frac{3}{4},\frac{3}{2} −3,21​,43​,23​
5. Два равнобедренных треугольника имеют одинаковую высоту. Наклоны сторон треугольника A в два раза больше наклонов соответствующих сторон треугольника B. Как соотносятся длины их оснований?

   Присоединиться бесплатно!

   StudyPug — это платформа помощи в обучении, охватывающая математику и естественные науки с 4 класса до второго курса университета. Наши видеоуроки, неограниченное количество практических задач и пошаговые объяснения обеспечат вам или вашему ребенку всю необходимую помощь для освоения концепций. Кроме того, это весело — с достижениями, настраиваемыми аватарами и наградами, которые поддерживают вашу мотивацию.

   • Учащиеся
   • Родители

   • Регистрация бесплатно

   • Легко видеть ваш прогресс

     Мы отслеживаем ваш прогресс по теме, чтобы вы знали, что вы сделали. В режиме просмотра курса вы можете легко увидеть, какие темы есть, и прогресс, которого вы достигли по ним. Заполните кольца, чтобы полностью освоить этот раздел, или наведите указатель мыши на значок, чтобы увидеть больше деталей.

   • Воспользуйтесь нашими учебными пособиями

     Последнее просмотренное

     Практика точности

     Предлагаемые задания

     Получите быстрый доступ к теме, которую вы сейчас изучаете.

     Посмотрите, насколько хорошо проходят ваши тренировки.

     Будьте в курсе наших ежедневных рекомендаций.

     Присоединяйтесь бесплатно

   • Получайте достижения по мере обучения

     Максимально используйте свое время, используя StudyPug для достижения своих целей. Зарабатывайте забавные маленькие значки, чем больше вы смотрите, практикуетесь и используете наш сервис.

   • Создайте и настройте свой аватар

     Поиграйте с нашим забавным конструктором аватаров, чтобы создать и настроить собственный аватар на StudyPug.