404 Cтраница не найдена
Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО “МГТУ” и согласны с нашими правилами обработки персональных данных.
Размер:
AAAИзображения Вкл. Выкл.
Обычная версия сайтаК сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Педагогический (научно-педагогический) составОбозначение шероховатости поверхности на чертеже по ГОСТу
Содержание
- Правила обозначения шероховатости поверхности
- Какие символы применяют для обозначения шероховатости
Одним из условных обозначений на чертеже, необходимых для создания и производства качественной детали, является шероховатость поверхности.
Ее показатель напрямую влияет на то, каким получится чертеж и конечная деталь.
В этой статье я расскажу, как обозначается шероховатость и какие правила нанесения существуют.
Все нюансы обозначения регулирует ГОСТ 2789-73.
Показатель шероховатости выбирают исходя из роли детали в механизме, в котором планируется ее использование.
Но шероховатость — не то, с чего нужно начинать работу над чертежом. Для начала нужно поработать с линиями: первый этап предполагает нанесение тонких линий. После этого обозначается шероховатость, а затем — контур выделяется четкими плотными линиями.
Чтение шероховатости на чертеже предполагает, что вы знаете определенные правила ее нанесения и как именно выглядят условные обозначения шероховатости.
Правила обозначения шероховатости поверхности:
- шероховатость обозначается в виде галочки. Важно запомнить, что ее не указывают перевернутой относительно линии плоскости детали, и учитывать наличие осей центра вращения.
В последнем случае чтобы обозначить размеры шероховатости и классы, могут быть использованы противоположные поверхности; - информация касательно шероховатости может указываться на выносной полке;
- шероховатость указывается на стороне детали, удобной для поднесения инструмента для резки. Это указывает на специфику работы по образованию поверхности;
- если для всей поверхности детали характерна одинаковая шероховатость, то это указывается не на самой детали, а в правом верхнем углу чертежа. На чертеже указывают и параметры шероховатости для всех поверхностей. Если поверхность особая, то шероховатость указывают прямо на ней;
- резьбовая поверхность тоже может служить местом для нанесения шероховатости. Вместе с другими параметрами ее указывают на выноске, когда не хватает места.
В последнем случае чтобы обозначить размеры шероховатости и классы, могут быть использованы противоположные поверхности;Самый часто используемый знак шероховатости — перевернутая галочка. Означает, что тип обработки не устанавливается.
Если в галочке есть перемычка, то это значит, что необходима обработка с удалением материала.
А вот этот вариант не предполагает удаление материала.
Указывает на класс. Это среднеарифметический показатель отклонения профиля. Имеет числовое выражение. По нему определяют класс шероховатости, а после — во время обработки контролируют качество поверхности.
Обозначает неровности профиля по 10-ти точкам.
Привычная нам галочка говорит о том, что перед нами часть поверхности.
Если есть пояснительные надписи, то они обозначаются вот таким символом.
Пример условного обозначения шероховатости на чертеже символом с полкой относительно основной надписи.
Не нашли ответов на вопросы? У вас есть возможность обратиться за помощью к опытным экспертам Studently.
символов GD&T | Условия GD&T | Глоссарий геометрических размеров и допусков
Справочный центр GD&T
Виртуальная база знаний GD&T
Бесплатная 15-дневная пробная версия!
GD&T и инженерные ресурсы
Советы по GD&T, символы, викторина по GD&T и каталог продукции
Свяжитесь с нами
Советы и символы GD&T
Краткий справочник, когда вам это нужно
Свяжитесь с нами
Онлайн-викторина GD&T
Проверьте свои знания GD&T
Свяжитесь с нами
Символы GD&T с определениями
Ниже приведены символы GD&T вместе с их определениями, которые включены в стандарт ASME Y14.
5.
Символ со всех сторон
Указывает, что допуск применяется ко всем поверхностям вокруг детали.
Спецификация по всему периметру
В дополнение к общему профилю допуска поверхности существует возможность указать, что допуск применяется ко всему полю чертежа. Важно понимать, что эта спецификация, будь то в общем примечании или на поле чертежа, применяется, ЕСЛИ НЕ УКАЗАНО ИНОЕ.
Вокруг этой стороны линии разъема
Чтобы применить требование ко всем элементам вокруг одной стороны линии разъема, на линии выноски отображается графический символ для всех элементов вокруг этой стороны линии разъема.
По всей этой стороне линии разъема
Чтобы применить требование ко всем элементам по всей одной стороне линии разъема, графический символ для всей этой стороны линии разъема отображается на линии выноски.
Угловатость
Состояние поверхности, оси или центральной плоскости, расположенной под заданным углом от базовой плоскости или оси.
Длина дуги
Указывает, что размер представляет собой длину дуги, измеренную на криволинейном контуре. Символ размещается над размером.
Основной размер
Используется для описания точного размера, профиля, ориентации или местоположения элемента. Базовый размер всегда связан с рамкой управления элементом или целевой базой. (теоретически точный размер в ISO)
Между
Чтобы указать, что допуск профиля применяется к нескольким смежным элементам, буквы могут обозначать, где начинается и заканчивается допуск профиля. Эти буквы обозначаются символом между (с 1994 г.) или словом между на рисунках, сделанных в более ранних версиях Стандарта.
Окружность
Описывает состояние на поверхности вращения (цилиндр, конус, сфера), когда все точки поверхности пересекаются какой-либо плоскостью.
ПодробнееКонцентричность
Описывает состояние, при котором два или более элемента в любой комбинации имеют общую ось.
Больше не доступно в стандарте 2018 года.
Конический конус
Используется для обозначения конуса для конических конусов. Этот символ всегда отображается вертикальной ногой слева.
Непрерывный элемент
Примечание НЕПРЕРЫВНЫЙ ПРИЗНАК или символ непрерывного элемента используется для обозначения группы из двух или более элементов размера, когда существует требование, чтобы они геометрически рассматривались как один элемент размера. Хотя в определении упоминаются только элементы размера, есть пример применения CF к паре плоских элементов.
Контролируемый радиус
Создает зону допуска, определяемую двумя дугами (минимальный и максимальный радиусы), которые касаются соседних поверхностей. Там, где задан контролируемый радиус, контур детали в пределах серповидной зоны допуска должен представлять собой плавную кривую без плоских поверхностей или разворотов. Кроме того, радиусы, взятые во всех точках контура детали, не должны быть ни меньше указанного минимального предела, ни больше максимального предела.
Зенковка/Цековка
Используется для обозначения цековки или цековки. Символ предшествует размеру цековки или цековки без пробела.
Зенковка
Используется для обозначения зенковки. Символ предшествует размерам зенковки без пробела.
Цилиндричность
Описывает состояние поверхности вращения, при котором все точки поверхности равноудалены от общей оси.
ПодробнееЭлемент базы
Фактический элемент компонента, используемый для установки базы.
Базовая цель
Заданная точка, линия или область на детали, которая используется для установки базовой базовой плоскости для операций производства и контроля.
Альтернативный опорный объект
Заданная точка, линия или область на детали, которая используется для установки опорной плоскости при изготовлении и контроле.
Символ перемещения ИГД
Этот символ указывает на то, что имитатор ИГД не закреплен в своем базовом положении и может свободно перемещаться.
Глубина / Глубина
Используется для обозначения того, что размер относится к глубине объекта. Этот символ предшествует значению глубины без пробела между ними.
Диаметр
Указывает круговой элемент при использовании в поле чертежа или указывает, что допуск является диаметральным при использовании в рамке управления элементом.
Начало размера
Означает, что размер исходит из плоскости, установленной более короткой поверхностью, а пределы размеров применяются к другой поверхности.
Динамический модификатор зоны допуска профиля
Новое в версии 2018 и используется с допуском профиля. Функция динамического профиля состоит в том, чтобы позволить контролировать форму независимо от размера.
Рамка контроля характеристик
Представляет собой прямоугольную рамку, содержащую символ геометрических характеристик, а также допуск формы, биения или расположения. При необходимости ссылки на датумы и модификаторы, применимые к элементу или базам, также содержатся в поле.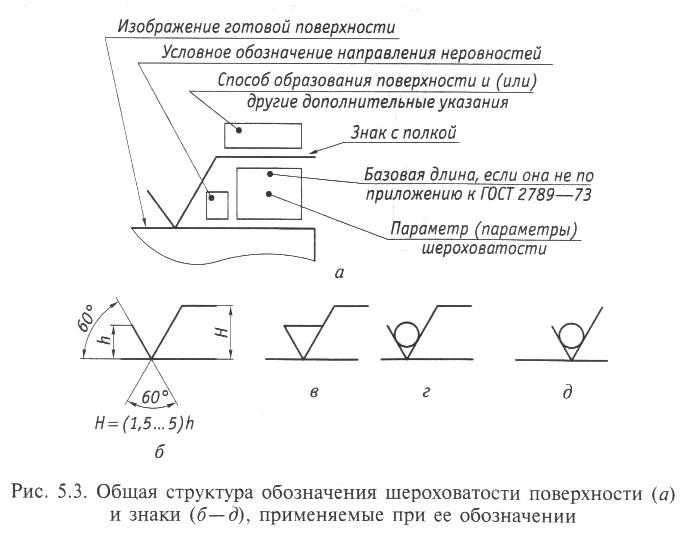
Плоскостность
Состояние поверхности, все элементы которой лежат в одной плоскости.
ПодробнееИзменения в свободном состоянии
Термин, используемый для описания деформации детали после устранения сил, приложенных во время производства.
From-To
Новое в 2018 году для направления, в котором применяется допуск или другое требование.
Символ Независимости
Символ Независимости применяется к измерению размера, чтобы применить принцип независимости к обычным элементам размера и отменить Правило №1.
Наименьшее состояние материала (LMC)
Подразумевает такое состояние элемента размера, при котором он содержит наименьшее (минимальное) количество материала, например, наибольший размер отверстия и наименьший размер вала. Это противоположно максимальному материальному состоянию.
Максимальное состояние материала (MMC)
Состояние детали, при котором она содержит максимальное количество материала в установленных пределах размера.
То есть: минимальный размер отверстия и максимальный размер вала.
Подвижные опорные цели
Символ подвижной опорной цели может использоваться для обозначения перемещения имитатора опорных элементов опорной цели.
Количество мест
X используется вместе со значением, чтобы указать, сколько раз размер или элемент повторяется на чертеже.
Параллелизм
Состояние поверхности, линии или оси, которые во всех точках равноудалены от базовой плоскости или оси.
ПодробнееЛинии разъема
На чертежах отливок, поковок и формованных деталей изображаются в виде воображаемой линии, выходящей за пределы детали на соответствующих видах, с добавленным символом линии разъема.
Перпендикулярность
Состояние поверхности, оси или линии, которая составляет 90 градусов. От базовой плоскости или базовой оси.
ПодробнееПоложение
Определяет зону, в пределах которой ось или центральная плоскость элемента могут отличаться от истинного (теоретически точного) положения.
Профиль линии
Это условие, допускающее равномерное изменение профиля, одностороннее или двустороннее, вдоль линейного элемента объекта.
ПодробнееПрофиль поверхности
Это условие, допускающее равномерное изменение профиля, одностороннего или двустороннего, на поверхности.
ПодробнееЗона допустимых отклонений
Применяется к отверстию, в которое необходимо вставить штифт, шпильку, винт и т. д. Он контролирует перпендикулярность отверстия в пределах выступа из отверстия и относительно зазора сопрягаемой детали. Выступающая зона допуска простирается над поверхностью детали на функциональную длину штифта, шпильки и винта относительно их сборки с сопрягаемой деталью.
Радиус
Создает зону, определяемую двумя дугами (минимальный и максимальный радиусы). Поверхность детали должна находиться в пределах этой зоны.
Базовый размер
Размер, обычно без допусков, используемый только в информационных целях. Он не регулирует производственные или инспекционные операции. (Дополнительный размер в ISO)
Независимо от размера элемента (RFS)
Условие, при котором должен соблюдаться допуск формы, биения или расположения независимо от того, где элемент находится в пределах допуска размера.
Биение (круговое)
Составное отклонение от заданной формы поверхности вращения детали при полном повороте (360 градусов) детали относительно базовой оси.
ПодробнееИспользуется для обозначения наклона плоских конусов. Этот символ всегда отображается вертикальной ногой слева.
Диаметр сферы
Должен предшествовать значению допуска, если указанное значение допуска представляет сферическую зону. Кроме того, позиционный допуск может использоваться для управления положением сферического элемента относительно других элементов детали.
Символ сферического диаметра предшествует размеру элемента и значению позиционного допуска, чтобы указать сферическую зону допуска.
Сферический радиус
Перед значением размера или допуска.
Передняя поверхность
Цековка и передняя поверхность ранее использовали один и тот же символ. Spotface теперь выглядит как символ цековки с добавлением букв SF.
Квадрат
Используется для обозначения того, что к квадратной форме применяется одно измерение. Символ предшествует размеру без пробела между ними.
Статистическая погрешность
Присвоение допусков связанным компонентам сборки на основе надежной статистики (например, допуск сборки равен квадратному корню из суммы квадратов отдельных допусков). Применяя статистические допуски, можно увеличить допуски отдельных компонентов или уменьшить зазоры между сопрягаемыми деталями. Повышенный допуск или улучшенная посадка могут снизить стоимость производства или улучшить характеристики продукта, но должны использоваться только в том случае, если будет использоваться соответствующий статистический контроль процесса.
Следовательно, следует уделить внимание определению требуемых Cp и/или Cpk или других показателей эффективности процесса.
Прямолинейность
Состояние, при котором элемент поверхности или ось представляет собой прямую линию.
ПодробнееСимметрия
Состояние, при котором элемент (или элементы) расположен симметрично относительно центральной плоскости базового элемента. Больше не доступно в Стандарте 2018 года.
ПодробнееКасательная плоскость
Показана касательная плоскость. Символ размещается в рамке управления элементом с соблюдением указанного допуска.
Целевая точка
Указывает, где в измерении расположена целевая опорная точка на прямой видимости поверхности.
Полное биение
Одновременный комплексный контроль всех элементов поверхности во всех круговых и профильных положениях измерения при повороте детали на 360.
Допуск одностороннего и неравномерно расположенного профиля
Чтобы указать, что профиль допуска поверхности не симметричен истинному профилю, используется этот символ. Первое значение в рамке управления элементом — это общая ширина допуска профиля. Значение, следующее за символом, представляет собой величину допуска в направлении, позволяющем добавить дополнительный материал к истинному профилю.
12.5 Линии и плоскости
Линии и плоскости, пожалуй, самые простые из кривых и поверхностей в трехмерное пространство. Они также окажутся важными, поскольку мы стремимся понимать более сложные кривые и поверхности.
Уравнение линии в двух измерениях: $ax+by=c$; это разумно ожидать, что линия в трех измерениях задается $ax + by +cz = d$; разумно, но неправильно — оказывается, что это уравнение плоскости.
У плоскости нет очевидного «направления», как у линии.
можно связать плоскость с направлением очень полезным способом,
однако: есть ровно два направления, перпендикулярные
самолет.
Любой вектор с одним из этих двух направлений называется нормальный к самолету.
Таким образом, хотя векторов нормали к данной плоскости много, все они
параллельны или антипараллельны друг другу.
Предположим, две точки $\ds (v_1,v_2,v_3)$ и $\ds (w_1,w_2,w_3)$ лежат в плоскости;
тогда вектор $\ds\langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$ параллелен
к самолету; в частности, если этот вектор положить хвостом в
$\ds (v_1,v_2,v_3)$, то его головка находится в точке $\ds (w_1,w_2,w_3)$ и лежит в
самолет. В результате любой вектор, перпендикулярный плоскости,
перпендикулярно $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$. На самом деле, это
Легко видеть, что плоскость состоит из именно те точки
$\ds (w_1,w_2,w_3)$, для которых $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$ равно
перпендикулярно нормали к плоскости, как показано на
рисунок 12.5.1. То есть предположим
мы знаем, что $\langle a,b,c\rangle$ нормальна к плоскости, содержащей
точка $\ds (v_1,v_2,v_3)$. Тогда $(x,y,z)$ лежит в плоскости тогда и только тогда
если $\langle a,b,c\rangle$ перпендикулярно $\ds \langle
x-v_1,y-v_2,z-v_3\rangle$.
В свою очередь, мы знаем, что это правда
именно тогда, когда $\ds \langle a,b,c\rangle\cdot\langle
x-v_1,y-v_2,z-v_3\rangle=0$. Таким образом, $(x,y,z)$ лежит в плоскости, если и
только если
$$\выравнивание{
\langle a,b,c\rangle\cdot\langle x-v_1,y-v_2,z-v_3\rangle&=0\cr
a(x-v_1)+b(y-v_2)+c(z-v_3)&=0\cr
топор+by+cz-av_1-bv_2-cv_3&=0\cr
топор+by+cz&=av_1+bv_2+cv_3.\cr
}$$
Работая в обратном направлении, обратите внимание, что если $(x,y,z)$ — точка, удовлетворяющая
$ax+by+cz=d$ тогда
$$\выравнивание{
топор+by+cz&=d\cr
топор+by+cz-d&=0\cr
a(x-d/a)+b(y-0)+c(z-0)&=0\cr
\langle a,b,c\rangle\cdot\langle x-d/a,y,z\rangle&=0.\cr
}$$
А именно, $\langle a,b,c\rangle$ перпендикулярен вектору с
хвост в $(d/a,0,0)$ и голова в $(x,y,z)$. Это означает, что точки
$(x,y,z)$, удовлетворяющие уравнению $ax+by+cz=d$, образуют плоскость
перпендикулярно $\langle a,b,c\rangle$. (Это не
работать, если $a=0$, но в этом случае мы можем использовать $b$ или $c$ в роли
$а$. То есть либо $a(x-0)+b(y-d/b)+c(z-0)=0$, либо
$a(x-0)+b(y-0)+c(z-d/c)=0$.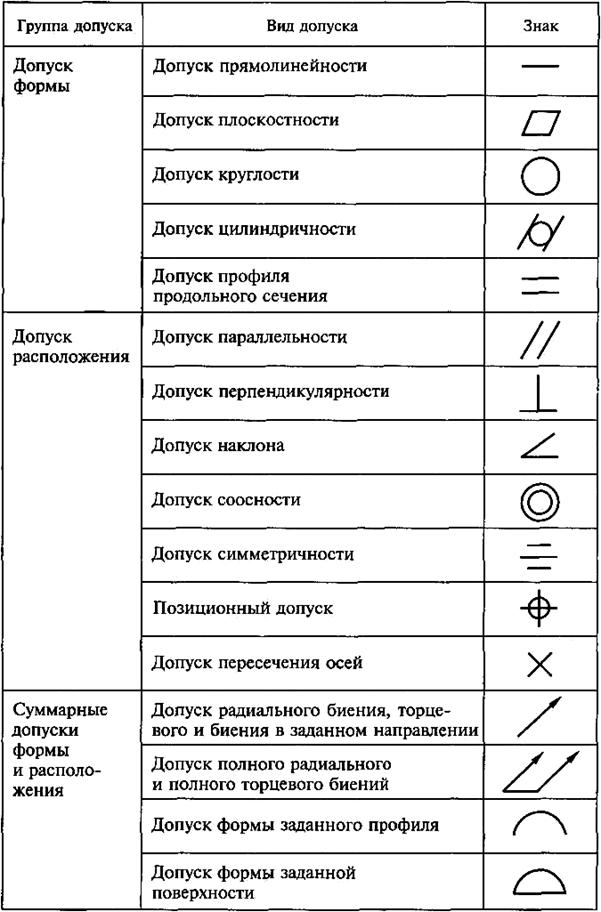
)
Рисунок 12.5.1. Плоскость, определяемая векторами, перпендикулярными нормали.
Таким образом, для вектора $\langle a,b,c\rangle$ мы знаем, что все плоскости перпендикулярные этому вектору, имеют вид $ax+by+cz=d$, и любая поверхность этой формы является плоскостью, перпендикулярной $\langle a,b,c\rangle$.
Пример 12.5.1 Найдите уравнение для плоскости, перпендикулярной $\langle 1,2,3\rangle$ и содержащий точку $(5,0,7)$.
Используя приведенный выше вывод, плоскость $1x+2y+3z=1\cdot5+2\cdot0+3\cdot7=26$. Поочередно, мы знаем, что плоскость равна $x+2y+3z=d$, и чтобы найти $d$, можно подставить известную точку на плоскости, чтобы получить $5+2\cdot0+3\cdot7=d$, поэтому $d=26$. Мы могли бы также записать это просто как $(x-5)+2(y)+3(z-7)=0$, что для много целей прекрасное представление; всегда можно умножить чтобы получить $x+2y+3z=26$. $\квадрат$
Пример 12.5.2 Найдите вектор нормали к плоскости $2x-3y+z=15$.
Одним из примеров является $\langle 2, -3,1\rangle$.
Любой вектор, параллельный или
антипараллельно с этим также работает, например
$-2\langle 2, -3,1\rangle=\langle -4,6,-2\rangle$ также нормальна к плоскости.
$\квадрат$
Нам часто нужно будет найти уравнение для плоскости при определенных условиях. информация о самолете. Хотя иногда может быть немного более короткие пути к желаемому результату, это всегда возможно, и обычно целесообразно использовать данную информацию, чтобы найти нормаль к плоскость и точку на плоскости, а затем найти уравнение в виде выше.
Пример 12.5.3. Плоскости $x-z=1$ и $y+2z=3$ пересекаются по прямой. Найди третья плоскость, содержащая эту прямую и перпендикулярная плоскости $x+y-2z=1$.
Прежде всего заметим, что две плоскости перпендикулярны тогда и только тогда, когда их
нормальные векторы перпендикулярны. Таким образом, мы ищем вектор $\langle
a,b,c\rangle$, то есть
перпендикулярно $\langle 1,1,-2\rangle$. Кроме того, поскольку
желаемая плоскость должна содержать определенную линию, $\langle
a,b,c\rangle$ должны быть перпендикулярны любому вектору, параллельному этому
линия.
Так как $\langle
a,b,c\rangle$ должны быть перпендикулярны двум векторам, мы можем найти это по
вычисление перекрестного произведения двух. Итак, нам нужен вектор, параллельный
к линии пересечения данных плоскостей. Для этого достаточно
знать две точки на прямой. Чтобы найти две точки на этой прямой,
необходимо найти две точки, находящиеся одновременно на двух плоскостях,
$x-z=1$ и $y+2z=3$. Любая точка на обеих плоскостях будет удовлетворять
$x-z=1$ и $y+2z=3$. Легко найти значения для $x$ и $z$
удовлетворяющие первому, такие как $x=1, z=0$ и $x=2, z=1$. Затем
мы можем найти соответствующие значения для $y$, используя второе уравнение,
а именно $y=3$ и $y=1$, поэтому
$(1,3,0)$ и $(2,1,1)$ находятся на прямой
пересечения, потому что оба находятся в обеих плоскостях. Сейчас
$\langle 2-1,1-3,1-0\rangle=\langle 1,-2,1\rangle$ параллелен
линия. Наконец, мы можем выбрать $\langle a,b,c\rangle=\langle
1,1,-2\rangle\times \langle 1,-2,1\rangle=\langle -3,-3,-3\rangle$.
Хотя этот вектор прекрасно подойдет, любой вектор, параллельный или
антипараллельное к нему также будет работать, поэтому, например, мы могли бы выбрать
$\langle 1,1,1\rangle$, который ему антипараллелен.
Теперь мы знаем, что $\langle 1,1,1\rangle$ нормальна к искомой плоскости. и $(2,1,1)$ — точка на плоскости. Поэтому уравнение плоскость равна $x+y+z=4$. В качестве быстрой проверки, поскольку $(1,3,0)$ также находится на линия, она должна быть в самолете; поскольку $1+3+0=4$, мы видим, что это действительно дело.
Обратите внимание, что если бы мы использовали $\langle -3,-3,-3\rangle$ в качестве нормали, мы открыли бы уравнение $-3x-3y-3z=-12$, то мы вполне могли бы заметили, что мы можем разделить обе части на $-3$, чтобы получить эквивалент $x+y+z=4$. $\квадрат$
Итак, теперь мы понимаем уравнения плоскостей; давайте обратимся к линии. К сожалению, это оказывается весьма неудобным представить типичную линию одним уравнением; нам нужно подойти линии по-другому.
В отличие от плоскости, линия в трех измерениях имеет очевидную
направление, а именно направление любого параллельного ему вектора. Фактически
линия может быть определена и однозначно идентифицирована путем предоставления одной точки
на прямой и вектор, параллельный прямой (в одном из двух возможных
направления).
То есть линия состоит именно из тех точек, которые мы можем
достичь, начав с точки и пройдя некоторое расстояние в
направление вектора. Давайте посмотрим, как мы можем перевести это на более
математический язык.
Предположим, что прямая содержит точку $\ds (v_1,v_2,v_3)$ и параллельна
к вектору $\langle a,b,c\rangle$; мы называем $\langle a,b,c\rangle$ a вектор направления для линии.
Если мы поместим вектор $\ds
\langle v_1,v_2,v_3\rangle$ с хвостом в начале координат и головой
в $\ds (v_1,v_2,v_3)$, и если мы поместим вектор $\langle
a,b,c\rangle$ хвостом в $\ds (v_1,v_2,v_3)$, то голова
$\langle a,b,c\rangle$ находится в точке на прямой. Мы можем добраться до через любые указать на линии, выполнив то же самое, за исключением использования
$t\langle a,b,c\rangle$ вместо $\langle a,b,c\rangle$, где $t$
некоторое действительное число. Из-за того, как работает сложение векторов,
точка в начале вектора $t\langle a,b,c\rangle$ — это точка
в начале вектора $\ds\langle v_1,v_2,v_3\rangle+t\langle
a,b,c\rangle$, а именно $\ds (v_1+ta,v_2+tb,v_3+tc)$; видеть
рисунок 12.
5.2.
Рисунок 12.5.2. Векторная форма линии.
Другими словами, когда $t$ пробегает все возможные действительные значения, вектор $\ds \langle v_1,v_2,v_3\rangle+t\langle a,b,c\rangle$ указывает на каждая точка на линии, когда ее конец находится в начале координат. Другой общий способ записать это как набор параметрических уравнений : $$ x= v_1+ta\qquad y=v_2+tb \qquad z=v_3+tc.$$ Иногда полезно использовать эту форму линии даже в двух случаях. размеры; векторная форма прямой на плоскости $x$-$y$ есть $\ds \langle v_1,v_2\rangle+t\langle a,b\rangle$, что совпадает с $\ds \langle v_1,v_2,0\rangle+t\langle a,b,0\rangle$.
Пример 12.5.4. Найдите векторное выражение для линии, проходящей через $(6,1,-3)$ и
$(2,4,5)$. Чтобы получить вектор, параллельный прямой, мы вычитаем $\langle
6,1,-3\rangle-\langle2,4,5\rangle=\langle 4,-3,-8\rangle$. Линия
тогда задается как $\langle 2,4,5\rangle+t\langle 4,-3,-8\rangle$; там
конечно, много других возможностей, таких как $\langle
6,1,-3\rangle+t\langle 4,-3,-8\rangle$.
$\квадрат$
Пример 12.5.5 Определить, совпадают ли прямые $\langle 1,1,1\rangle+t\langle 1,2,-1\rangle$ и $\langle 3,2,1\rangle+t\langle -1,-5,3\rangle$ параллельны, пересекаются или ни один.
В двух измерениях две линии либо пересекаются, либо параллельны; в В трех измерениях линии, которые не пересекаются, могут быть не параллельны. В этом случае, поскольку векторы направления линий не параллельны или антипараллельны, мы знаем, что прямые не параллельны. Если они пересекаются, то должно быть два значения $a$ и $b$, так что $\langle 1,1,1\rangle+a\langle 1,2,-1\rangle= \langle 3,2,1\rangle+b\langle -1,-5,3\rangle$, то есть $$\выравнивание{ 1+а&=3-б\кр 1+2а&=2-5б\кр 1-а&=1+3б\кр }$$ Это дает три уравнения с двумя неизвестными, поэтому может быть, а может и не быть. решение в общем. В этом случае легко обнаружить, что $a=3$ и $b=-1$ удовлетворяет всем трем уравнениям, поэтому прямые пересекаются в точка $(4,7,-2)$. $\квадрат$
Пример 12.5.6. Найти расстояние от точки $(1,2,3)$ до плоскости
$2x-y+3z=5$.
Расстояние от точки $P$ до плоскости является кратчайшим
расстояние от $P$ до любой точки плоскости; это
расстояние, измеряемое от $P$ перпендикулярно плоскости; видеть
рисунок 12.5.3. Это расстояние
является абсолютным значением скалярной проекции
$\ds \overrightarrow{\распорка QP}$
на вектор нормали $\bf n$, где $Q$ — любая точка плоскости.
Легко найти точку на плоскости, скажем, $(1,0,1)$.
Таким образом, расстояние равно
$$
{\ overrightarrow {\ распорка QP} \ cdot {\ bf n} \ over | {\ bf n} |} =
{\ langle 0,2,2 \ rangle \ cdot \ langle 2, -1,3 \ rangle \ over | \ langle 2, – 1,3 \ rangle |} =
{4\over\sqrt{14}}.
$$
$\квадрат$
Рисунок 12.5.3. Расстояние от точки до плоскости.
Пример 12.5.7. Найти расстояние от точки $(-1,2,1)$ до прямой
$\langle 1,1,1\rangle + t\langle 2,3,-1\rangle$. Мы снова хотим расстояния
измеряется перпендикулярно линии, как показано на
рисунок 12.5.4. Желаемое расстояние равно
$$
|\overrightarrow{\ распорка QP}|\sin\theta=
{|\overrightarrow{\strut QP}\times{\bf A}|\over|{\bf A}|},
$$
где $\bf A$ — любой вектор, параллельный прямой.
Из уравнения
линии, мы можем использовать $Q=(1,1,1)$ и ${\bf A}=\langle 2,3,-1\rangle$, поэтому
расстояние
$$
{|\langle -2,1,0\rangle\times\langle2,3,-1\rangle|\over\sqrt{14}}=
{|\langle-1,-2,-8\rangle|\over\sqrt{14}}={\sqrt{69}\over\sqrt{14}}.
$$
$\квадрат$
Рисунок 12.5.4. Расстояние от точки до прямой.
Вы можете использовать Sage для вычисления расстояний до линий и плоскостей, так как это просто включает векторную арифметику, которую мы уже видели. Конечно, вы также можете использовать Sage для выполнения некоторых вычислений, связанных с нахождение уравнений плоскостей и прямых.
Пример 12.5.1 Найдите уравнение плоскости, содержащее $(6,2,1)$ и перпендикулярно $\langle 1,1,1\rangle$. (отвечать)
Пример 12.5.2 Найдите уравнение плоскости, содержащее $(-1,2,-3)$ и перпендикулярно $\langle 4,5,-1\rangle$. (отвечать)
Пример 12.5.3 Найдите уравнение плоскости, содержащее $(1,2,-3)$, $(0,1,-2)$ и $(1,2,-2)$. (отвечать)
Пример 12.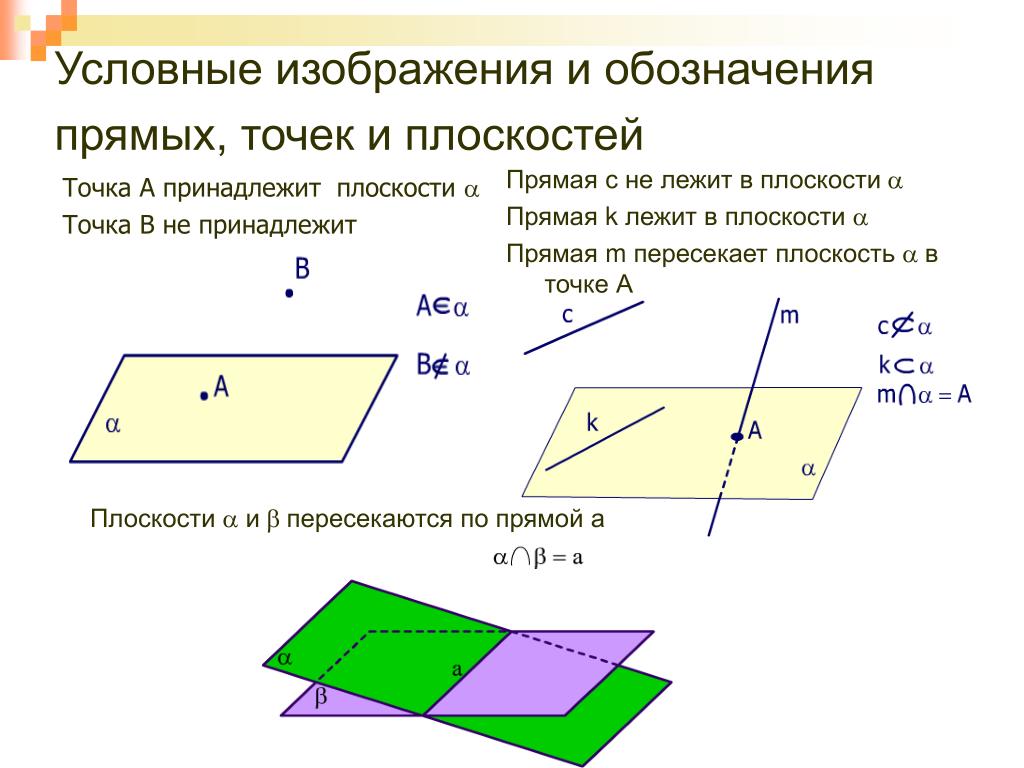
5.4 Найдите уравнение плоскости, содержащее $(1,0,0)$,
$(4,2,0)$ и $(3,2,1)$.
(отвечать)
Пример 12.5.5 Найдите уравнение плоскости, содержащее $(1,0,0)$ и строка $\langle 1,0,2\rangle + t\langle 3,2,1\rangle$. (отвечать)
Пример 12.5.6 Найдите уравнение плоскости, содержащей прямую пересечение $x+y+z=1$ и $x-y+2z=2$ и перпендикулярно плоскость $2x+3y-z=4$. (отвечать)
Пример 12.5.7 Найдите уравнение плоскости, содержащей прямую пересечение $x+2y-z=3$ и $3x-y+4z=7$ и перпендикулярно плоскость $6x-y+3z=16$. (отвечать)
Пример 12.5.8 Найдите уравнение плоскости, содержащей прямую пересечение $x+3y-z=6$ и $2x+2y-3z=8$ и перпендикулярно плоскость $3x+y-z=11$. (отвечать)
Пример 12.5.9 Найдите уравнение прямой через $(1,0,3)$ и $(1,2,4)$. (отвечать)
Пример 12.5.10 Найдите уравнение прямой через $(1,0,3)$ и перпендикулярно плоскости $x+2y-z=1$. (отвечать)
Пример 12.5.
11 Найдите уравнение прямой, проходящей через начало координат
и перпендикулярно плоскости $x+y-z=2$.
(отвечать)
Пример 12.5.12 Найдите $a$ и $c$ так, чтобы $(a,1,c)$ лежало на прямой, проходящей через $(0,2,3)$ и $(2,7,5)$. (отвечать)
Пример 12.5.13 Объясните, как найти решение в пример 12.5.5.
Пример 12.5.14 Определить, являются ли строки $\langle 1,3,-1\rangle+t\langle 1,1,0\rangle$ и $\langle 0,0,0\rangle+t\langle 1,4,5\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.15 Определить, являются ли строки $\langle 1,0,2\rangle+t\langle -1,-1,2\rangle$ и $\langle 4,4,2\rangle+t\langle 2,2,-4\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.16 Определить, являются ли строки $\langle 1,2,-1\rangle+t\langle 1,2,3\rangle$ и $\langle 1,0,1\rangle+t\langle 2/3,2,4/3\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.
5.17 Определить, являются ли строки $\langle 1,1,2\rangle+t\langle
1,2,-3\rangle$ и $\langle 2,3,-1\rangle+t\langle 2,4,-6\rangle$
параллельны, пересекаются или ни то, ни другое.
(отвечать)
Пример 12.5.18 Найдите единичный вектор нормали к каждой из координатных плоскостей.
Пример 12.5.19 Покажите, что $\langle 2,1,3 \rangle + t \langle 1,1,2 \rangle$ и $\langle 3, 2, 5 \rangle + s \langle 2, 2, 4 \rangle$ одинаковы линия.
Пример 12.5.20 Дайте краткое описание каждого из следующих процессов:
а. Даны две различные точки, найти прямую, которая проходит через них.
б. Даны три точки (не все на одной прямой), найдите плоскость что проходит через них. Зачем нужна оговорка, что не все точки лежат на одной прямой?
в. Даны прямая и точка, не лежащие на этой прямой, найти плоскость, на которой содержит их обоих.
д. Даны плоскость и точка, не лежащие на плоскости, найти прямую,
перпендикулярен плоскости, проходящей через данную точку.
Пример 12.5.21 Найдите расстояние от $(2,2,2)$ до $x+y+z=-1$. (отвечать)
Пример 12.5.22 Найдите расстояние от $(2,-1,-1)$ до $2x-3y+z=2$. (отвечать)
Пример 12.5.23 Найдите расстояние от $(2,-1,1)$ до $\langle 2,2,0\rangle+t\langle 1,2,3\rangle$. (отвечать)
Пример 12.5.24 Найдите расстояние от $(1,0,1)$ до $\langle 3,2,1\rangle+t\langle 2,-1,-2\rangle$. (отвечать)
Пример 12.5.25 Найдите расстояние между линиями $\langle 5,3,1\rangle+t\langle 2,4,3\rangle$ и $\langle 6,1,0\rangle+t\langle 3,5,7\rangle$. (отвечать)
Пример 12.5.26 Найдите расстояние между линиями $\langle 2,1,3\rangle+t\langle -1,2,-3\rangle$ и $\langle 1,-3,4\rangle+t\langle 4,-4,1\rangle$. (отвечать)
Пример 12.5.27 Найдите расстояние между линиями $\langle 1,2,3\rangle+t\langle 2,-1,3\rangle$ и $\langle 4,5,6\rangle+t\langle -4,2,-6\rangle$. (отвечать)
Пример 12.5.28 Найдите расстояние между линиями
$\langle 3,2,1\rangle+t\langle 1,4,-1\rangle$ и
$\langle 3,1,3\rangle+t\langle 2,8,-2\rangle$.