Разное

Что такое наклон: Ejercicio de Угловой коэффициент прямой

alexxlab 17.02.2023 Нет комментариев

Содержание

Функция НАКЛОН – Служба поддержки Майкрософт

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование функции НАКЛОН в Microsoft Excel.

Описание

Возвращает наклон линии линейной регрессии для точек данных в аргументах известные_значения_y и известные_значения_x. Наклон определяется как частное от деления расстояния по вертикали на расстояние по горизонтали между двумя любыми точками прямой; иными словами, наклон — это скорость изменения значений вдоль прямой.

Синтаксис

НАКЛОН(известные_значения_y;известные_значения_x)

Аргументы функции НАКЛОН описаны ниже.

  • Известные_значения_y    Обязательный. Массив или диапазон ячеек, содержащих зависимые числовые точки данных.

  • Известные_значения_x    Обязательный. Множество независимых точек данных.

Замечания

  • Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.

  • Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.

  • Если аргументы известные_значения_y и известные_значения_x пусты или количество содержащихся в них точек не совпадает, функция НАКЛОН возвращает значение ошибки #Н/Д.

  • Уравнение наклона линии регрессии имеет следующий вид:

    где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).

  • Основной алгоритм, используемый в функциях НАКЛОН и ОТРЕЗОК, отличается от основного алгоритма функции ЛИНЕЙН. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных.

    Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то справедливо указанное ниже.

    • Наклон и ОТОКП возвращают #DIV/0! ошибку “#ВЫЧИС!”. Алгоритм НАКЛОН и ОТОКП предназначен для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.

    • Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм, используемый в функции ЛИНЕЙН, предназначен для возврата правдоподобных результатов для коллинеарных данных, а в этом случае может быть найдено по меньшей мере одно решение.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные

Известные значения y

Известные значения x

02.01.1900

6

03. 01.1900

5

09.01.1900

11

01.01.1900

7

08.01.1900

5

07.01.1900

4

05. 01.1900

4

Формула

Описание

Результат

=НАКЛОН(A3:A9;B3:B9)

Наклон линии линейной регрессии для точек данных в диапазонах A3:A9 и B3:B9.

0,305556

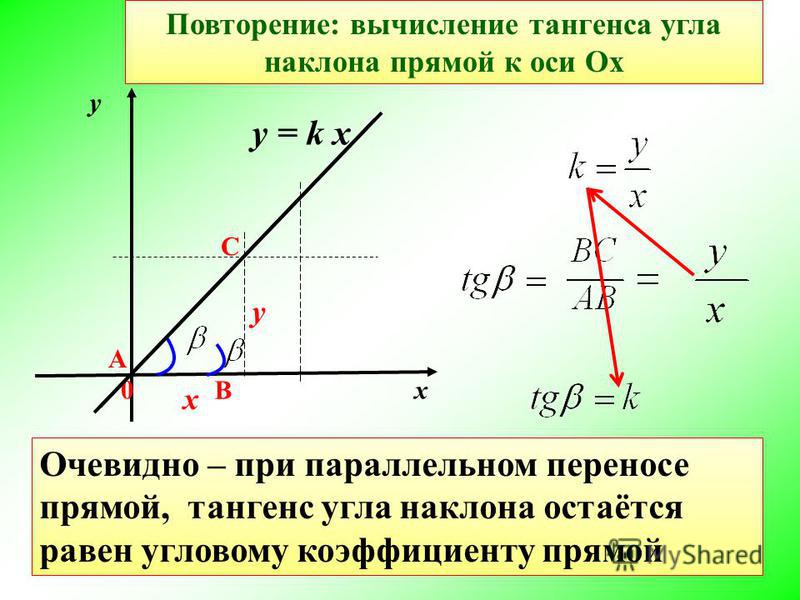
Наклон линии (крутизна)

      Наклон линии (крутизна)
Предствим, что частица движется вдоль участка не вертикальной прямой из точки p1

( x1,y1 ) к точке p1( x1,y1 ). Вертикальное изменение y2 – y1 называется подъемом, а горизонтальное изменение x2 – x1 – расстоянием.

      ОПРЕДЕЛЕНИЕ
Если P(x1, y1) и P(x2, y2) есть точками на невертикальной прямой, тогда крутизна m прямой определяется как:

Не имеет значение, какая точка называется P1 и какая точка называется P2
      Slope of  P1P2

= (y2

– y1)/(x2 – x1)

= -(y1 – y2)/[-(x1 – x2)]

= (y1 – y2)/(x1 – x2) = Крутизна P1P2

Любые две различные точки на не вертикальной прямой могут быть использованы для расчета крутизны (наклона) прямой. Для измерения наклона, мы обычно двигаемся слева направо, когда измеряем дистанцию, пройденную горизонтально.
Из-за этого, иногда понятие падения подменяется подъемом!

      Пример
В каждой части найдите наклон линии, проходящей через
          (A)     (6, 2) и (9, 8)

          (B)     (2, 9) и (4, 3)
          (C)    (-2, 7) и (5, 7)

Решение:
Мы знаем, что наклон линии, проходящей через две точкиP1(x1, y1) иp1(x1, y1) , определяется как
m= (y2 – y1)/ (x2 – x1)
Отсюда
    a) m= (8 – 2)/(9 – 6) = 6/3 = 2
На координатной плоскости xy

Подобным образом
    b) m= (3 – 9)/(4 – 2) = -6/2 = -3
На координатной плоскости xy

Также
    c) m= (7 -7)/[5 – (-2)] = 0/7 = 0
На координатной плоскости xy

      Определение (Угол наклона)
Для прямой L не параллельной к оси абсцисс, угол наклона есть наименьший углом φ, измеренный против часовой стрелки от направления положительная оси х к L.

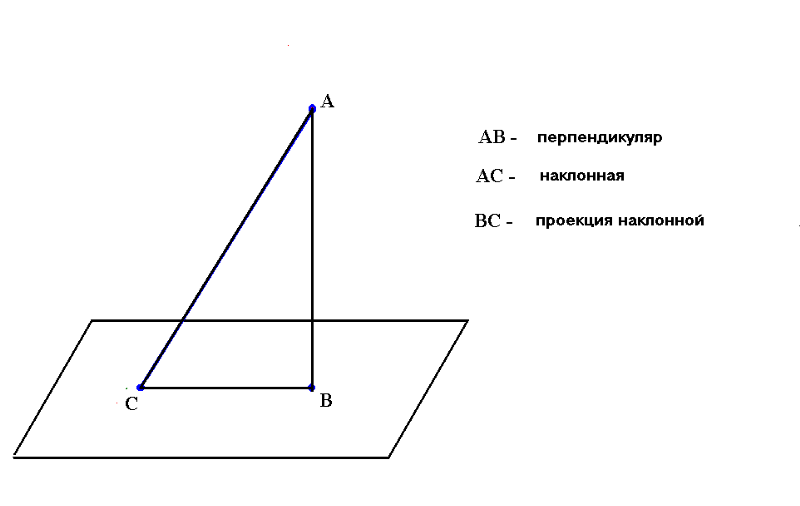
Для прямой, параллельной оси x, мы берём φ = 0
Как показано на следующих рисунках.
       

Если m есть наклоном прямой, тогда
m = rise/run
    = скорость изменения y относительно к x

      ТЕОРЕМА
Для не вертикальной прямой наклон m и угол наклона φ связаны отношением
            m = tan φ

      Пример:
Найдите угол наклона для прямой с наклоном m = 1 и угол наклона для прямой с наклоном m = -1

      Solution:
  Если m=1 tan φ = 1, и поэтому φ = π/4 = 45°

  Если m=-1 tan φ = -1, так как 0 φ = 3π/4 = 135°

      Теорема Пусть L1 и L2 есть прямыми с наклонами m1 и m2, соответственно
  (a)   Прямые параллельны тогда и только тогда       m1 = m2
  (b)   Прямые параллельны тогда и только тогда       m1m2 = -1

      Доказательство: (a)
Если L1 и L2 не являются вертикальными прямыми, тогда их углы наклона φ1 и φ2 равны.
            φ1 =φ2
Так,
    m1 = tanφ1 = tanφ2 = m2

И наоборот, если два наклона линий равны, т.e.
        M1 = M2
⇒     tan(φ1) = tan(φ2)
⇒         φ1 = φ2
То есть, прямые параллельны.

(b) Предположим, что φ12
Тогда, обращаясь к рисунку
m1 = tanφ1 = c/h

m2 = tanφ2 = -h/c

Доказательства обратного предлагается сделать в качестве упражнения.

      TЕОРЕМА
Вертикальная прямая через (a, 0) и горизонтальная прямая через (0, b) представлены, соответственно, уравнением
x = a и y = b
      ТЕОРЕМА
Прямая, проходящая через P1(x1, y1) и имеющая наклон m, выражается уравнением
            y – y1 = m(x – x1)
      ТЕОРЕМА
Прямая с пересечением оси y в b и наклоном m выражается уравнением
            y = mx + b

Что такое уклон? Формула, кривые и касательные

Что такое уклон? Содержание (Нажмите, чтобы перейти к этому разделу):

  1. Определение
  2. «Подъем над бегом»
  3. Формула прямой линии
  4. Найдите наклон с помощью алгебры

Дополнительные темы:

  1. Наклон кривой
  2. Наклон касательной линии (с использованием определения предела)
  3. Что такое наклонное поле?
  4. Анализ устойчивости откосов

Слово «наклон» в математике имеет примерно то же значение, что и в повседневном языке:

«…поверхность, один конец или сторона которой находится на более высоком уровне, чем другой; поднимающаяся или опускающаяся поверхность».

При использовании в математике он немного более определен; это число, которое описывает как направление (положительное или отрицательное) , так и крутизну линии. Обычно его обозначают буквой м .

Неофициально наклон линии определяется броской фразой « подъем над пробегом ». Это работает с любым сегментом любой длины для любой прямой линии:

  1. Найдите подъем (длину сегмента по оси Y): Рост (длину вертикальной синей линии) в приведенном выше фото 4.
  2. Найдите «пробег» (длину сегмента по оси x): Прогон (длина горизонтальной синей линии) равен 2.
  3. Разделить рост (шаг 1) на длину пробега (шаг 2): 4/2 = 2,

Наклон для этого примера равен 2.

Формула для прямой линии :

Где:

  • b = точка пересечения y (где график пересекает ось y),
  • м = уклон (т.е. насколько крута линия),
  • х = переменная.

Уравнение прямой линии (формально называемое «линейным уравнением») довольно просто использовать, если вам дан набор точек (пример 1). Вас также могут спросить, каков наклон для чего-то вроде y = -9.(пример 2) или x = -2,5 (пример 3). Хотя оба они являются уравнениями (и вы можете подумать, что y = mx + b поможет), на самом деле вам нужна формула, чтобы представить ответ.*
Примеры :

  1. Наклон точек (2,1) и (4,2) равно 1/2, потому что: (y 2 – y 1 ) / (x 2 – x 1 ) = (2 – 1) / (4 – 2) = 1 /2.
  2. Наклон y = 9 равен нулю . График y = 9 параллелен оси x и является плоским (т.е. он вообще не растет и не падает). Вы может использовать формулу , чтобы вычислить это, выбрав пару случайных значений x (я выберу 2 и 3): – x 1 )
    = (9 – 9)/(2 – 1) = 0 / 1 = 0.
    Поскольку значения y постоянны и всегда будут равны нулю при вычитании (т. е. 10 – 10, 4 – 4, -3 – -3), наклон линии с уравнением y = «любое число» всегда будет равен нулю.
  3. Наклон x = 5 не определен . Любая строка с уравнением x = «любое число» будет неопределенной , потому что посмотрите, что произойдет, если вы подставите пару точек (любых случайных точек) в формулу:
    m = (2 – 1) / (5 – 5) = 1 / 0 = деление на ноль не определено.

*Тем не менее, технически вы можете просто запомнить, что уравнения вида y = «любое число» имеют наклон, равный нулю, а x = «любое число» имеет неопределенный наклон.

Основная формула линейного уравнения: y = mx + b, где «m» — наклон. Если вам дана формула и вам нужно найти m, вам может потребоваться:

  • Посмотрите на формулу, чтобы найти ее (пример 1),
  • Примените немного алгебры, чтобы получить уравнение в правильной форме (пример 2).

Примеры :

  1. Наклон y = 2x + 5 равен 2.
  2. Наклон 3y – 9x = 12 равен 3, потому что если мы переформулируем формулу так, чтобы она выглядела как y = mx + b, мы получим:
    Прибавив 9x к обеим сторонам: 3y = 9x + 12. сторон): у = 3х + 4,

Совет : если перед x ничего нет (т.е. y = x + 2), наклон равен 1, потому что 1*x = x.

2. Базовая формула уклона: m = подъем/спуск = (y 2 – y 1 ) / (x 2 – x 1 ).

Основное различие между наклоном прямой линии и наклоном кривой заключается в том, что наклон прямой линии остается постоянным, тогда как наклон кривой изменяется между точками.

Как определить наклон кривой, если значения постоянно меняются? Мы можем сделать это, используя касательную линию. А Касательная линия — это прямая линия, которая касается построенной кривой в одной точке. Эта точка известна как точка касания .


Касательная — это маленькая красная линия в верхней части рисунка. Обратите внимание, как он касается изогнутой линии в одной точке.


Формула для наклона кривой

Наклон линейного уравнения можно найти по формуле: y = mx + b. При работе с изогнутой линией, где наклон меняется, вы не можете использовать ту же формулу. Вы должны разделить изменение значений y на изменение значений x, представленное как:

m = изменение y/изменение x

Чтобы использовать эту формулу для определения наклона кривой, выберите две точки для подстановки в формулу. Давайте посмотрим на пример.

Пример вопроса: Найдите м в точке (9, 3).
На графике выше касательная снова нарисована красным. Касательная касается кривой в точке (2.3, 5). Как только мы получим точку касательной, останется только подставить значения в формулу.

м = (9-5)/(3-2,3) = 4/0,7 = 5,71.

Таким образом, наклон кривой в точке (9, 3) равен 5,71.

6. Как найти наклон касательной с помощью определения предела

Существует несколько способов найти наклон касательной. Обычный способ — взять производную — она равна наклону касательной в любой точке. Однако, если вас попросят использовать «определение предела», скорее всего, вы еще не рассмотрели, как взять производную в своем классе. Формальное определение предела можно использовать для нахождения наклона касательной:
Если точка P(x 0 ,y 0 ) находится на кривой f , то касательная в точке P имеет наклон, определяемый формулой:
M tan = lim ч → 0 f(x 0 + h) – f(x 0 )/h .

Пример вопроса: Найдите наклон касательной к кривой f(x) = 2x 2 + 3x – 4, проходящей через точку P(-1, 5).

Шаг 1: Замените «x» в исходной функции на x + h в первой части определения предела:
m tan = lim h→0 [2 ( x + h ) 2 ] + 3(x + h) + 4]

Шаг 2: Вычтите исходную функцию и разделите на h (все, что вы здесь делаете, это завершаете определение предела):
m tan = lim h→0 [2 ( x + h ) 2 + 3(x + h) – 4] – [2x 2 + 3x – 4 ] / h

Шаг 3: Решить с помощью алгебры . Вся цель следующих шагов состоит в том, чтобы удалить «h» из знаменателя, чтобы предотвратить деление на ноль:

  1. ФОЛЬГА первая часть, (x + h) 2 :
    m тангенс = lim h →0 [2(x 2 + 2hx + h 2 ] + 3(x + h) – 4] – [2x 2 + 3x – 4 ] / h
  2. Умножить 3(x + h):
    m tan = lim h→0 [2(x 2 + 2hx + h 2 ] + 3x + 3h – 4] – [2x 2 + 3x – 4 ] / ч
  3. Распределить отрицательный знак
    m tan = lim → 0 [2(x 2 + 2hx + h 2 ] + 3x + 3h – 4] – 2x 9002 + 4 2 / ч
  4. Распределить ведущий 2:
    m tan = lim h→0 [2x 2 + 4hx + 2h 2 + 3x + 3h – 4 – 2x 2 9] ч
  5. Условия отмены (-3x, -2x 2 , -4)
    m tan = lim h→0 [4hx + 3h 2 + 3h ] / h
  6. Фактор «h»:
    m tan = lim h→0 h (4x + 2h + 3) / h
    = lim h→0 4x + 2h + 3
  7. Установите « 2h » на ноль (поскольку вы берете предел, «h» не имеет значения). Другими словами, удалите его:
    = lim h→0 4x + 3

Это дает вам функцию наклона касательной.

Шаг 4: Введите точку в функцию :
м тангенс = 4 (-1) + 3 = -1
Наклон касательной равен -1.

Вот и все!
Вернуться к началу

Поле наклона (иногда называемое полем направлений ) представляет решения дифференциального уравнения первого порядка скалярной функции. Ряд засечек указывает наклон. Термины поле наклона и векторное поле иногда используются для обозначения одного и того же, но есть важное отличие: все засечки в поле наклона имеют одинаковую длину; Метки в векторных полях различаются по длине в зависимости от величины вектора.

По сути, поле наклона содержит серию коротких двунаправленных линий, каждая из которых имеет длину в одну единицу и каждая из которых показывает касательную к кривой функции в своих центральных точках.

Поля наклона также иногда называют полями направления, особенно если векторы содержат стрелки направления.

На изображении ниже показано поле наклона dy/dx = x 2 – x – 2. Три функции представлены разными цветами:

  • Синий: y = (x 3 /3)-(x 2 /2) – 2х + 4,
  • Красный: у = (х 3 /3)-(х 2 /2) – 2х,
  • Бирюза: y = (x 3 /3)-(x 2 /2) -2x – 4.


Применение полей уклонов

Поля уклонов даже очень сложных производных могут быть созданы компьютером быстро и без усилий, поэтому они часто используются в качестве первого шага в понимании проблемы, прежде чем будет принято решение о процедурах поиска точное решение. Они дают хорошее визуальное представление о проблеме и позволяют увидеть поведение решения в долгосрочной перспективе.

Их также можно использовать в качестве руководства для определения возможных решений. В тех случаях, когда у нас нет фактической производной на руках, они могут использоваться компьютерами для генерации числовых решений с помощью таких процедур, как метод Эйлера или методы Рунге-Кутты.

Анализ устойчивости склонов – это изучение факторов устойчивости и, следовательно, безопасности как естественных, так и искусственных склонов.

Устойчивость склона обычно определяется как устойчивость уклона к «разрушению», когда разрушение представляет собой обрушение или скольжение. Анализ обычно включает работу с двумя типами уравнений: уравнениями равновесия, применяющими физику к полевым условиям, и определяющими законами (то есть законами, характерными для конкретного вещества), которые описывают поведение почвы.

Типы анализа

Анализ устойчивости откосов проводится различными способами, но, вероятно, наиболее часто используется так называемый анализ предельного равновесия . В этом анализе изучается равновесие между градиентом и поверхностью скольжения (это может быть прямая линия, логарифмическая спираль или дуга окружности). Рассчитываются касательные напряжения (τ), рассчитывается доступное сопротивление (τ f ) и выводится «коэффициент запаса прочности», F= τ ф /т.

Некоторые методы анализа работают со склоном как с твердым телом, но большинство делят его на срезы и рассчитывают равновесие каждого отдельного среза. Это имеет то преимущество, что позволяет аналитику работать с неоднородными поверхностями.

Применение

Анализ устойчивости откосов играет важную роль в проектировании и проектировании любых архитектурных сооружений с наклонными поверхностями, включая насыпи автомагистралей и горные дороги. Это также имеет решающее значение для предотвращения ущерба от землетрясений и позволяет лесникам и ландшафтным дизайнерам определять опасные зоны, которые могут быть склонны к оползням и лавинам.

Ссылки

Катанзарита, Филиппо. Анализ устойчивости
Получено с https://www.geostru.eu/slope-stability-analysis/ 3 апреля 2018 г.
Инженерный корпус армии США. Инженерное руководство.
Получено с http://www.civil.utah.edu/~bartlett/CVEEN5305/Handout%2010%20-%20EM_1110-2-1902.pdf 3 апреля 2018 г.

Что такое уклон? Ссылки

Баркер, Кристофер А. Теоретическое введение в поля наклона. Компьютерная лаборатория Центра обучения математике и естественным наукам. Колледж Сан-Хоакин Дельта. Получено с http://calculuslab.deltacollege.edu/ODE/7-1/7-1-0-h.html 6 апреля 2019 г..
Кан, Д. Сдача экзаменов AP Calculus AB и BC.
Ларсон и Эдвардс. Исчисление.
Шварц, Кен. Дифференциальные уравнения: генератор поля наклона. GeoGebra Получено с https://www.geogebra.org/m/MJbBarpr 6 апреля 2019 года. «Что такое уклон? Формула, кривые и касательные» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/calculus-definitions/what-is-a-slope/

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Форма пересечения уклона: определение, примеры | Turito

Форма наклона-пересечения входит в число четырех других методов определения уравнения любой прямой линии. Прямые линии обычно представляются как y = mx+c. Это стандартное уравнение прямой определяет, что переменные x и y имеют максимальную степень единицы. Это означает, что x = x1 и y = y1.

Кроме того, это подтверждает, что форма наклона-отрезка может быть применена только к линейным уравнениям. Вы должны быть знакомы с линейными уравнениями с двумя переменными. Следует знать, что график таких уравнений представляет собой прямую линию. Вы также должны быть уверены в том, что такое y-пересечение, x-пересечение и характеристики наклона линейных уравнений.

Если вы попытаетесь решить уравнение типа x = 2a 3 + y, это может оказаться немного сложным, и есть вероятность получить ошибки в форме пересечения наклона.

Остальные четыре формы или метода решения линейного уравнения перечислены ниже:

  • Форма пересечения наклона
  • Форма перехвата
  • Форма двухточечная
  • Форма точечного откоса

 В этой статье вы узнаете о форме пересечения наклона, что такое форма пересечения наклона, уравнение формы пересечения наклона, как найти форму пересечения наклона, как написать уравнение в форме пересечения наклона и -форма пересечения линейного уравнения.

Что такое форма пересечения наклона?

Форма пересечения наклона прямой линии является одним из наиболее частых способов описания ее уравнения. Представьте, что вам дан наклон линии, и вы знаете, что эта линия пересекает ось Y в какой-то точке декартовой плоскости. В таких случаях разумно использовать форму пересечения наклона.

Вы можете разделить форму пересечения наклона на два понятия:

  • Наклон линии: Отношение разницы между координатами по оси Y к разнице между координатами по оси X.
  • ‘y’ Intercept: точка на оси y, где линия с определенным наклоном пересекается или пересекается, является точкой пересечения y.

Примечание: Координаты точки пересечения y всегда (0, y). Это связано с тем, что линия, уравнение которой необходимо определить, всегда пересекает ось Y в точке x = 0.

Формула пересечения наклона

Уравнение пересечения наклона записывается следующим образом: x, y — координаты x и y,

м — наклон линии, а

b — точка пересечения с осью Y.

Что такое форма пересечения наклона прямой линии?

Внимательно посмотрите на приведенный ниже рисунок. Вы увидите прямую линию «AB», которая проходит через 1-й квадрант системы координат и пересекает ось y в точке C. Координаты этой точки C, скажем, C (0, y). Кроме того, если мы видим линию «ABC», она наклонена на несколько градусов от оси x. Это наклон заданной прямой. Это единственное, что нам нужно, чтобы найти уравнение прямой линии, используя форму пересечения наклона.

Примечание. Если координаты линий удовлетворяют или согласуются с уравнением, то координаты правильные. Если координаты не удовлетворяют уравнению, то они не являются координатами этой линии.

Уравнение формы пересечения наклона 

Теперь мы подтверждаем, что форма пересечения наклона прямой линии — это аккуратный и упрощенный способ найти уравнение прямой. В математике формула пересечения наклона задается как:

y = mx + k, или вы можете использовать любую переменную вместо этих терминов, но помните, что:

  1. ‘y’ и ‘x’ всегда остаются неизменными. Они являются причиной того, что этот термин является уравнением.
  2. ‘м’ определяется как наклон линии, а
  3. «k» — это точка пересечения «y», о которой говорилось ранее.
Некоторые примеры формы пересечения наклона

Чтобы упростить все теоретические знания, упомянутые выше, давайте рассмотрим некоторые примеры формы пересечения наклона и научимся писать уравнение в форме пересечения наклона.

Пример 1: Наклон линии XY равен (-1), а точка пересечения с осью y равна (10). Что такое уравнение прямой?

Ответ: y = (-1) x + 10.

Пример 2: Наклон линии XY равен (7), и линия проходит от начала координат. Что такое уравнение прямой?

Ответ: y = (7) x + 0 => y = 7x {Поскольку, когда линия проходит от начала координат, точка пересечения x и y равна (0,0)}

Пример:  

Если точка пересечения с осью y равна 8, а наклон равен 3, найдите уравнение прямой линии.

Решение:  

Шаг 1: Определите значения.

b = 8

м = 3

Шаг 2: Постройте уравнение формы уклона и введите значения.

y = mx + b

y = 3x + 8

Пример:  

Используя форму точки пересечения, определите уравнение прямой линии с наклоном 1/7 и точкой пересечения с точкой ( 0, -9).

Решение:  

Чтобы найти уравнение заданной прямой, выполните следующие действия: 

Дано: наклон линии m = 1/7.

Точка пересечения линии по оси y равна (0, b) = (0, -9) b = -9.

Уравнение данной линии вычисляется по формуле пересечения наклона.

y = mx + b 

y = (1/7) x – 9 

Ответ: Уравнение данной прямой: y = (1/7) x – 9. 

Как найти наклон линия?

Эта концепция может показаться вам сложной, но как только вы ее поймете, вы преуспеете в нахождении наклонов прямых линий.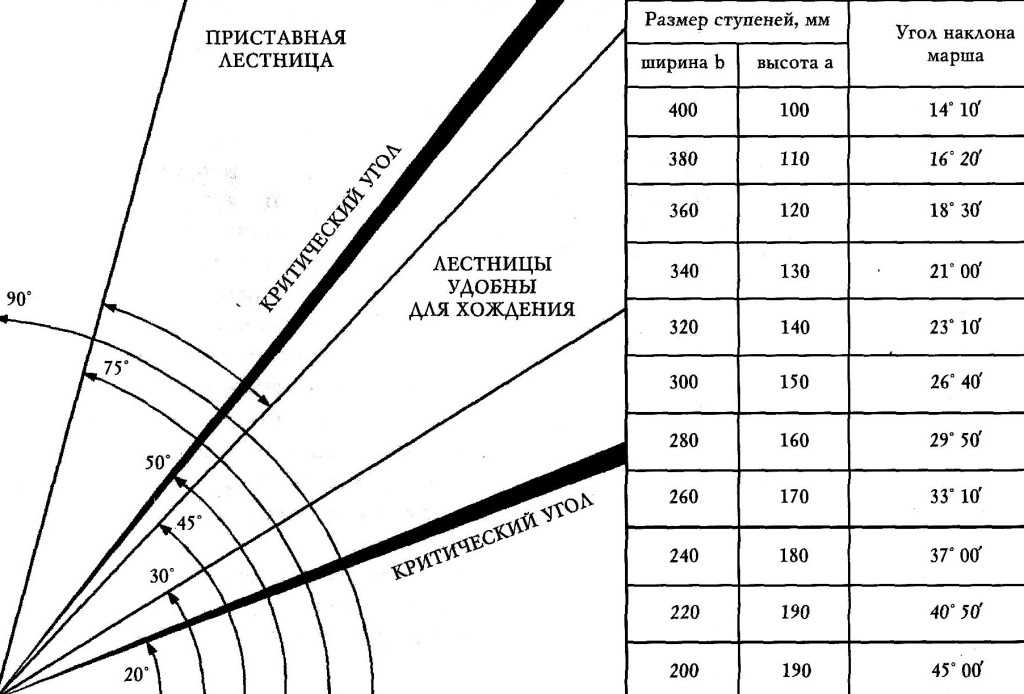

Метод 1: Если вы знаете, под каким углом линия наклонена к оси X, вы можете найти наклон с помощью простой тригонометрии. Предположим, что наша линия наклонена под углом ‘a’ от оси x, тогда

Наклон ‘m’ = tan (a) 

Метод 2: Если координаты двух точек на одной линии заданы, мы можем легко найти наклон, найдя отношение разности координат по оси y к разности координат по оси x. Например: предположим, что точки (x, y) и (x1, y1) лежат на одной линии, тогда 

Наклон ‘m’ = (y – y1) / (x – x1)

Для более глубокого понимания этого понятия см. формулу пересечения наклона и ее вывод ниже.

Вывод формулы для формы пересечения наклона

Предположим, произвольная точка на линии: A (x, y). Кроме того, давайте рассмотрим, что наклон линии равен «m», и эта линия пересекает вертикальную ось (ось y) в точке k, так что точка C равна (0, k). См. схему для лучшего понимания.

Используя формулу для нахождения наклона, когда даны две точки, мы имеем:

m = (y – y1) / (x – x1)

m = (y – k) / (x – 0)

m (x – 0) = y – k

mx = y – k

y = mx + k

Это общее уравнение для прямой линии, которое включает наклон и точку пересечения с осью y. Форма пересечения наклона – это название, данное этому типу линейного уравнения. В результате создается формула пересечения наклона. Теперь вы знаете, как написать форму пересечения наклона.

Важно отметить, что формулу пересечения наклона нельзя использовать для получения уравнения вертикальной линии. Это потому, что вертикальная линия не имеет точки пересечения с точкой Y.

Уравнение прямой линии с использованием формы пересечения наклона

Два необходимых параметра, а именно, наклон «m» линии и точка пересечения с осью y «k», используются для определения уникальности любой линии.

Процедуры для определения уравнения линии с использованием формы пересечения наклона описаны ниже.

Шаг 1: Запишите точку пересечения оси Y, «k», и наклон прямой, «m». формула, чтобы найти его. (Формулы наклона указаны выше в статье) 

Шаг 2: Используйте формулу пересечения наклона для решения задачи: y = MX + k.

  Пример: Линия наклонена под углом 45° к оси x и проходит через точку (0, 10). Найдите уравнение прямой.

Ответ: Имеем, m = tan 45º = 1

Таким образом, уравнение этой прямой: y = mx + k

y = (1) x + (10)

y = x − 10

Не слишком ли проста для вас форма линейного уравнения, состоящая из наклона и пересечения?

Теперь, когда мы рассмотрели все теоретические аспекты этой темы, давайте рассмотрим несколько достойных примеров, чтобы лучше понять концепции этой статьи.

Примеры формы пересечения наклона

Пример 1: Учитывая, что наклон линии равен 1/2, и она пересекает ось Y в точке (0, -3). Найдите уравнение прямой.

Решение: Нам дан наклон ‘m’ = 1/2,

Координаты точки на оси Y, где линия пересекает = (0, -3) 

Следовательно, k = -3

Уравнение прямой => y = mx + k,

y =(1/2) x + (-3)

y = x/2 – 3

Ответ: Уравнение прямой y = x/2 – 3.

Пример 2: Найдите уравнение, используя формулу пересечения наклона горизонтальной линии, которая пересекает ось y в точке (0, 8). Реши это.

Решение: Нам известно, что линия горизонтальна, что означает, что угол наклона «а» равен 0.

Таким образом, tan (0) = 0

Координаты точки на оси Y, где линия пересекает = (0, 8) 

Следовательно, k = 8

Уравнение прямой => y = mx + k,

y = 0 x + (8)

y = 8

Ответ: Уравнение прямой y = 8. Это подводит итог статьи о форме пересечения наклона, как найти форму пересечения наклона, как написать уравнение в форме пересечения наклона , и форма пересечения наклона линейного уравнения. Если у вас все еще есть сомнения и вы думаете, что упустили некоторые концепции, вы можете вернуться к этой статье и найти ответы на свои вопросы в подробно разработанных параграфах. Более того, не забывайте изучать новые концепции и регулярно их практиковать.

Часто задаваемые вопросы

1. Что такое форма пересечения наклона в математике?

Ответ.  В математике форма пересечения наклона – это способ записи уравнения для прямой в форме y = mx + b. m представляет собой наклон линии, а b представляет собой точку пересечения с осью y. Форма пересечения наклона используется, когда вы хотите найти либо точку на линии, либо найти y, если вы знаете x.

2. Что такое уравнение формы пересечения уклона?

Ответ.  Уравнение формы пересечения наклона: y = mx + b. Это уравнение используется для нахождения наклона и точки пересечения линии по оси Y. Наклон показывает, насколько быстро линия меняется от точки к точке, а b представляет собой начальную точку линии (т. е. место ее пересечения с осью Y).

3. Как найти форму пересечения наклона?

Ответ.  Чтобы найти форму Slope Intercept, вам нужно знать, что такое уклон линии. Наклон линии можно рассчитать по формуле: наклон = (y2 – y1)/(x2 – x1)

4. Что такое формула пересечения наклона?

Ответ.  Формула точки пересечения наклона — это простое уравнение, которое можно использовать для определения наклона и точки пересечения линии по оси Y.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *