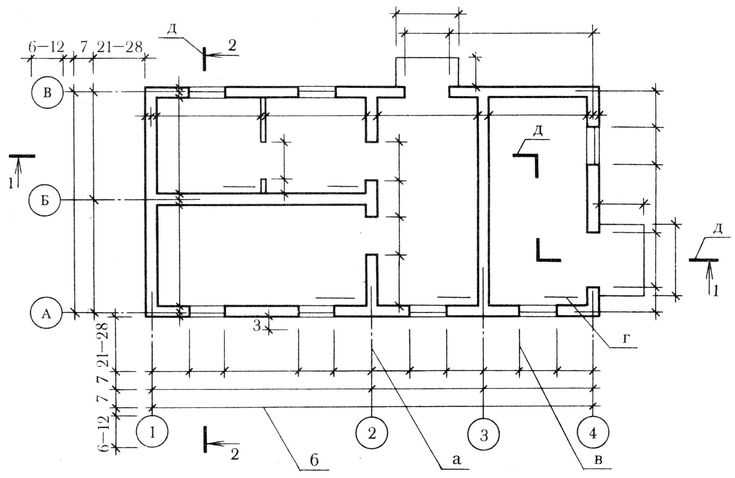
1 .5 Нанесение размеров гост 2.303.68
Стандарт устанавливает_______________________________________________________________
______________________________________________________________________________________
Размеры указываются__________________________________________________________________
_____________________________________________________________________________________
Размерные числа наносятся_____________________________________________________________
_____________________________________________________________________________________
Выносные линии должны выходить за концы стрелок размерной линии на … мм |
Каждый размер наносят________________________________________________________________
Нанести
размеры на выполненных чертежах в
соответствии с ГОСТ 3.
7
1 .6 Масштабы гост 2.302 – 68
Масштабом называется_________________________________________________________________
______________________________________________________________________________________
Стандарт устанавливает следующие масштабы
Уменьшения | |
Натуральная величина | |
Увеличения |
Начертить чертеж прокладки, считая размер изображенной клетки 5 мм, и нанести размеры, необходимые для ее изготовления. |
8
8
1 .7 Геометрические построения
Выполнить указанные построения
Разделить отрезок на равные части: а) на 4 части б) на 5 частей | Разделить угол на равные части а ) на 2 части б) на 3 части |
П
роведите
перпендикуляр к прямой через точки А
и В. | Проведите прямую параллельную данной. |
Найдите центр окружности. | Проведите окружность через три точки. |
Постройте треугольник, равный данному. | Постройте многоугольник, равный данному. 9 |
9
9
9
1 10 .8 Деление окружности на равные части. Построение правильных многоугольников
Впишите в окружности ø50 равносторонние многоугольники.
а) три равные части | б) четыре равные части |
в) шесть равных частей | г) восемь равных частей |
д) пять равных частей | е) десять равных частей |
ж) семь равных частей | з) двенадцать равных частей |
В
ыполнить
чертежи пластин в указанных масштабах.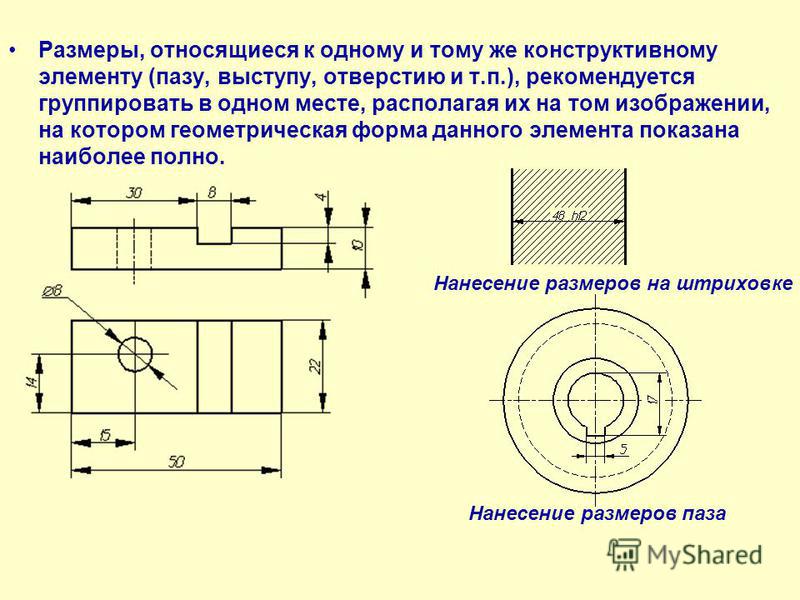
11
ЛИНИИ ЧЕРТЕЖА. ГОСТ 2.303-68 ЕСКД — Студопедия
Поделись
| Наименование | Начертание | Толщина линии по отношению к толщине сплош- ной основной линии | Основное назначение |
| 1. Сплошная толстая основная | S | 1.1.Линии видимого контура, условные изображения элементов конструкций на схемах расположения сборных конструкций. 1.2.Линии перехода видимые. 1.3.Линии контура вынесенногосечения. 1.4.Линии контура сечения, входящего в состав разреза. 1.5.Линии рамки рабочего поля чертежа. 1.6.Линии форм основных надписей и спецификаций. 1.7.Засечки размерных линий, стрелки знаков отметок уровней. | |
| 2. Сплошная тонкая | От S/2 до S/3 | 2.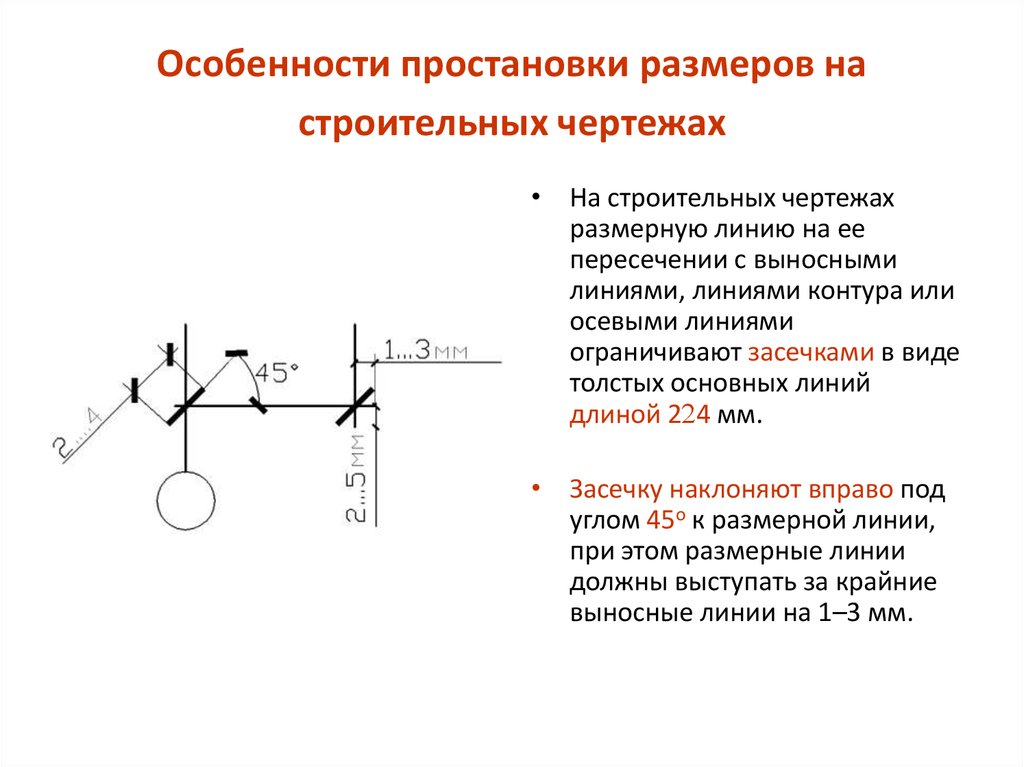 1.Линии контура наложенного сечения.
2.2.Линии размерные и выносные.
2.3.Линии штриховки.
2.4.Линии-выноски.
2.5.Подчеркивание различных надписей.
2.6.Полки линий-выносок.
2.7.Линии для изображения пограничных деталей.
2.8.Линии ограничения выносных элементов на видах, разрезах и сечениях.
2.9.Линии перехода воображаемые.
2.10.Линии упрощённых контурных очертаний строительных конструкций.
2.11.Оси проекций, следы плоскостей, линии построения характерных точек.
2.12.Линии видимых контуров в разрезах на строительных чертежах, распологающихся за плоскостью сечения, линии заполнения проёмов, линии знака открывания оконных переплётов наружу.
2.13.Маркировочные и ссылочные кружки.
2.14.Линии внешней рамки.
2.15.Линии форм основных надписей и спецификаций.
| |
| 3. Сплошная волнистая | От S/2 до S/3 | 3.1.Линии обрыва.
3.2.Линии разграничения вида и разреза.
3.3.Линии замкнутого контура изменённой (или заменённой) части изображения.
| |
| 4. Штриховая | От S/2 до S/3 | 4.1.Линии невидимого контура. 4.2.Линии перехода невидимые. 4.3.Линии знака открывания оконных переплётов внутрь помещения. | |
| 5.Штрихпунктирная | От S/2 до S/3 | 5.1.Линии осевые и центровые. 5.2.Линии сечени, являющиеся осями симметрии для наложенных или вынесенных сечений. | |
| 6.Штрихпунктирная утолщённая | От S/2 до 2/3S | 6.1.Линии, обозначающие поверхности, подлежащие термообработке или покрытию. 6.2.Линии для изображения элементов, расположенных перед секушей плоскостью. | |
| 7. Разомкнутая | От S до 1 1/2S | 7.1.Линии сечений. | |
| 8. Сплошная тонкая с изломами | От S/2 до S/3 | 8. 1.Длинные линии обрыва
| |
| 9.Штрихпунктирная с двуми точками | От S/2 до S/3 | 9.1.Линии сгиба на развёртках. 9.2.Линии для изображениячастей изделий в крайних или промежуточных положениях. 9.3.Линии для изображения развёртки, совмещённой с видом. |
Примечание:
Толщина основной сплошной линии должна быть в пределах 0.5 … 1.4 мм в зависимости от величины и сложности изображения, а также формата чертежа.
Толщина линий одного и того же типа должна быть одинаковой для всех изображений на данном чертеже, вычерчиваемых в одинаковом масштабе.
Задание 1. Вычертить приведённые линии и изображения, соблюдая указаное их расположение. Толшину линий выполнить в соответствии с ГОСТ 2.303-68, размеры не наносить.
Метрики в чертежах — простановка размеров
|
Методы нанесения размеров для метрических чертежей аналогичны методам для
неметрические чертежи, но есть некоторые тонкие различия.
В этом материале изложены современные практики.
Размерные линии и линии проекций
Линии проекции используются для обозначения границ размера. Как правило, они нарисованы на расстоянии до 1 мм от контура объекта.Размерные линии используются для обозначения определенного размера. У них есть один или несколько наконечников стрел, которые обычно имеют длину 3 мм и ширину 1 мм.
Тонкие линии типа B используются как для проекционных линий, так и для размерных линии.
Линейные размеры
Обычно линейные размеры указаны в миллиметрах (миллиметрах).Чтобы не указывать « мм » после каждого размера, метка, такая как все размеры в мм или если не указано иное все размеры в мм ‘ обычно содержится в основной надписи.
Если размер меньше единицы, перед ним следует использовать начальный ноль. десятичная точка.
например. 0,5
После преобразования в микрофильм и последующего повторного увеличения десятичная дробь
точка иногда может стать нечитаемой.
Во избежание возможного неправильного прочтения
вместо десятичной точки часто используется запятая.
например. 0,5 25,7
Угловые размеры
Угловые размеры обычно указываются в десятичных градусах, градусах и минуты или градусы минуты и секунды.например. 27,5° 27°30′ 27°30’16”
Если угол меньше одного градуса, следует использовать начальный нуль.
например. 0,5° 0°30′
Методы определения размеров
Обычно используются два метода определения размеров.-
Размеры указаны горизонтально. - Выровненный
Размеры пишутся параллельно размерной линии. Выровненные размеры всегда должны быть читаемы с нижний или право чертежа.
| Однонаправленный размер | Выравнивание размеров |
Габаритные размеры
Когда несколько размеров составляют общую длину, общий размер могут быть показаны за пределами этих размеров компонента.
При указании общего размера один или несколько некритических компонентов размеры должны быть опущены.
Дополнительные размеры
Когда все размеры компонента должны быть указаны, общий длина по-прежнему может быть указана как вспомогательный размер .Вспомогательные размеры не имеют допусков и указаны в скобках.
Размеры не в масштабе
Размеры, не соответствующие масштабу, подчеркнуты.Неполные размеры
Когда размерную линию нельзя полностью нарисовать в нормальном точка окончания, свободный конец оканчивается двойной стрелкой.РАЗМЕРЫ В AUTOCAD – Evolve Consultancy
Технический чертеж без аннотации неполный. Примечания к чертежу важны для передачи информации о дизайне или уточнения замысла, который невозможно изобразить с помощью одних линий.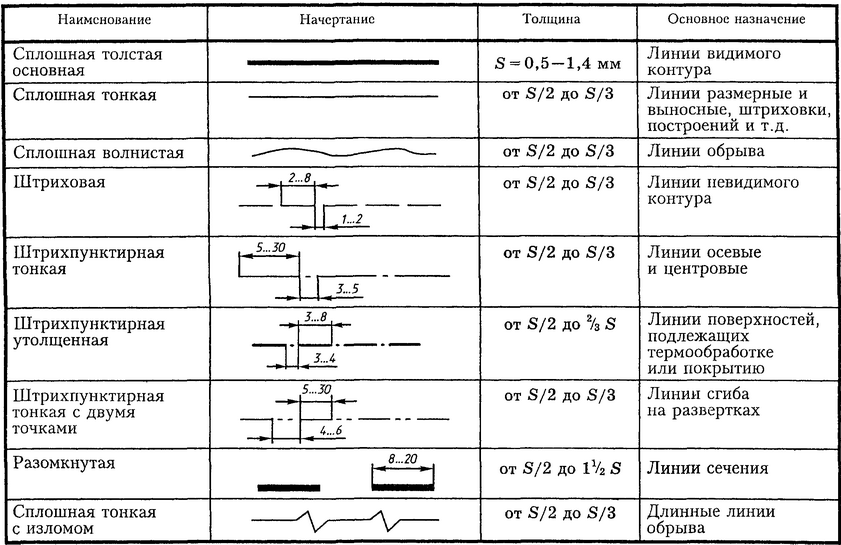
Измерение расстояний по масштабированному напечатанному чертежу является неточным. Размеры позволяют отображать точные значения на чертеже, который затем можно использовать для строительства.
Простановка объектов
Вы можете получить доступ к инструментам простановки размеров на ленте Вкладка «Аннотации » > панель «Размер ». Необходимый инструмент измерения можно выбрать из раскрывающегося списка Dimension .
Линейный
Инструмент измерения Линейный измеряет горизонтальные или вертикальные расстояния. Чтобы создать размеры Linear , щелкните точки 1, а затем 2, чтобы определить элемент, размер которого необходимо измерить. Щелкните точку 3, чтобы найти размерную линию. Размерное расстояние будет показывать вертикальное или горизонтальное расстояние в зависимости от того, перемещаете ли вы курсор в горизонтальном или вертикальном направлении при размещении точки 3.
Командная строка: Чтобы запустить инструмент Linear Dimension из командной строки, введите « DIMLIN » и нажмите [ Enter ].
Выровненный
Инструмент измерения Выровненный измеряет длину вдоль объекта.
Чтобы создать размер Выровненный , щелкните точки 1, а затем 2, чтобы определить элемент, размер которого необходимо измерить. Щелкните точку 3, чтобы найти размерную линию.
Командная строка: Чтобы запустить инструмент Aligned Dimension из командной строки, введите « DIMALI » и нажмите [ Enter ].
Угловой
Инструмент измерения Угловой измеряет угол между двумя объектами.
Чтобы создать размер Angular , выберите объект 1, а затем объект 2, чтобы определить элементы, создающие угол. Щелкните точку 3, чтобы найти размерную линию.
Командная строка: для запуска Угловой размер в командной строке введите « DIMANG » и нажмите [ Enter ].
Длина дуги
Инструмент измерения Длина дуги измеряет длину дуги.
Чтобы создать размер Длина дуги , выберите объект 1, затем щелкните точку 2, чтобы разместить размерную линию.
Командная строка: Чтобы запустить инструмент Измерение длины дуги из командной строки, введите « DIMARC ” и нажмите [ Введите ].
Радиус
Инструмент измерения Радиус измеряет радиус дуги или окружности.
Чтобы создать размер Радиус , выберите объект 1, затем щелкните точку 2, чтобы найти размерную линию.
Командная строка: Чтобы запустить инструмент Radius Dimension из командной строки, введите « DIMRAD » и нажмите [ Enter ].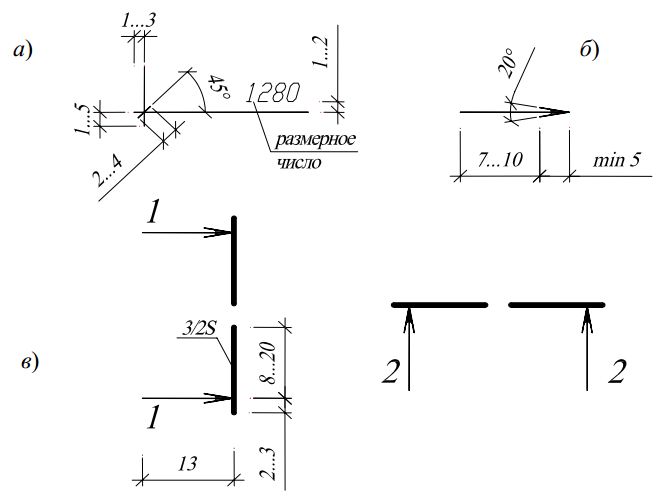
Диаметр
Инструмент измерения диаметра измеряет диаметр дуги или окружности.
Чтобы создать размер Диаметр , щелкните объект 1, затем щелкните точку 2, чтобы найти размерную линию.
Командная строка: Чтобы запустить инструмент Diameter Dimension из командной строки, введите « DIMDIA » и нажмите [ Enter ].
Излом
Инструмент измерения Излом измеряет радиус дуги или окружности, но размещает линию выноски в альтернативном месте (в предполагаемой точке) по отношению к центральной точке дуги или окружности. Изгиб указывает, что размерная линия не указывает на центр окружности. Этот инструмент можно использовать, когда пространство ограничено или радиус дуги большой.
Чтобы создать размер с изломом , щелкните дугу, размер которой необходимо нанести (точка 1). Щелкните точку 2, чтобы определить предполагаемую центральную точку.
Щелкните точку 3, чтобы найти размерную линию и текст. Щелкните точку 4, чтобы найти излом внутри размерной линии.
Командная строка: Чтобы запустить инструмент Jogged Dimension из командной строки, введите « JOG » и нажмите [ Enter ].
Ординат
Ординат 9Размеры 0179 используются для определения значения координаты X или Y точки. Щелкните точку 1, чтобы определить местоположение точки, щелкните точку 2, чтобы найти размерную линию. Ординатные размеры особенно полезны для высот или сеток OS, которые используют определенные координаты.
Примечание: На ординате будет отображаться значение X, если вторая точка находится выше или ниже первой точки. Значение Y будет отображаться, если ваша вторая точка находится сбоку от первой точки.
Командная строка: Чтобы запустить инструмент Ordinate Dimension из командной строки, введите « DIMORD » и нажмите [ Enter ].
Quick Dimension
Инструмент Quick Dimension используется для определения размеров нескольких элементов.
Quick Dimensions можно добавить, щелкнув инструмент Quick Dimension на ленте вкладка Annotate > панель Dimensions .
Командная строка: Чтобы запустить инструмент Quick Dimension из командной строки, введите « QDIM » и нажмите [ Enter ].
Выберите все объекты, которые вы хотите измерить (объекты 1). Вы можете либо выбрать их по 1 за раз, либо использовать выбор пересекающегося окна для выбора нескольких объектов.
Щелкните точку 2, чтобы найти размерную линию.
Продолжить
Инструмент Продолжить используется для добавления дополнительных размеров к линейному, выровненному угловому размеру или размеру длины дуги.
Продолжить работает только с существующим размером Linear или Alignment .
Он берет настройки и высоту из существующего выбранного размера.
Примечание: Направление зависит от выбранной выносной линии. Если вы выберете правую выносную линию, измерение начнется с правой стороны, если вы выберете левую выносную линию, измерение будет производиться с левой стороны.
Вы можете создать размер Продолжить , нажав кнопку Инструмент «Продолжить» на ленте Вкладка «Аннотации» > панель Размеры ..
].
Размер Продолжить создается путем выбора уже созданного размера Линейный или Выровненный (1), а затем щелчком по последующим точкам (2, 3 и 4).
Базовая линия
Базовая линия Размеры измеряют расстояние от начальной точки до нескольких других точек.
Базовая линия работает только с существующим размером Linear или Alignment .
Он берет настройки и высоту из существующего выбранного размера.
Примечание: Направление зависит от выносной линии, которую вы нажимаете. Если вы выберете правую выносную линию, она будет измеряться с правой стороны, если вы выберете левую выносную линию, она будет измеряться с левой стороны.
Вы можете создать размер Базовая линия , щелкнув инструмент Базовая линия на вкладке ленты Аннотации > панель Измерения .
Командная строка: Чтобы запустить инструмент Baseline Dimension из командной строки, введите « DIMBASE » и нажмите [ Enter ].
Размер Базовая линия создается путем выбора уже созданного Линейного или Выровненного размер (1), затем, щелкнув последующие точки (2, 3 и 4).
Мультивыноска
Мультивыноска Инструмент измерения создает стрелки и текст, указывающие на объекты.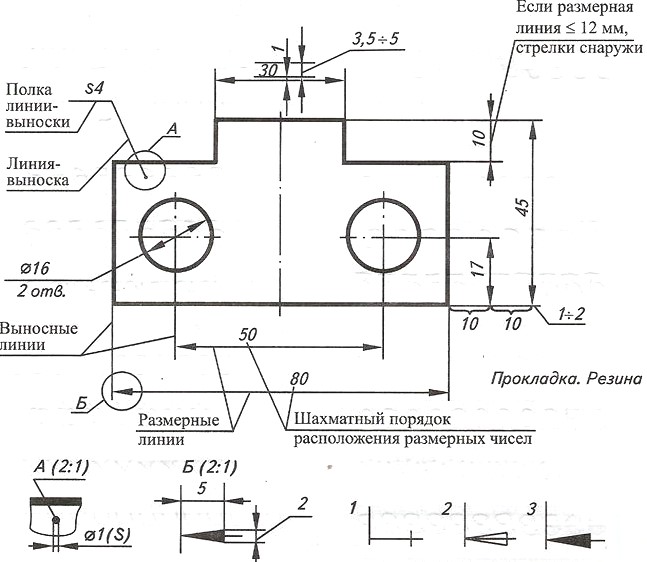
Чтобы создать Мультивыноски , щелкните вкладку ленты Аннотации > панель Выноски > кнопку Мультивыноска .
Командная строка: Чтобы запустить инструмент Multi Leader из командной строки, введите « MLD ” и нажмите [ Введите ].
Щелкните точку 1, чтобы найти начало мультивыноски . Щелкните точку 2, чтобы найти конец мультивыноски . 3 введите текст, который вы хотите отобразить.
Чтобы добавить дополнительные выноски к мультивыноске , нажмите кнопку «Добавить выноску » на ленте вкладка «Аннотировать » > панель «Выноски ».
Щелкните существующий Мультивыноска (1), чтобы определить, к чему вы хотите добавить Выноска . Щелкните точку 2, чтобы определить положение стрелки дополнительной линии Выноска .
Ассоциативные размеры
При размещении размеров по умолчанию создаются Ассоциативные . Ассоциативный размер будет автоматически корректироваться, если геометрия, которую он измеряет, будет изменена.
Ассоциативность размеров управляется из параметров AutoCAD . Чтобы отобразить параметры AutoCAD, щелкните правой кнопкой мыши командную строку и выберите параметры.
Появится диалоговое окно параметров. Функцию ассоциативности размеров можно найти на вкладке Параметры пользователя , установив и сняв флажок Сделать новые размеры ассоциативными .
Если этот параметр отмечен (настройка по умолчанию), размеры будут связаны с объектами. Если объект изменен, размер будет скорректирован в соответствии с ним. Это предпочтительный метод простановки размеров, поскольку он сохраняет правильное значение размера при редактировании геометрии.
Если не отмечен , измерение не связано ни с какими объектами.
Если позже геометрия будет скорректирована, размер останется в исходном месте, и его потребуется изменить вручную.
Стили размеров
Внешний вид отдельных размеров можно изменить с помощью палитры свойств, но использование стилей обеспечит согласованность.
Чтобы просмотреть диалоговое окно «Диспетчер размерных стилей », щелкните размерный стиль 9.0179 на вкладке Лента Annotate > панель Размеры .
Командная строка: Чтобы открыть Dimension Style Manager из командной строки, введите « DDIM » и нажмите [ Enter ].
Доступные стили будут перечислены в разделе Стили диалогового окна Диспетчер размерных стилей .
Подстили будут отображаться связанными с Стиль . Подстили используются там, где требуются различные свойства для определенного инструмента измерения, например.
наконечник стрелки для Выноски отличается от других размеров в родительском стиле.
Создание размерных стилей
Новые размерные стили создаются нажатием кнопки Создать . Появится диалоговое окно Создать новый размерный стиль , позволяющее ввести Имя нового стиля для вашего размерного стиля. Вы должны выбрать существующий размерный стиль в качестве отправной точки.
После создания нового стиля появится диалоговое окно Новый размерный стиль со всеми свойствами начального размерного стиля.
Вкладки в верхней части диалогового окна управляют различными аспектами размеров.
Размер ниже показывает, какая вкладка используется для изменения каждой части измерения.
Линии
Вкладка Линии управляет внешним видом размерных и выносных линий.
На изображении показаны выносные и размерные линии
Цвет управляет цветом размерных линий или выносных линий
Тип линии управляет типом размерных линий.
В разделе «Выносные линии» есть два варианта типа линии: Linetype ext line 1 и Linetype ext line 2, , где 1 является первой размещенной выносной линией.
Вес линии управляет весом линий Размерных линий или Выносных линий.
Базовый интервал — это расстояние между текстом и размерной линией.
Подавить размерную линию / внешнюю линию позволяет удалить размерные или выносные линии, чтобы они не отображались. Это может быть полезно при размещении размерных или выносных линий поверх другой геометрии, например линий сетки, чтобы размер не закрывал размерную линию.
Выход за пределы затемненных линий — расстояние, на которое выносные линии проходят над размерными линиями и за ними.
Смещение от начала координат — это расстояние от измеряемого объекта до начала выносных линий.
Выносные линии фиксированной длины — это длина размерных линий, которую можно зафиксировать, чтобы размеры выглядели аккуратно.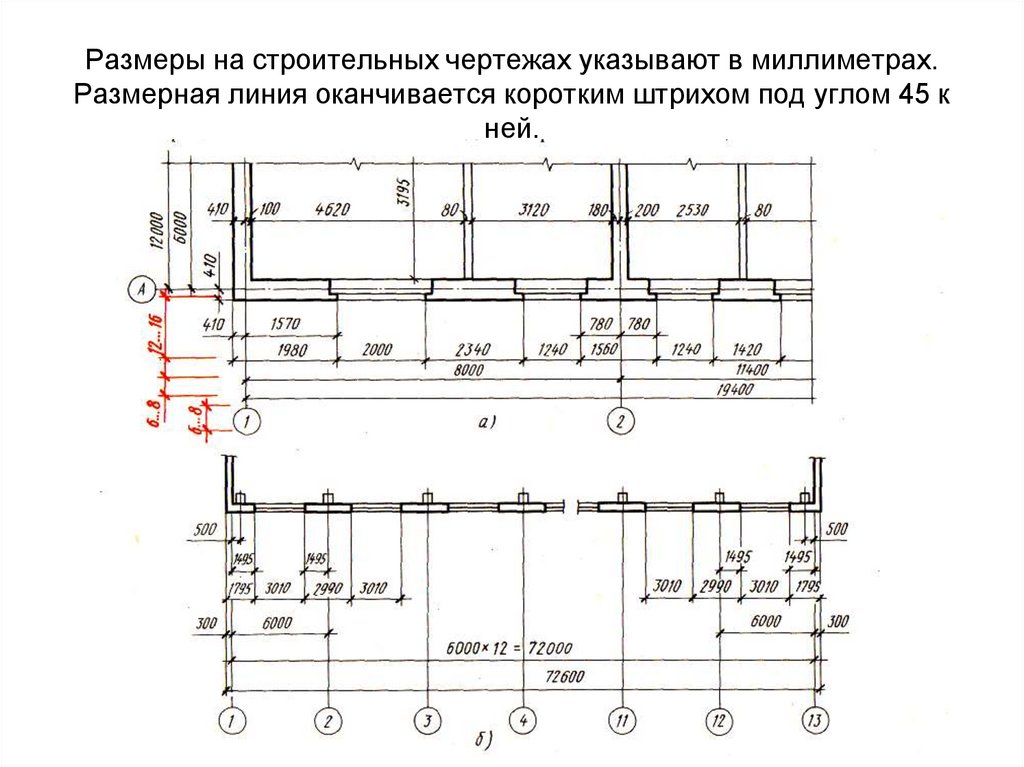
Чтобы изменить длину размерной линии, на вкладке Линии отметьте параметр Выносные линии фиксированной длины и введите длину размерных линий в поле .0178 Длина коробка. Каждый новый размер теперь будет иметь выносные линии, фиксированные по длине, указанной в поле Длина .
Символы и стрелки
Вкладка «Символы и стрелки» управляет наконечниками стрелок в конце размерных линий и маркерами центра.
Наконечники управляет типом и размером наконечников стрелок на концах размерных линий.
Метки центра управляет внешним видом при маркировке центральных точек окружностей и дуг. Довольно часто важно использовать метки центра для разметки криволинейного элемента.
Разрыв размера — это размер метки разрыва при использовании размеров с изломом.
Символ длины дуги управляет расположением символа размера длины дуги.
В примере показано обозначение Исходный размерный текст .
Размер излома радиуса управляет углом излома для размеров Изгиб .
Размер линейного выступа управляет коэффициентом высоты излома как отношением размера текста для размеров излома.
Текст
Вкладка “Текст” управляет внешним видом текста. Его не следует путать с вкладками «Основные» и «Вторичные единицы», которые управляют значением текста.
Внешний вид текста управляет стилем используемого текста, цветом и высотой. (Дополнительную информацию о тексте и стилях текста см. в модуле 06-Текст)
Размещение текста определяет положение текста относительно размерной линии.
Вертикальное
Примечание: Размещение JIS (японский отраслевой стандарт) не показано, но совпадает с вариантом Над .
Горизонтальное
Направление просмотра Управляет чтением текста слева направо или справа налево.
Выравнивание текста управляет поворотом текста: поворачивается ли он в соответствии с ориентацией вида, выравнивается ли он с создаваемым размером или соответствует ли он стандарту ISO (который поддерживает весь текст горизонтально).
Подгонка
Параметры подгонки определяют реакцию текста в размере на ограниченное пространство и общий масштаб текста.
Параметры вписывания управляет перемещением текста и стрелок вокруг выносной линии, если места недостаточно. При определении размеров объектов меньшего размера AutoCAD перемещает текст, стрелки или и то, и другое в зависимости от выбранного параметра.
Размещение текста управляет расположением текста при изменении его положения с помощью параметров «Подгонка».
Масштаб для объектов-размеров управляет масштабом размеров одним из двух способов: вручную и аннотативным методом.
Ручной метод
На вкладке Fit диалогового окна Modify Dimension введите масштаб чертежа, например если ваш рисунок будет масштабироваться 1:100, введите значение « 100 » в поле Использовать общий масштаб . Это приведет к масштабированию атрибутов размера, таких как текст и стрелки, на 100.
Annotative Method
На вкладке Fit диалогового окна Modify Dimension установите флажок Annotative , чтобы использовать масштаб файла Annotative Scale для масштабирования размеров.
Масштаб аннотаций
Аннотативные размерные стили основаны на Масштабе аннотаций . Выберите требуемый масштаб аннотаций в Настройки чертежа в нижней части окна приложения.
Если кнопка Добавить масштабы активна, аннотативные объекты будут изменять размер при изменении раскрывающегося значения Масштаб аннотаций.
Выбранный масштаб аннотации будет назначен аннотации.
При активации Annotation Visibility размер аннотации будет изменен для отображения в текущем масштабе аннотации, если этот масштаб назначен объекту. Если выбранный Масштаб аннотации не был назначен, аннотация останется в своем текущем размере. Например, если аннотативному размеру назначен только масштаб 1:50, а Масштаб аннотации изменен на 1:100, размер останется равным 1:50.
При выборе аннотативного объекта отображаются различные масштабы, используемые аннотативным объектом. На диаграмме ниже выбран аннотативный размер. Его текст отображается в масштабах 1:20 и 1:100 .
Первичные единицы
Это единицы, используемые измерениями.
Линейные размеры — это формат единиц измерения расстояния. Вы можете применять префиксы и суффиксы для обозначения используемого формата единиц измерения.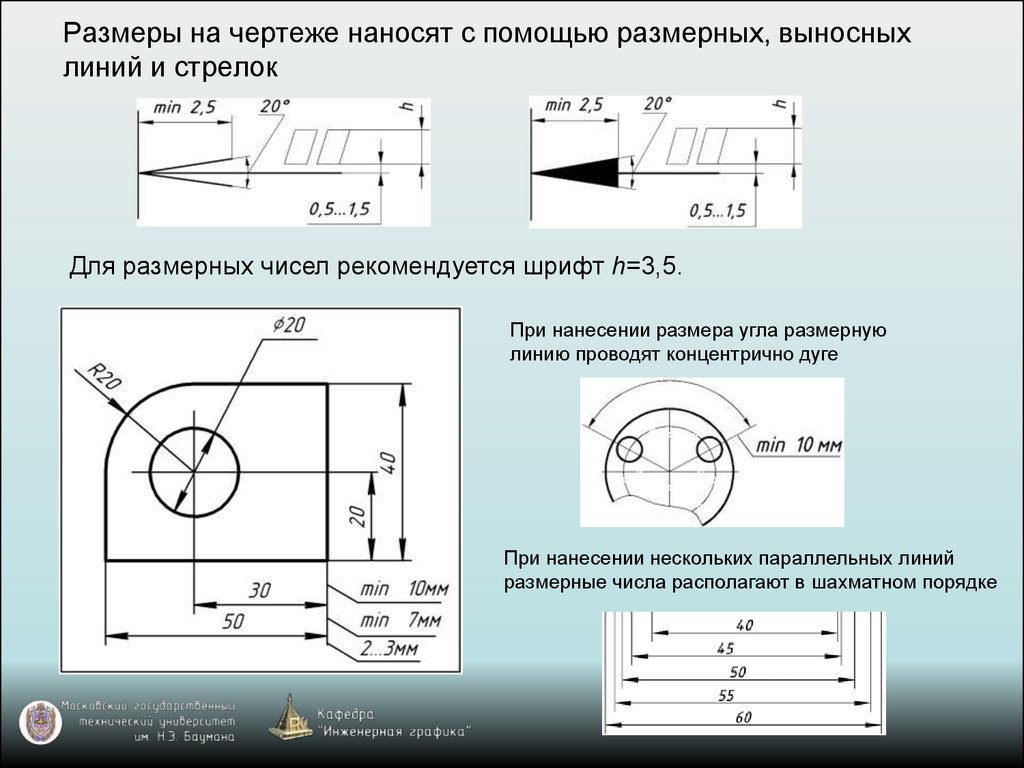
Например, если вы указываете размеры в миллиметрах, введите число 9.0178 Суффикс « мм ».
Масштаб измерения — это масштаб, на который будет умножаться размерная длина, чтобы получить окончательное значение размера. При определении размеров объекта, нарисованного в метрах в миллиметрах, ввод Масштабного коэффициента , равного «1000», даст правильный результат. т. е. если объект имеет длину 5 м, использование размерного стиля с масштабным коэффициентом 1000 приведет к значению размера «5000» (5 x 1000).
Подавление нулей удаляет начальные и конечные нули. Если измеренное значение равно 100,00, отметьте 9Параметр 0178 Trailing даст размерность 100.
Угловые размеры управляет форматом единиц измерения углов.
Альтернативные единицы
Вы можете отобразить два разных значения единиц измерения, например метры и футы, установив флажок Отображать альтернативные единицы на вкладке Альтернативные единицы .
Установите масштабный коэффициент из исходных единиц. Например. Если вы нарисовали в миллиметрах и хотите преобразовать в дюймы, введите масштабный коэффициент «9».0178 0,03937 ”(это 1/25,4, масштабный коэффициент для преобразования мм в дюймы) в поле Multiplier for alt unit .
Примечание: При использовании альтернативных единиц измерения рекомендуется добавлять суффикс (например, дюймов, мм), чтобы уточнить, какие единицы измерения используются.
Раздел Placement управляет расположением альтернативного блока по сравнению с исходными блоками.
Подвижный размерный текст
Чтобы переместить размерный текст, выберите размер, который нужно изменить, чтобы отобразить размеры Захваты . Щелкните в центре Захватите над текстом. Переместите текст в нужное место.
Размерная линия также будет перемещаться для сохранения выравнивания между текстом и размерной линией.