Ось симметрии на чертеже: Симметричные детали на чертеже размеры и линии

Что такое осевая и центральная симметрия?

​ ​

Поможем понять и полюбить математику

Начать учиться

206.3K

Осевая и центральная симметрия — тема для перфекционистов, любителей снимков в отражении и противников заваленного горизонта. Симметрично — значит красиво? Тогда давайте разберемся, что такое симметрия с точки зрения математики.

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

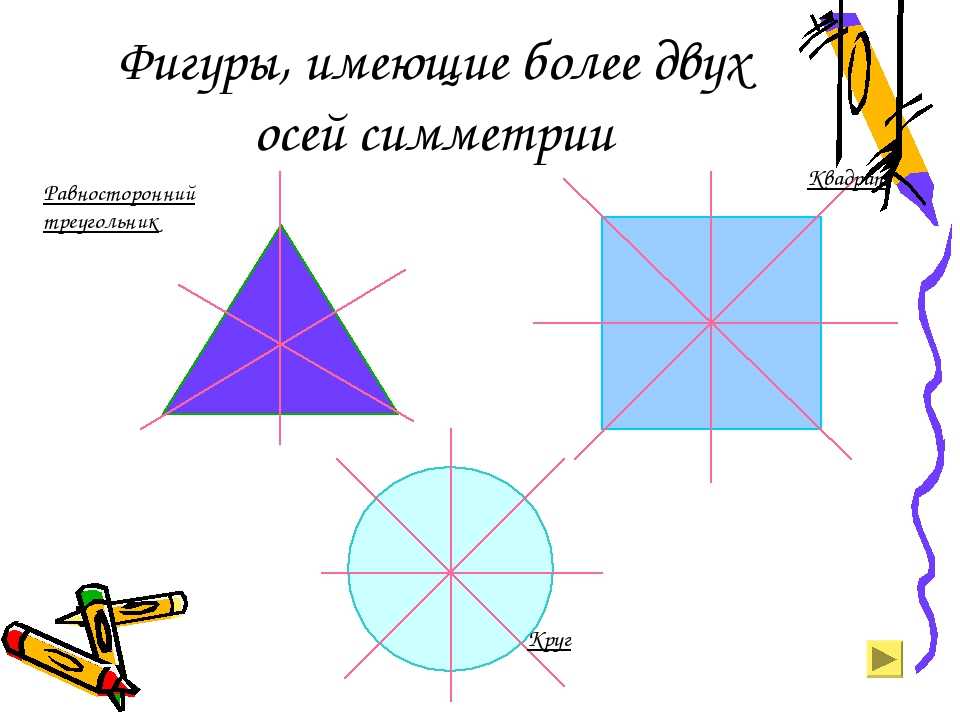
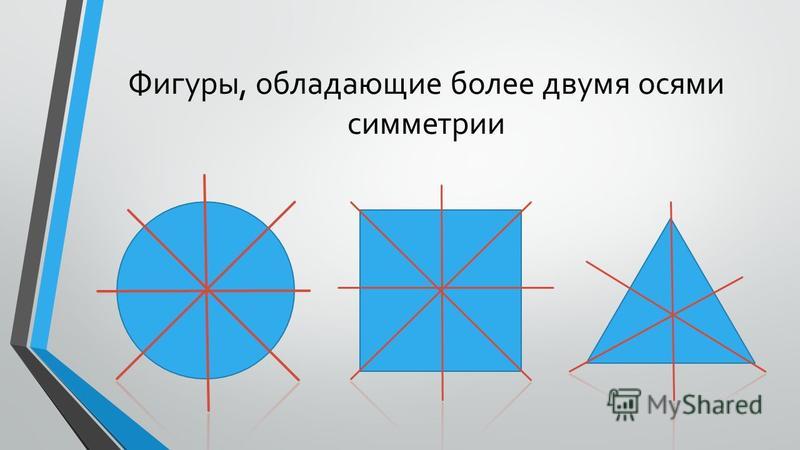
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

 

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

На рисунках осевая симметрия: точки A и B симметричны относительно прямой a; точки R и F симметричны относительно прямой AB

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.


2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.


3. С другой стороны прямой отложим такие же расстояния.


4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.


5. Получаем два треугольника, симметричных относительно оси симметрии.

 

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.


2. Измеряем расстояние от вершин до точек на прямой.


3. Откладываем такие же расстояния на другой стороне оси симметрии.


4. Соединяем точки и строим треугольник A₁B₁C₁.

 

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.


2. Проводим через точку В прямую, перпендикулярную прямой l.


3. Измеряем расстояния от точек А и В до прямой l.


4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.


5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

На картинках центральная симметрия: точка O здесь — центр симметрии

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).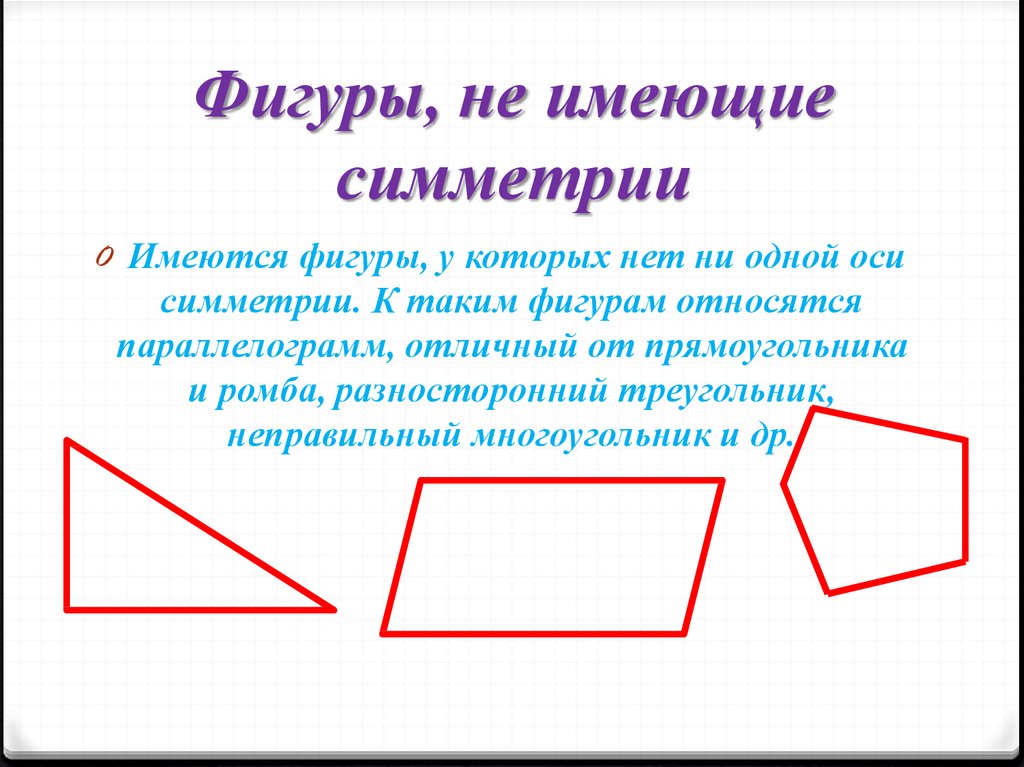

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.


2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).


3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.


4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.


2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.


3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.


4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.


5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

 

Шпаргалки по математике родителей

Все формулы по математике под рукой

Анастасия Белова

К предыдущей статье

193.7K

Прямоугольный параллелепипед. Что это такое?

К следующей статье

111.9K

Как сокращать алгебраические дроби?

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Симметрия объектов

1. Нажмите кнопку Построить скругление .

2.Раскройте список стандартных радиусов поля Радиус скругления и выберите из него значение 10.

3.Последовательно укажите курсором на дугу и отрезок, между которыми нужно построить скругление (рис. 3.82, мишени 1 и 2).

4.Постойте аналогичное скругление в правой части детали.

Рис. 3.82

Задание. Самостоятельно постройте остальные скругления. Примеры выбора объектов показаны на рис. 3.82.

Совет. Перед построением скруглений радиусом 4.5 мм вручную введите данное значение в поле Радиус скругления в Строке параметров,

так как оно отсутствует в списке стандартных радиусов.

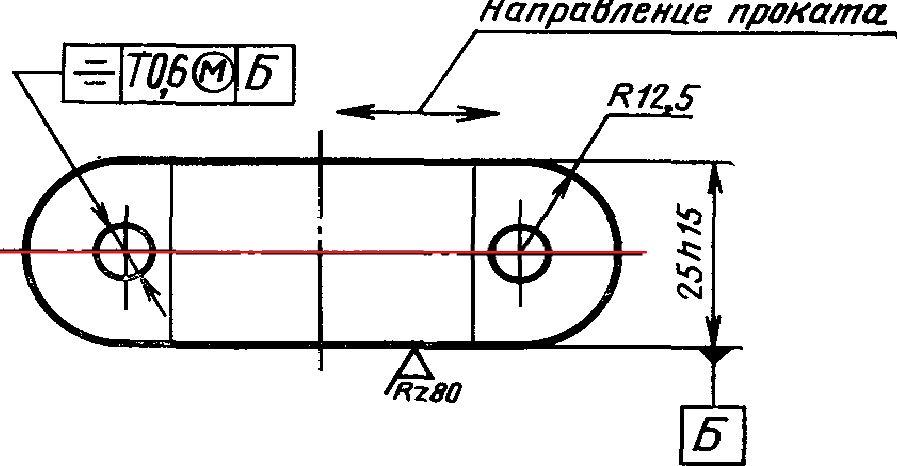
В машиностроительном черчении довольно часто деталь (или отдельные ее элементы) имеет симметричные участки относительно вертикальной, горизонтальной или наклонной оси симметрии. В подобных случаях конструктор должен тщательно начертить один элемент, а симметричные участки строятся с помощью команды Симметрия. Эту команду можно успешно использовать и при отсутствии оси симметрии на чертеже в явном виде. В таком случае ее можно легко построить с помощью вспомогательных построений.

Команда Симметрия на странице Редактирование Инструментальной панели (рис. 3.83, слева) позволяет симметрично отобразить выделенные объекты активного документа относительно произвольной оси симметрии. Если ни один элемент не выделен, команда будет недоступна.

Рис. 3.83

Чтобы использовать в качестве оси симметрии начерченный ранее отрезок

или прямую, нажмите кнопку Выбор объекта на Панели специального управления, а затем укажите курсором нужный элемент.

Кроме того, можно явно задать параметры оси симметрии (координаты точек и угол ее наклона) в полях Строки параметров объектов (рис. 3.83, справа).

После выполнения операции можно задать удаление или сохранение исходных выделенных объектов. Для этого используйте кнопку Исходные объекты в Строке параметров объектов.

Упражнение № 3-22. Полная симметрия

Рис. 3.84

Задание. Закончите чертеж детали, построив ее нижнюю половину.

Приведенная в упражнении деталь представляет собой тело вращения. Такие детали всегда имеют ярко выраженную ось симметрии, поэтому при их построении использование команды Симметрия особенно эффективно.

1. С помощью команды Выделить – Секущей рамкой выделите верхнюю половину детали, за исключением осевой линии. Ее не нужно включать в группу выбора, так как в противном случае после выполнения симметричного ото-

бражения произойдет наложение линий друг на друга. Пример формирования рамки выбора показан на Образце.

2.Вызовите на экран страницу Редактирование Инструментальной панели и нажмите кнопку Симметрия .

3.Поскольку ось симметрии присутствует на чертеже в явном виде, нажмите кнопку Выбор объекта на Панели специального управления.

4.Укажите мишенью на горизонтальную ось симметрии детали в любой ее точке – система выполнила построение симметричного изображения.

5.Щелчком на кнопке Прервать команду прекратите работу команды.

6.Щелчком в любом свободном месте чертежа снимите выделение с исходных объектов.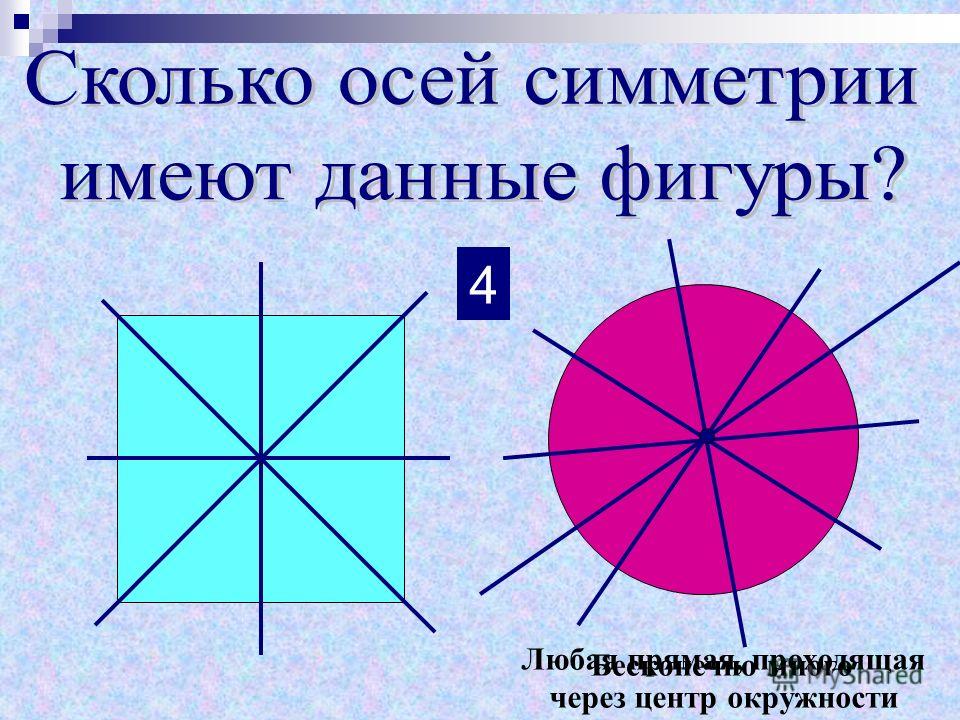

Упражнение № 3-23. Частичная симметрия

Рис. 3.85

Задание. Закончите построение главного вида редуктора, построив его правую половину.

Использование команды Симметрия требует творческого отношения со стороны конструктора. Даже в полностью симметричных конструкциях могут присутствовать элементы, которые удобнее вычерчивать целиком. Например, в данном случае, несмотря на полную симметрию изделия, не следует изображать половинки крышек подшипников в виде отдельных дуг. Такие элементы гораздо удобнее изображать целиком, так построение окружностей выполнять проще, чем построение дуг.

1. С помощью команды Выделить – Рамкой выделите всю половину редуктора целиком, как это показано в Задании.

2.Чтобы избежать наложения объектов, исключите из группы выбора окружности и оси симметрии. Для этого раскройте меню Выделить, затем дополнительное меню Исключить и выполните из него команду Секущей ломаной

(рис. 3.86).

Рис. 3.86

3.Постройте секущую ломаную, как показано в Задании. Все объекты, которые пересечет секущая, будут исключены из группы выбора.

4.Нажмите кнопки Симметрия и Выбор объекта .

5.Укажите мишенью на вертикальную ось симметрии детали в любой ее точке

– система выполнила построение симметричного изображения.

6.Прекратите работу команды и снимите выделение с исходных объектов.

Упражнение № 3-24. Неявная симметрия

Рис. 3.87

Задание. Выполните скругление контура детали Скоба радиусами дуг по размерам, указанным на Образце.

Иногда бывает, что деталь имеет некоторые симметричные участки, но ось симметрии для них отсутствует. Эту проблему легко решить: временно построить

ось симметрии с помощью вспомогательных построений, использовать ее при выполнении симметрии, а потом удалить.

В данном примере червячный вал имеет два абсолютно одинаковых участка, выделенных на Образце рамками 1 и 2. Явной оси симметрии между ними нет. В таком случае нужно тщательно начертить один из участков, а противоположный построить с помощью команды Симметрия. Воображаемая ось симметрии проходит вертикально через середину червяка (отрезок р1-р2).

1. Активизируйте команду Вертикальная прямая из Панели расширенных команд вспомогательных построений (рис. 3.88).

Рис. 3.88

Система просит указать точку, через которую пройдет вспомогательная прямая. Определим ее с помощью локальных привязок.

2.Щелчком правой клавиши мыши в любом свободном месте чертежа вызовите на экран контекстное меню и выполните из него команду Привязка – Сере-

дина (рис. 3.89).

Рис. 3.89

3.Укажите мишенью на верхний горизонтальный отрезок червяка в любой его точке (отрезок р1-р2). После срабатывания привязки щелчком мыши зафиксируйте положение прямой (рис. 3.90).

линий симметрии | Идентификация, рисование, создание, примеры

Введение

У нас есть ряд математических фигур, которые так равномерно сбалансированы в различных размерах и формах. Давайте посмотрим на следующие цифры – 

Мы можем заметить, что для каждой цифры половина на одной стороне пунктирной линии точно идентична половине на другой стороне пунктирной линии. Другими словами, мы можем сказать, что две половины являются зеркальным отражением друг друга. В самом деле, если мы поместим зеркало на пунктирную линию, то изображение одной стороны фигуры будет точно таким же, как фигура по другую сторону пунктирной линии, а затем изображение одной стороны. Это означает, что каждая фигура делится на две одинаковые части относительно пунктирной линии. Когда мы сложим эти фигуры по пунктирной линии, одна половина фигур точно поместится над другой половиной. Пунктирная линия известна как линия симметрии. Итак, как определить линию симметрии?

Что такое линия, это симметрия?

Говорят, что данная прямая имеет линию симметрии или симметрична относительно прямой, если эта прямая делит данную фигуру на две одинаковые половины. Линия называется осью симметрии или линией симметрии.

Типы симметрии линий

Существует два типа симметрий линий, в соответствии с которыми мы можем классифицировать симметрии в различных геометрических фигурах. Эти типы – 

1. Горизонтальные линии симметрии
2. Вертикальная линия симметрии

Рассмотрим их подробнее

Горизонтальная линия симметрии

Если линия симметрии такова, что делит геометрическую фигуру на две одинаковые половины по горизонтали, то она известна. как горизонтальная линия симметрии. Другими словами, горизонтальная линия симметрии — это линия, которая проходит поперек изображения, разделяя его на две одинаковые половины. Эту линию также можно назвать спящей прямой, которая делит изображение или фигуру на одинаковые половины.

Вертикальная линия симметрии

Если линия симметрии такова, что делит геометрическую фигуру на две одинаковые половины по вертикали, она называется вертикальной линией симметрии. Другими словами, вертикальная линия симметрии — это линия, которая проходит вниз по изображению и делит его на две одинаковые половины. Это означает, что вертикальная линия симметрии — это прямая стоячая линия, которая делит изображение или фигуру на две одинаковые половины.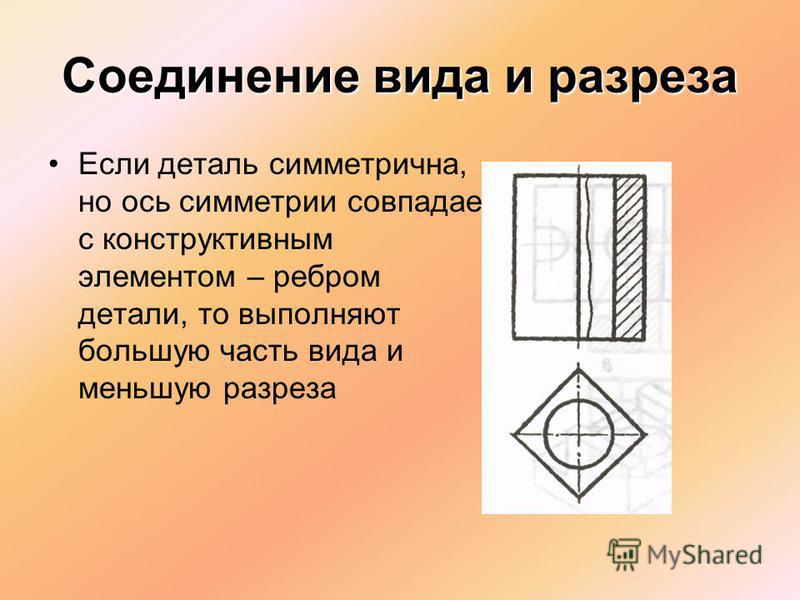

Теперь обсудим количество осей симметрии различных геометрических фигур.

1 Линейная симметрия

Говорят, что геометрическая фигура имеет одну линию симметрии, если она симметрична только относительно одной оси. Рассмотрим несколько примеров.

Симметрия угла

Угол с равными сторонами имеет одну линию симметрии, которая проходит вдоль внутренней биссектрисы угла.

Симметрия равнобедренного треугольника

Равнобедренный треугольник имеет одну линию симметрии, которая проходит по медиане, проходящей через вершину. Это потому, что треугольник называется равнобедренным, только если у него 2 равные стороны. Следовательно, каждый равнобедренный треугольник по определению имеет 1 ось симметрии. Эту линию симметрии можно провести, соединив вершину между равными сторонами и середину противоположной стороны.

Симметрия равнобедренной трапеции

Равнобедренная трапеция имеет две параллельные стороны и две непараллельные стороны одинаковой длины, она имеет только одну линию симметрии вдоль отрезка, соединяющего середины двух параллельных сторон.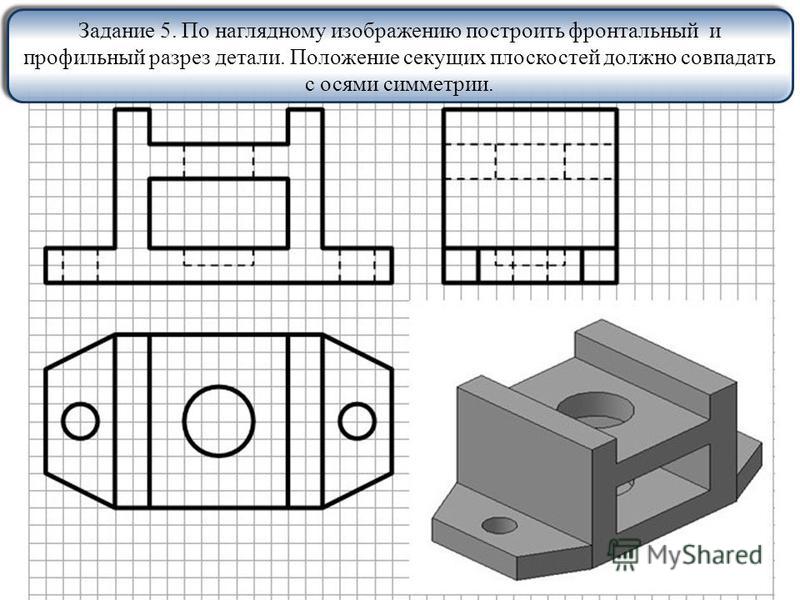 Трапеция – это четырехсторонняя двумерная фигура, две стороны которой параллельны друг другу. Правильная трапеция или также известная как правильная трапеция — это трапеция, у которой одна пара противоположных сторон параллельна, но две другие стороны не обязательно должны быть равны друг другу. Теперь, когда фигура сложена и полностью лежит на самой себе, линия сгиба называется линией симметрии. Равнобедренные трапеции — это те трапеции, у которых одна пара противоположных сторон параллельна, а другая пара противоположных сторон равна. По сути, они такие же, как равнобедренные треугольники.

Симметрия воздушного змея

Воздушный змей имеет одну линию симметрии вместе с одной из его диагоналей. Воздушный змей – это четырехугольник с двумя разными парами смежных сторон, равных по длине

Симметрия наконечника стрелы

Наконечник стрелы имеет одну линию симметрии.

Симметрия полукруга

Полуокружность имеет только одну линию симметрии, перпендикулярную серединному перпендикуляру его диаметра. Это потому, что линия симметрии полукруга является половиной круга, который имеет только одну линию симметрии.

Симметрия по двум линиям

Говорят, что геометрическая фигура имеет две линии симметрии, если она симметрична только относительно двух осевых линий. Рассмотрим несколько примеров.

Симметрия отрезка

У отрезка есть две линии симметрии, а именно сам отрезок и серединный перпендикуляр к отрезку.

Симметрия ромба

Ромб имеет две линии симметрии, проходящие по диагоналям ромба. Это потому, что у ромба четыре равные стороны, но разные углы. Это позволяет ромбу иметь две линии симметрии, одну по горизонтали, а другую по вертикали, что делает его порядка двух, а также угол поворота 180 градусов.

Симметрия прямоугольника

Прямоугольник имеет две линии симметрии вдоль отрезка, соединяющего середины противоположных сторон. Это потому, что прямоугольник представляет собой четырехсторонний многоугольник, две противоположные стороны которого равны и параллельны. Углы прямоугольника всегда равны 90 градусов, а его диагонали всегда равны. Следовательно, линии симметрии в прямоугольнике делят его противоположные стороны на равные части. Важно отметить, что у прямоугольника не может быть диагональной линии симметрии, как у квадрата, потому что стороны не имеют одинаковой длины.

Симметрия по трем линиям

Говорят, что геометрическая фигура имеет три линии симметрии, если она симметрична только относительно трех осевых линий. Рассмотрим несколько примеров.

Симметрия равностороннего треугольника

Равносторонний треугольник имеет три линии симметрии Вдоль трех медиан это потому, что треугольник называется равносторонним треугольником, только если все его три стороны равны, что также означает, что он имеет три равные углы, поэтому он имеет три линии симметрии вдоль трех медиан

Симметрия по четырем линиям

Говорят, что геометрическая фигура имеет четыре линии симметрии, если она симметрична только относительно четырех осевых линий.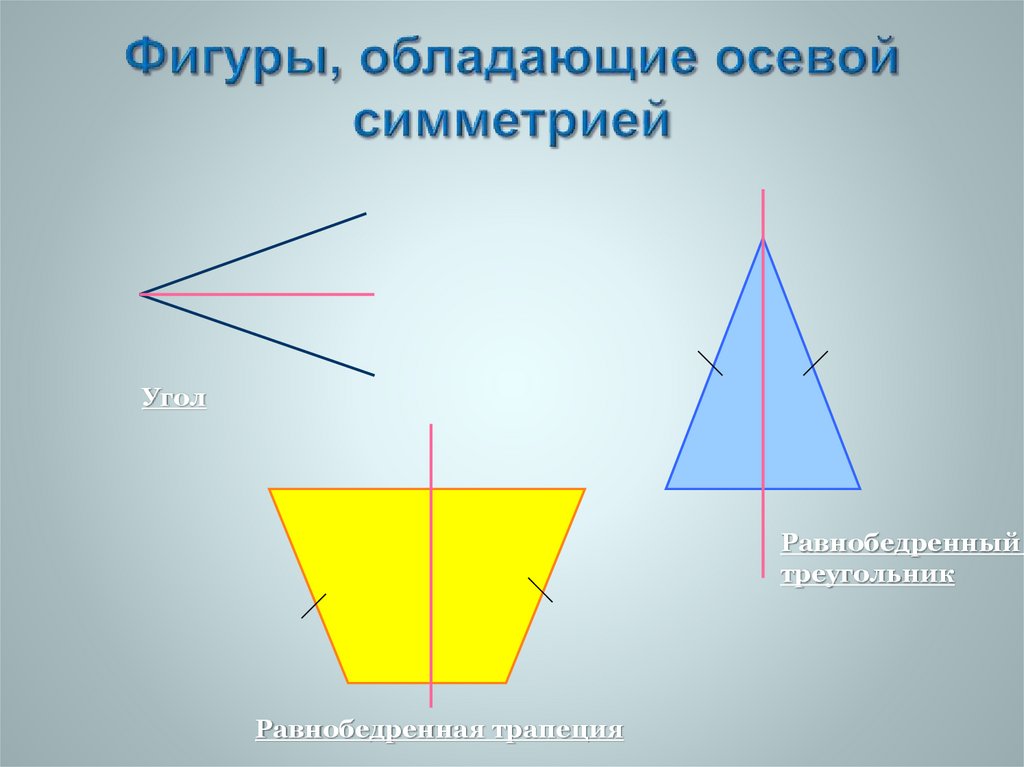 Рассмотрим несколько примеров.

Симметрия квадрата

Квадрат имеет четыре линии симметрии, две длинные отрезки, соединяющие середины противоположных сторон, и две по диагоналям. Другими словами, и диагонали, и линии, соединяющие середины противоположных сторон, то есть биссектрисы, образуют в квадрате симметричные линии.

Симметрия по 5 линиям

Говорят, что геометрическая фигура имеет пять линий симметрии, если она симметрична только относительно пяти осевых линий. Рассмотрим несколько примеров.

Симметрия правильного многоугольника

Правильный пятиугольник имеет пять линий симметрии. Это потому, что правильный пятиугольник имеет пять равных сторон. Итак, он содержит пять линий симметрии.

Симметрия по шести линиям

Говорят, что геометрическая фигура имеет шесть линий симметрии, если она симметрична только относительно шести осевых линий. Рассмотрим несколько примеров.

Симметрия правильного шестиугольника

Правильный шестиугольник имеет шесть линий симметрии. Это потому, что правильный шестиугольник имеет шесть равных сторон. Итак, он содержит шесть линий симметрии. Другими словами, у правильного шестиугольника все шесть сторон равны, а каждый из его углов равен 120°. три симметричные линии проходят вдоль линий, соединяющих середины противоположных сторон, и три проходят по диагоналям.

Бесконечные линии симметрии

Говорят, что геометрическая фигура имеет бесконечные линии симметрии, если она симметрична относительно бесконечных осевых линий. Рассмотрим несколько примеров.

Симметрия прямой

Линия имеет конечную длину и, следовательно, можно считать, что каждая прямая, перпендикулярная данной прямой, делит прямую на равные половины (части). Итак, прямая имеет бесконечное число симметричных прямых, перпендикулярных ей. Итак, прямая имеет бесконечное число симметричных прямых, перпендикулярных ей. Кроме того, линия симметрична самой себе.

Симметрия круга

Круг имеет бесконечное число линий симметрии по всему диаметру. Окружность SA имеет свой диаметр как линию симметрии, а окружность может иметь бесконечное количество диаметров. Следовательно, круг имеет бесконечные линии симметрии.

Примеры симметрии в реальной жизни

Ниже приведен список действий, которые мы можем наблюдать вокруг нашего дома или в нашем районе, которые помогут нам понять симметрию.

1. Симметрия в супермаркете

Вы когда-нибудь наблюдали симметрию в супермаркете? Если мы осмотримся в супермаркете, то увидим, что можем идентифицировать коробки, контейнеры, а также упаковки, которые имеют симметричную форму.

2. Симметрия во фруктах и ​​овощах

Давайте теперь вспомним формы различных фруктов и овощей. Можем ли мы сказать, что некоторые овощи и фрукты, которыми мы пользуемся каждый день, по своей природе асимметричны? О многих яблоках и апельсинах можно говорить о разных линиях симметрии.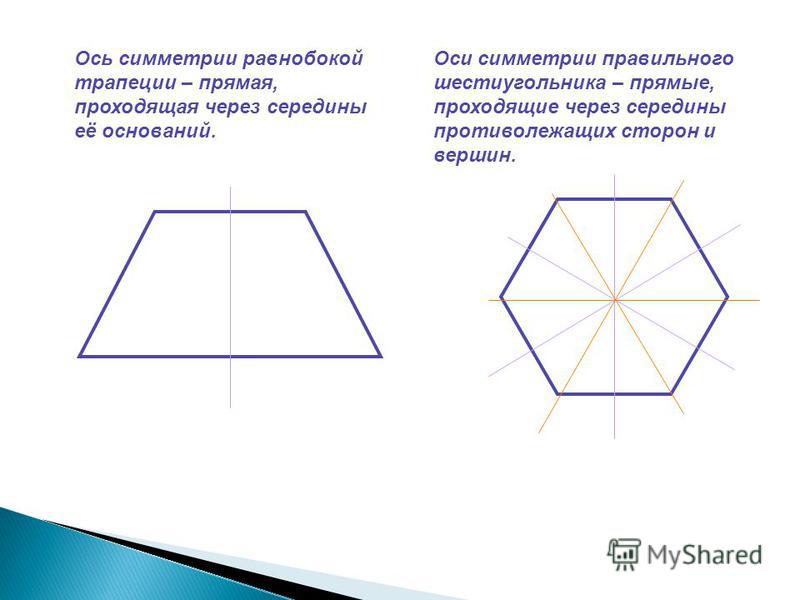

3. Симметрия в природе

Давайте теперь вспомним разные виды цветов, деревьев, листьев для симметрии. Мы можем заметить ряд листьев и цветов, которые имеют симметричную форму.

4. Симметрия в вашей спальне

Посмотрите на линии симметрии на вашей кровати, телевизоре, приставке для видеоигр, компьютере и двери шкафа. Вы заметили, что большая часть мебели в вашем доме или на рабочем месте имеет симметричную форму?

5. Кухня Симметрия

Как и в спальне, мы можем наблюдать симметрию в коробках или контейнерах в кухонных шкафах.

Линия симметрии английских алфавитов

Теперь обсудим линии симметрии некоторых английских алфавитов.

Симметрия заглавного алфавита «А»

Заглавный алфавит «А» имеет одну вертикальную линию симметрии, которая проходит вдоль центральной биссектрисы алфавита.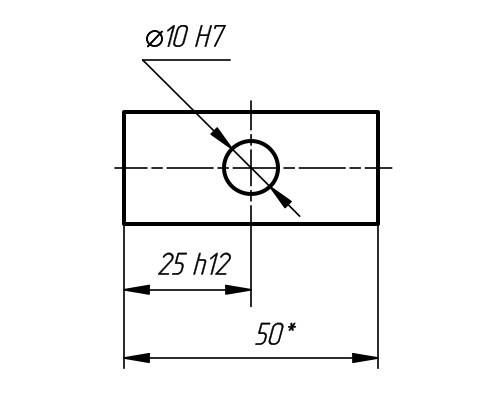

Симметрия заглавного алфавита «B»

Заглавный алфавит «B» имеет одну горизонтальную линию симметрии, которая проходит вдоль центральной биссектрисы алфавита.

Симметрия заглавного алфавита «C»

Заглавный алфавит «C» имеет одну горизонтальную линию симметрии, которая проходит вдоль центральной биссектрисы алфавита.

Симметрия заглавного алфавита «D»

Заглавный алфавит «D» имеет одну горизонтальную линию симметрии, которая проходит вдоль центральной биссектрисы алфавита.

Симметрия заглавного алфавита «E»

Заглавный алфавит «E» имеет одну горизонтальную линию симметрии, которая проходит вдоль центральной биссектрисы алфавита.

Симметрия заглавного алфавита «H»

Заглавный алфавит «H» имеет одну горизонтальную линию симметрии, а также одну вертикальную линию симметрии, которая проходит вдоль центральной биссектрисы алфавита.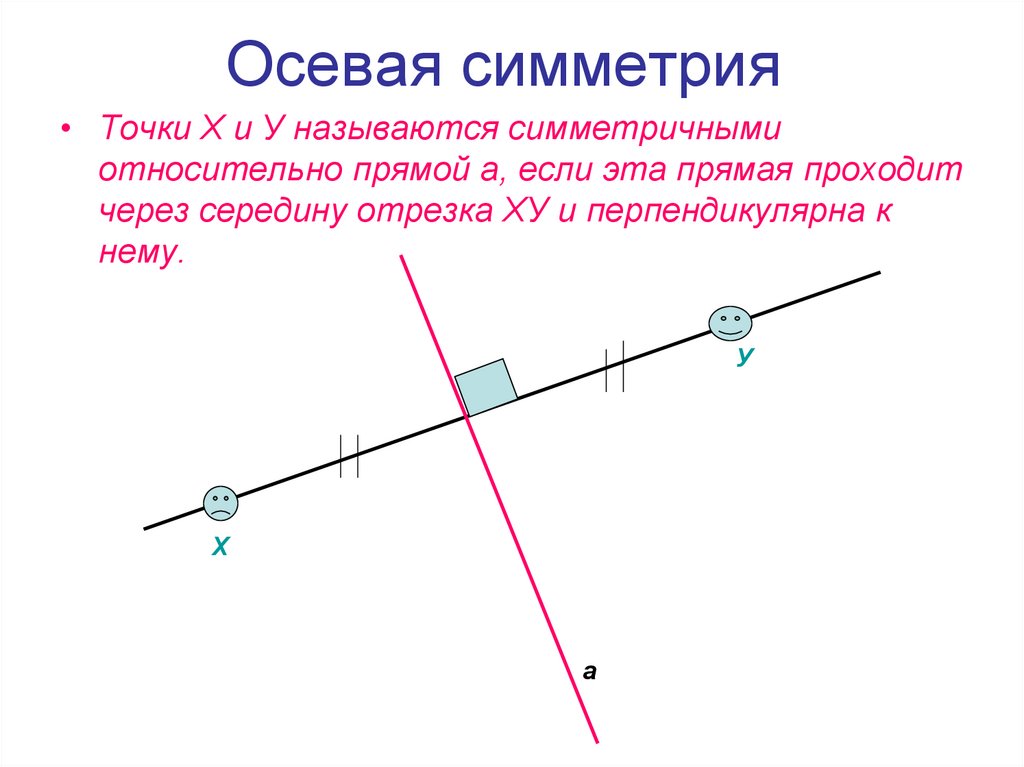

Симметрия заглавной буквы «И»

Заглавный алфавит «I» имеет одну горизонтальную линию симметрии, а также одну вертикальную линию симметрии, которая проходит вдоль центральной биссектрисы алфавита.

Симметрия заглавного алфавита «К»

Заглавный алфавит «К» имеет одну горизонтальную линию симметрии, которая проходит вдоль центральной биссектрисы алфавита.

Точно так же мы можем наблюдать симметрии других алфавитов как – 

Асимметричные формы

Дело не в том, что каждая геометрическая форма симметрична по своей природе. Есть много форм, которые вообще не имеют симметрии. Говорят, что такие фигуры не имеют линии симметрии. Следовательно, говорят, что геометрическая фигура не имеет линии симметрии, если она не симметрична относительно какой-либо оси. Рассмотрим несколько примеров.

Симметрия параллелограмма

Параллелограмм не имеет линии симметрии. Это связано с тем, что форма параллелограмма такова, что его никак нельзя разделить на две одинаковые половины.

Симметрия разностороннего треугольника

Разнонаправленный треугольник без линии симметрии. Это потому, что треугольник называется разносторонним, если ни одна из его двух сторон не равна. Следовательно, через любую вершину разностороннего треугольника не может пройти линия, через которую можно провести медиану, делящую треугольник пополам. Следовательно, разносторонний треугольник не имеет оси симметрии.

Точно так же восьмиугольник симметричен. Если вы сложите его по линии, каждая сторона будет идеально совпадать. Но как узнать, что фигура НЕ симметрична? Посмотрите на пример ниже. Эта фигура не симметрична. Вы можете понять, почему?

Молния несимметрична, потому что она не делится пополам с двумя равными сторонами. Один простой способ проверить, симметрична ли фигура, — нарисовать ее на бумаге и сложить пополам. Если стороны полностью совпадают, он симметричен.

Ключевые факты и резюме

1. Данная линия имеет линию симметрии или симметрична относительно линии, если эта линия делит данную фигуру на две одинаковые половины. Линия называется осью симметрии или линией симметрии.
2. Существует два типа симметрий селезенки, в соответствии с которыми мы можем классифицировать симметрии в различных геометрических фигурах – горизонтальные линии симметрии и вертикальные линии симметрии
3. Если линия симметрии такова, что делит геометрическую фигуру на две одинаковые половины в горизонтальном направлении она известна как горизонтальная линия симметрии.
4. Если линия симметрии такова, что делит геометрическую фигуру на две одинаковые половины по вертикали, она называется вертикальной линией симметрии.
5. Говорят, что геометрическая фигура имеет одну линию симметрии, если она симметрична только относительно одной оси.
6. Говорят, что геометрическая фигура имеет две оси симметрии, если она симметрична только относительно двух осей.
7. Говорят, что геометрическая фигура имеет три оси симметрии, если она симметрична только относительно трех осей.
8. Говорят, что геометрическая фигура имеет три оси симметрии, если она симметрична только относительно трех осей.
9. Говорят, что геометрическая фигура имеет четыре оси симметрии, если она симметрична только относительно четырех осей.
10. Говорят, что геометрическая фигура имеет пять осей симметрии, если она симметрична только относительно пяти осей.
11. Говорят, что геометрическая фигура имеет бесконечные линии симметрии, если она симметрична относительно бесконечных осевых линий. Рассмотрим несколько примеров.
12. Говорят, что геометрическая фигура не имеет линии симметрии, если она не симметрична относительно какой-либо оси.

Дополнительные углы (на тему Праздника фонарей) Рабочие листы по математике
Площадь ромба (на тему Дня смеха) Рабочие листы по математике
Периметр квадрата (на тему Нового года) Рабочие листы по математике

Мы тратим много времени на изучение и составление информация на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

Симметрия – Основы GD&T

GD & T Symbol:

Относительно Datum : Да

MMC или LMC Применимо: NO

Вызовов рисования:

Описание:

9

Описание:

. допуск, который используется для обеспечения того, чтобы два элемента детали были одинаковыми в базовой плоскости. Установленная «истинная» центральная плоскость устанавливается из базы, и для того, чтобы симметрия была в пределах допуска, срединное расстояние между каждой точкой на двух поверхностных элементах должно находиться вблизи этой центральной плоскости. Каждый набор точек на опорных объектах будет иметь среднюю точку, которая находится прямо между ними. Если вы берете все средние точки всей поверхности, они должны находиться в пределах зоны допуска, чтобы быть в спецификации.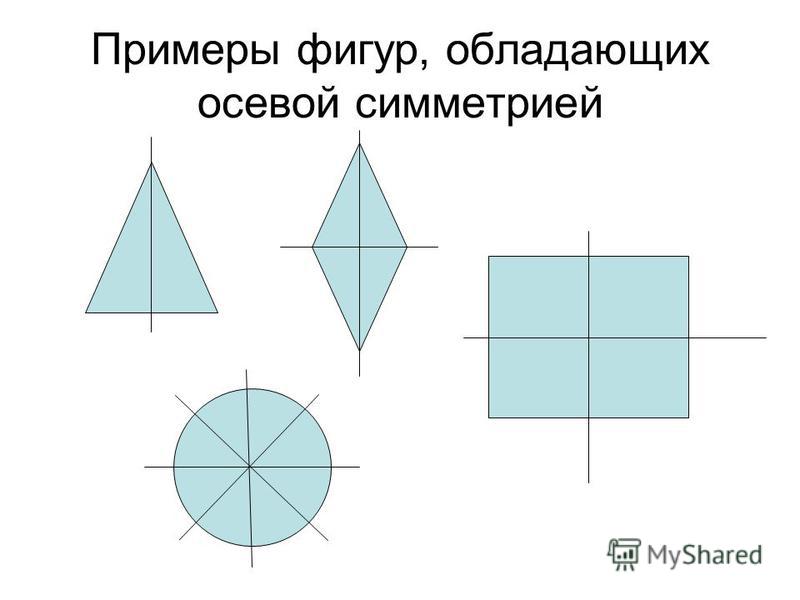 Симметрия не является очень распространенным выноской GD&T, поскольку она имеет очень ограниченное функциональное применение (расположение по центру выполняется с помощью Position), а проверка и измерение симметрии могут быть затруднены (см.: Заключительные примечания).

 

Зона допуска GD&T:

Параллельные плоскости на равных сторонах центральной базовой плоскости. Средние точки симметричных поверхностей должны находиться в пределах этой зоны.

 

Калибровка/измерение:

Как уже говорилось ранее, симметрию очень трудно измерить. Из-за того, что его зона допуска ограничена виртуальной плоскостью, у вас не может быть датчика для правильного быстрого измерения этой функции. Обычно для измерения симметрии КИМ настраивают для расчета теоретической базовой плоскости средней точки, измерения поверхностей обеих требуемых поверхностей, а затем определения того, где лежат средние точки относительно базовой плоскости. Это сложный и иногда неточный метод определения симметричности детали.

Отношение к другим символам GD&T:

Симметрия — это некруглая версия концентричности. В то время как концентричность на самом деле является фокусом симметрии вокруг базовой оси, символ симметрии фокусируется на симметрии относительно базовой плоскости. Оба символа указывают на то, что теоретическая опорная точка центра ограничена определенным пределом, чтобы обеспечить однородность всей конструкции.

Когда используется:

Когда вы хотите убедиться, что центральная плоскость двух симметричных элементов всегда находится точно в центре И имеет ровную форму вдоль поверхности детали. Этот символ используется только для определения баланса массы и распределения формы. Однако в большинстве случаев лучше избегать его использования, так как его очень сложно измерить, и его можно легко заменить допуском положения.

Пример:

Если у вас есть вращающийся U-образный шарнир, канавка которого должна всегда иметь ровный баланс, вам нужно убедиться, что сопрягаемая часть всегда расположена так, чтобы попасть в центр канавки и что форма поверхности должным образом сбалансирована… Вместо того, чтобы расширять канавку, вызывающую ослабление соединения, вы можете ограничить его симметрией.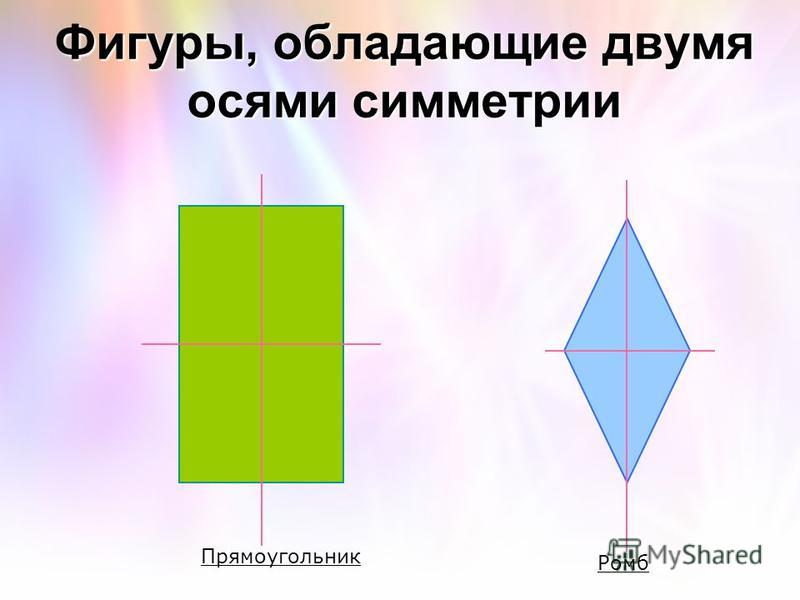

 

Симметрия Пример 1. Вызовите симметрию, чтобы обеспечить центрирование паза на срединной плоскости блока защелки.

Затем необходимо измерить деталь, чтобы убедиться, что все срединные точки сторон защелки симметричны относительно центральной оси. Деталь должна быть измерена следующим образом:

1. Измерьте ширину и расположение обеих сторон эталона блока с помощью базы A (40 мм) и определите, где точно расположена срединная плоскость, чтобы установить нашу зону допуска.
2. Сторона 1 и сторона 2 детали сканируются на наличие их фактических профилей
3. С помощью программы медианы точек сканирования Стороны 1 и Стороны 2 накладываются на плоскости виртуальной зоны допуска и определяются, находятся ли они в пределах допуска.

Заключительные примечания:

В большинстве случаев следует избегать симметрии из-за особых функциональных требований и сложности измерения.