Ось чертеж: Оси на чертеже – обозначение / расположение / названия и какие буквы используются

Оси на чертеже – обозначение / расположение / названия и какие буквы используются

Координационные оси – это линии, которые определяют положение основных несущих конструкций (стен, колонн, пилонов). От их расположения зависит разбивка здания на площадке, которую проводят геодезисты.

Оси на чертеже по ГОСТу

Любой строительный и архитектурный чертеж должен иметь обозначения согласно ГОСТ Р 21.101-2020, который называется «Система проектной документации строительства», часто используется сокращённое наименование СПДС. Каждое здание имеет свои координационные оси, они позволяют понять места расположения несущих конструкций и их привязку. По размеру пролетов между осями можно предположить, какие конструкции используются для перекрытия. Для каждой строительной системы есть свои ограничения и нормы. К примеру, в монолитном каркасе пролеты не превышают 6 метров, а в промышленных зданиях достигают длины в 30 и даже 40 метров.

Обозначение осей на чертежах

Координационные или разбивочные оси обозначаются штрихпунктирной линией, которая проходит через все здание (план, фасад, разрез), деталь или элемент. На одном из концов линии вычерчивается круг, диаметр которого шесть-двенадцать миллиметров, внутри круга арабскими цифрам и прописными буквами указываются наименования осей. Чаще всего вычерчивают круг диаметром 8 миллиметров.

Какие буквы используются в осях чертежей

Практика нумеровать и называть оси существует уже давно, в последнем ГОСТе сохранились прошлые требования к обозначению осей. Для чертежей объектов, возводимых на территории Российской Федерации, используются буквы русского алфавита, из 33 букв не используются только 11, из-за того, что буквенное обозначение может быть неправильно понято, например, буква «З» похожа на цифру «3». К таким неиспользуемым в обозначении осей буквам относится Ё, З, Й, О, Х, Ц, Ч, Щ, Ъ, Ы, Ь. В крупных проектах со сложной системой осей 22 букв может оказаться недостаточно, тогда вводят обозначения с указанием штриха над буквой или используют латинский алфавит (кроме букв I и O) и используют обозначение двумя буквами.

Рисунок 1. На чертеже промаркированы оси, не используются буквы З, Й, Ё,О

Важно, что нумерация ведется последовательно, пропуски и разрывы не допустимы.

Рисунок 2. Буквы на осях чертежей

Ось симметрии на чертеже

Ось симметрии не наносится на строительном чертеже, но она может присутствовать на сборочном чертеже или чертеже детали или виде. Ось симметрии также обозначается штрихпунктирной линией, но у нее на концах нет кружков и маркировки, поэтому ее нельзя перепутать с координационной осью. Толщина штрихпунктирной линии также равна одной трети – половине от толщины основной линии.

Рисунок 3. Ось симметрии на чертеже

Ось вращения на чертеже

При нанесении на чертеж оси вращения также используется правила оформления чертежей. Чтобы правильно читать чертеж, следует помнить, что ось вращения неподвижна, а точки, движущиеся вокруг нее, образуют окружность.

Согласно принятым правилам детали изображают так, как они будут стоять на станке при изготовлении, поэтому чаще всего мы видим их горизонтально.

Оси на строительных чертежах

Прямоугольная система координат позволяет легко ориентироваться в двухмерной плоскости. В строительных чертежах это особенно важно и необходимо. Координатные оси позволяют придерживаться определенных масштабов. На строительном чертеже оси располагают в нижней и левой части чертежа. Нумерация от «1» начинается от левого угла и увеличивается к правому. Принято выносить и располагать оси в один ряд. Расстановка цифр выполняется без пропусков.

Согласно правилам оформления показывают расстояния между соседними осями и общий размер между крайними осями. Буквенные обозначения принято располагать слева от изображения, хотя бывают исключения. К примеру, можно располагать оси справа, если в левой части чертежа недостаточно места. Буквенные обозначения начинаются с буквы «А». Таким образом на пересечении оси «А» и оси «1» располагается самый крайний левый нижний несущий конструктивный элемент.

Рисунок 4. Оси на строительных чертежах

Как оси проходят через конструкции

То, с какой привязкой оси проходят через конструкцию, позволяет понять, как выполняется опирание. К примеру, через толщу стены ось может пройти с привязкой в 120 мм, это будет означать, что плита перекрытия опирается на 120 миллиметров. А у колонны размером 500 на 500 может быть центральная привязка, то есть опирание по 250 мм с каждой стороны.

Также важно помнить, что оси на планах, фасадах и разрезах должны совпадать. На планах оси маркируются и цифрами, и буквами. На разрезах и фасадах видны только оси в одной плоскости в зависимости от направления взгляда.

Рисунок 5. Как оси проходят через конструкции

Чертеж оси с резьбой

На чертежах, где показывается резьбовое соединение, принято показывать ось резьбы. Также как ось симметрии или ось вращения она не имеет на концах дополнительных кружочков и показывается штрихпунктирной линией.

Как выровнять чертеж по оси в Автокад

Одной из самых удобных команд в Автокаде является выравнивание или ALIGN, она позволяет переместить и повернуть объект относительно другого, например, по оси. Сама команда расположена в верхнем меню на вкладке «Редактирование». Для начала нужно выбрать и указать деталь, которая будет выравниваться. Затем нужно выбрать исходную точку на объекте, который перемещается, и целевую, то есть ту, куда будет перенесена исходная точка. Также поступают и со второй точкой. При необходимости программа предложит отмасштабировать и переместить, повернет объект согласно введенным данным.

Рисунок 6. Как выровнять чертеж по оси в Автокад

Расположение осей в круглом здании

Одним из самых сложных примеров является разбивка осей в круглых домах, зданиях и сооружениях, а также в объектах, имеющих криволинейные формы. Чтобы правильно обозначить оси и привязать несущие конструкции, используют маркировку цифрами, они разбивают объект на сектора. Буквами обозначают несущие элементы, которые расположены на окружности.

Рисунок 7. Расстановка осей в круглом здании

Ответы на вопросы

Как обозначаются координационные оси, если объект привязан сразу к нескольким осям?

При изображении повторяющегося элемента, который привязан к нескольким осям, показывают одну штрихпунктирную линию. Если осей менее трех, то номера каждой оси показывают в кружочке друг под другом, если осей больше, то указывают диапазон в формате «33-38».

Рисунок 8. Обозначение осей в секциях

Как ставить оси если здание имеет и круглые, и прямоугольные части?

В этом случае расположение и расстановка должны соответствовать форме. В круглой части расстановка ведется по кругу, а в прямоугольной согласно ортогональной сетке осей. Сложнее всего ставить оси в местах примыкания прямоугольной и криволинейной частей, так как они будут наслаиваться друг на друга. Следует ценить расположение несущих конструкций и отталкиваться от этого.

Рисунок 9. Расстановка осей в криволинейном здании

Какие размерные цепочки поставить в координационных осях?

Через оси проходят две размерные цепочки, на верхней ставятся все размеры между соседними осями с точностью до миллиметра, а на второй указывается размер между крайними осями. Благодаря этим цепочкам становятся понятны габариты объекта.

Рисунок 10. Здание в осях 1-5 и А-Д

Координатные оси здания

Вернуться на страницу «Оформление чертежей»

Обычно маркировочные кружки (их диаметр 6–12 мм) располагают с левой и нижней стороны здания.

Оси наносят согласно ГОСТ Р 21.1101-2013:

5.3 Координационные оси

5.3.1 На изображениях здания или сооружения указывают координационные оси его несущих конструкций, предназначенные для определения взаимного расположения элементов здания или сооружения и привязки здания или сооружения к строительной геодезической сетке или разбивочному базису.

5.3.2 Каждому отдельному зданию или сооружению присваивают самостоятельную систему обозначений координационных осей.

Координационные оси наносят на изображения здания, сооружения тонкими штрихпунктирными линиями с длинными штрихами, обозначают в кружках диаметром 6-12 мм арабскими цифрами и прописными буквами русского алфавита (за исключением букв: Ё, З, Й, О, X, Ц, Ч, Щ, Ъ, Ы, Ь) или, при необходимости, буквами латинского алфавита (за исключением букв I и О).

Пропуски в цифровых и буквенных (кроме указанных) обозначениях координационных осей не допускаются.

Цифрами обозначают координационные оси по стороне здания и сооружения с большим количеством осей. Если для обозначения координационных осей не хватает букв алфавита, последующие оси обозначают двумя буквами.

Пример — АА, ББ, ВВ.

5.3.3 Последовательность обозначений координационных осей принимают по плану, как показано на рисунке 1а: цифровые оси — слева направо, буквенные оси — снизу вверх или как показано на рисунках 1б и 1в.

Рисунок 1

5.3.4 Обозначение координационных осей, как правило, наносят по левой и нижней сторонам плана здания и сооружения.

При несовпадении координационных осей противоположных сторон плана в местах расхождения дополнительно наносят обозначения указанных осей по верхней и/или правой сторонам.

5.3.5 Для отдельных элементов, расположенных между координационными осями основных несущих конструкций, наносят дополнительные оси, которым присваивают обозначение в виде дроби, в числителе которой указывают обозначение предшествующей координационной оси, а в знаменателе — дополнительный порядковый номер в пределах участка между смежными координационными осями в соответствии с рисунком 1г.

Допускается координационным осям фахверковых колонн присваивать цифровые и буквенные обозначения в продолжение обозначений осей основных колонн без дополнительного номера.

5.3.6 На изображении повторяющегося элемента, привязанного к нескольким координационным осям, координационные оси обозначают в соответствии с рисунком:

2а — при их количестве не более 3;

2б — при их количестве более 3;

2в — при всех буквенных и цифровых координационных осях.

Рисунок 2

При необходимости ориентацию координационной оси, к которой привязан элемент, по отношению к соседней оси указывают в соответствии с рисунком 2г.

5.3.7 На планах жилых зданий, скомпонованных из блок-секций, крайним координационным осям блок-секций присваивают обозначения согласно 5.3.1-5.3.3, которые указывают в соответствии с рисунком 3а.

Координационным осям блок-секций, в том числе крайним, присваивают самостоятельные обозначения согласно 5. 3.1-5.3.3 с добавлением индекса «с» (см. рисунок 3б). При необходимости на плане блок-секции указывают обозначения координационных осей здания, скомпонованного из блок-секций.

5.3.8 Трехмерную (3D) электронную модель здания или сооружения выполняют в единой планово-высотной системе координат.

Координатную систему трехмерной модели здания или сооружения изображают тремя взаимно перпендикулярными линиями с началом координат, расположенным в точке пересечения осей 1 и А на нулевой отметке этого здания или сооружения в соответствии с рисунком 4.

Рисунок 4

При этом для прямоугольного в плане здания (см. рисунок 1а) за положительное направление принимают: оси X — в сторону увеличения цифровых обозначений координационных осей, оси Y — в сторону увеличения буквенных обозначений координационных осей, оси Z — вертикально вверх от условной нулевой отметки здания.

Drawabox.com | Часть первая: Основы | Урок 1: Линии, эллипсы и прямоугольники | Эллипсы

Вот куда идет сообщение!

Ненавидите читать? Без проблем. Мы можем прочитать вам текст .

Эта функция доступна совершенно бесплатно . Хотя мы будем следить за тем, насколько возможно покрыть связанные с этим расходы, мы надеемся, что так и останется.

Просто нажмите «Слушайте с помощью Drawabox»!

Что такое эллипс?

Эллипсы чрезвычайно важны и, как известно, раздражают при рисовании. Вы найдете их повсюду в механических чертежах. Автомобили, космические корабли, танки, машины — все, что создано человеком, вероятно, широко использует эллипсы.

Они также занимают видное место в органических рисунках, особенно когда мы смотрим на сечения колбасоподобных форм.

Давайте уделим немного времени изучению того, что они собой представляют, как ведут себя и как их можно использовать.

2D против 3D

Итак, прежде чем мы перейдем к сложным вещам, помните: рисование — это (по крайней мере, в рамках этого курса) о том, чтобы брать трехмерные вещи (например, мир, в котором мы живем) и запечатлевать их на двумерная поверхность , будь то лист бумаги, холст или спина моего друга, который был настолько глуп, что 16-летний мальчик сделал для него татуировку, которая, по сути, навсегда приклеилась к его телу.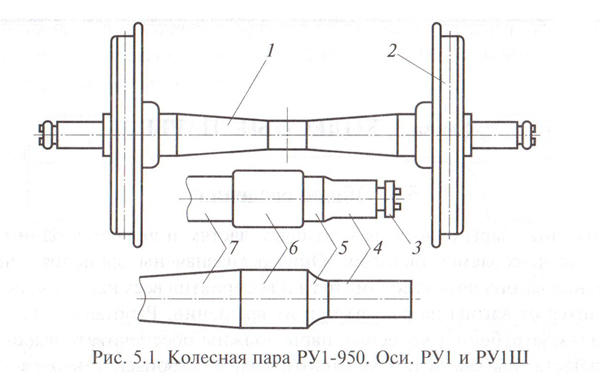

Это означает, что рисование на самом деле связано с выяснением того, как представлять трехмерные объекты, и с пониманием того, как линии и формы, которые мы используем для их захвата, меняются в зависимости от того, как эти трехмерные формы перемещаются и вращаются в пространстве.

На протяжении всего курса я буду обозначать вещи как

в 3D-пространстве или в 2D-пространстве . Обратите внимание на то, что я использую в той или иной ситуации, потому что это имеет значение.

Круги в 3D-пространстве

Для наших целей в этом курсе мы будем использовать эллипсы в 2D-пространстве (нарисованные на странице) для представления окружностей, которые существуют в 3D-пространстве.

В зависимости от того, смотрите ли вы на нее как на двухмерную или трехмерную, эта анимированная диаграмма изображает одну из двух вещей:

• В двухмерном пространстве это ряд эллипсов, от самого широкого до самого узкого.

• В 3D-пространстве это круг, который вращается от лица, обращенного к зрителю, к обращению от него.

Градус

От того, как наш круг (в трехмерном пространстве) повернут относительно зрителя, будет зависеть, насколько широким будет нарисован наш эллипс. Эта ширина (всегда измеряемая по самому узкому

промежутку , проходящему через центр эллипса) называется «градусом», потому что она привязана к углу поворота (в градусах) самого круга относительно зритель.

Когда круг (в 3D-пространстве) обращен к зрителю, он будет самым широким – 90 градусов. Это то же самое, что рисовать круг на странице. По мере того, как трехмерный круг отворачивается от зрителя, эллипс, представляющий его, будет сужаться, пока, наконец, не достигнет степени 0, когда эллипс обращен в сторону.

Градусное смещение

Имейте в виду, что, поскольку это основано на угле между направлением, в котором смотрит круг, и направлением, в котором смотрит зритель, градус фактически изменится, просто перемещая круг в пространстве, не обязательно вращать его.

На этой диаграмме показано, как чем дальше вправо перемещается круг по отношению к зрителю, тем больше становится видна его грань, в результате чего на странице его представляет более широкий эллипс, даже если этот круг не вращается в пространстве.

На протяжении всего курса мы будем называть это понятие «градусным сдвигом» — по сути, это идея о том, что градус нашего эллипса будет сдвигаться вширь или уже в зависимости от того, как он перемещается в пространстве.

Малая ось

Мы называем линию, которая проходит через самый узкий отрезок эллипса и через его центр, его малая ось . Эта линия малой оси разделит эллипс на две равные симметричные половины, поэтому, если его вырезать из страницы и сложить пополам по этой линии, он будет идеально совпадать.

Также есть большая ось , которая проходит перпендикулярно ей (по самому широкому пролету), но на самом деле полезным компонентом является малая ось.

Вектор нормали

Так же, как 2D-эллипс представляет собой 3D-круг, малая ось равна

чрезвычайно полезен для нас из-за того, как эта линия малой оси совпадает и выравнивается с вектором нормали – 3D-линии, которая выходит прямо из поверхности 3D-круга, полностью перпендикулярно этой поверхности.

Это означает, что у нас есть два способа установить ориентацию нашего круга в 3D-пространстве, когда мы рисуем его на нашей 2D-странице:

Если нам нужно, чтобы наш круг был ориентирован определенным образом в более сложной сцене , мы фактически сможем начать с обычной векторной линии, а затем использовать ее в качестве малой оси для нашего эллипса, рисуя эллипс вокруг нее так, чтобы линия разделяла его на две равные симметричные половины по самому узкому промежутку.

Цилиндры

Продолжая, малая ось/вектор нормали также чрезвычайно полезна, когда мы получаем цилиндрические формы. Здесь он служит «позвоночником» нашей формы.

Концы цилиндра имеют один и тот же вектор нормали (в 3D) и малую ось (в 2D). также выравниваются по той же малой оси/вектору нормали.

К счастью для вас, нам не нужно беспокоиться об этом прямо сейчас — они не вступят в игру до Урока 2. Просто полезно увидеть, насколько полезной может быть малая ось эллипса, особенно когда мы пытаемся выяснить все способы, которыми мы можем представить различные свойства круга в трехмерном пространстве.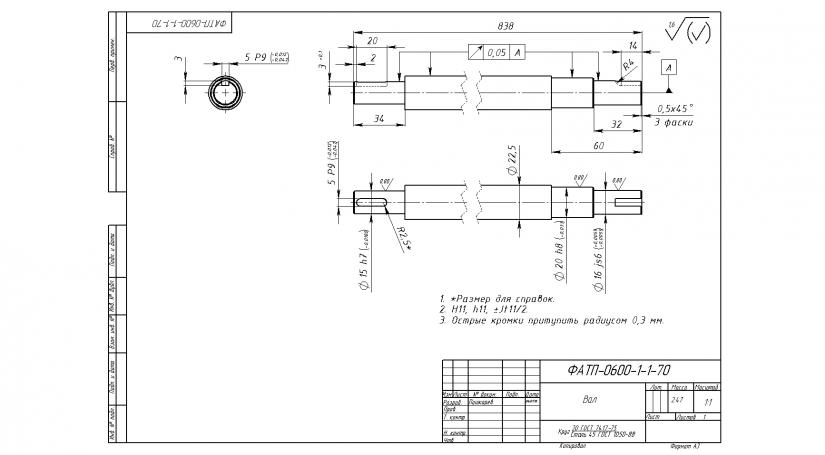

Домашнее задание и упражнения

Домашнее задание по этому разделу следующее:

• 2 заполненные страницы упражнения «Таблицы эллипсов»

• 2 заполненные страницы упражнения «Эллипсы в плоскостях»

• 1 заполненная страница упражнения «Воронки»

Вся работа, назначенная для этого раздела, должна быть выполнена тушью с использованием маркеров/фломастеров, как описано здесь

. В крайнем случае я соглашусь на работу, выполненную шариковой ручкой, но только в крайнем случае. Это исключение только для этого урока, когда ученики начинают.

<<< Строки: Домашнее задание

Ящики >>>

Brigham Young University-Idaho ART 110

Эллипс — это идеальный круг, укороченный в ракурсе. Эллипсы используются для построения цилиндров и конусов.

В следующих разделах рассматриваются части эллипса и способы рисования эллипсов в перспективе.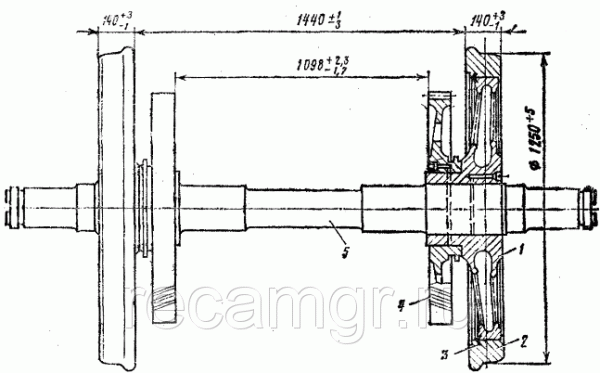



Площади эллипса: В эллипсе площадь половины A всегда будет равна площади половины B.


Площади эллипса: Даже когда эллипс меняет размер, половина А всегда будет иметь ту же площадь, что и половина В.


Обзор эллипса: Большая ось проходит от двух самых длинных частей эллипса. Малая ось проходит от двух самых коротких частей эллипса. Центральная линия эллипса всегда будет иметь то же направление и положение, что и малая ось, и выходит за пределы эллипса.

Чтобы нарисовать эллипс:

1. Определите размер, слегка нарисовав большую ось.

2. Найдите точный центр линии большой оси и нарисуйте другую линию, перпендикулярную главной оси, с расстоянием выше большой оси, равным расстоянию под осью. Это ваша малая ось, и она будет определять шаг эллипса.

3. Аккуратно нарисуйте изогнутые концы на главной оси. Когда обе кривые станут симметричными, слегка нарисуйте оставшуюся часть эллипса выше и ниже большой оси, убедившись, что кривые касаются верхней и нижней части линии малой оси.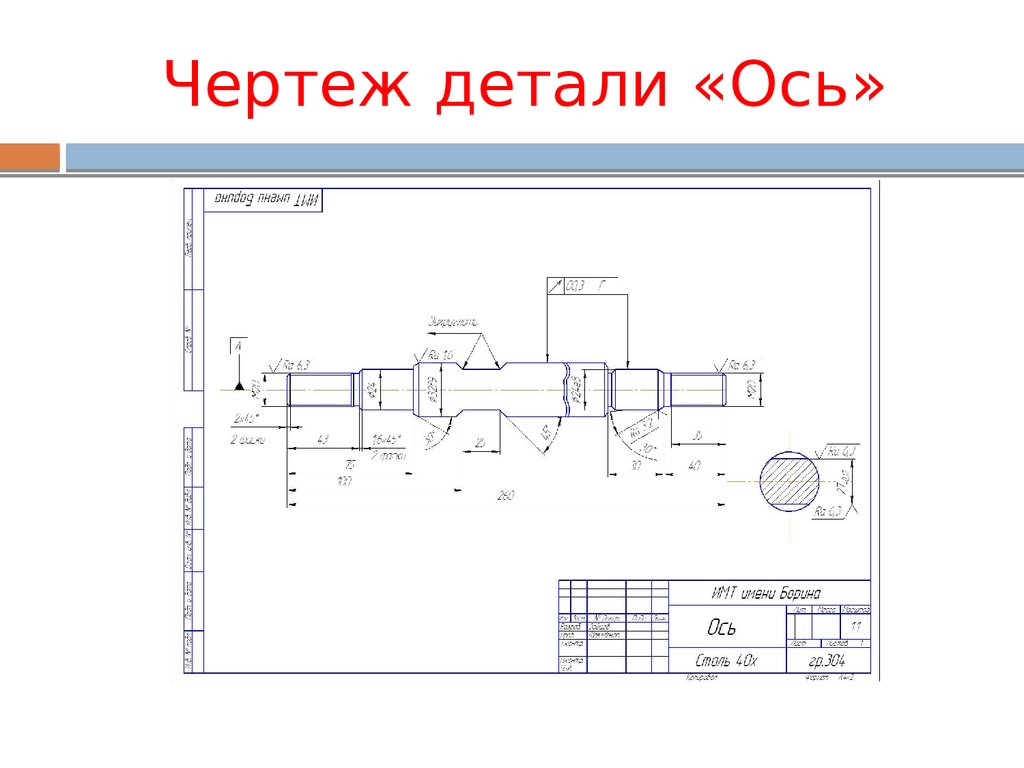 Разделение осевых линий создаст четыре равнозеркальных квадранта.

4. Проверьте и исправьте симметрию и нарисуйте законченные более темные линии.

Эллипсы, содержащиеся в квадратах

Центр эллипса: В этом примере, начиная с квадрата, точный центр был определен путем проведения диагональных линий из угла в угол. Продление вертикальных и горизонтальных линий от центра к внешним краям создало четыре равных квадранта. Круг, помещенный внутри квадрата, будет касаться концов вертикальной и горизонтальной линий.
Центр круга в ракурсе: Когда квадрат/круг уменьшен в ракурсе, верхняя половина круга меньше нижней из-за уменьшения. Вертикальная линия остается малой осью, но горизонтальная линия, указывающая перспективный центр квадрата, не является большой осью. Красная линия представляет собой большую ось и измеряемый центр между верхней и нижней кривыми эллипса. Нажмите на миниатюры ниже, чтобы сравнить верхнюю и нижнюю половины эллипса с правильным расположением главной оси.




Центр перспективы относительно большой оси: Обратите внимание, что красная линия большой оси не проходит через центр перспективы круга в ракурсе и не касается края квадрата в ракурсе. Большая ось всегда будет в самой широкой точке эллипса, причем верхняя половина равна нижней половине.




Внутри эллипса верхняя и нижняя половины всегда идентичны. Большая ось — это самая широкая точка эллипса. Он будет расположен точно в центре малой оси.




Эллипсы на надувном мяче: Обратите внимание, что несмотря на то, что у надувного мяча шесть сегментов разного цвета, они состоят всего из трех эллипсов. Каждый эллипс имеет свою большую и малую оси.
Примечание. Линия на этом надувном мяче соединяет повернутые верх и низ мяча.