Произвольный тупой угол. Прямой, тупой, острый и развернутый угол. Смотреть что такое “Острый угол” в других словарях
В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Навигация по странице.
Определение угла.
Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.
Дадим сначала определение луча.
Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a . Пусть O – некоторая точка прямой a . Точка O разделяет прямую a на две части. Каждая из этих частей вместе с точкой О называется
Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p или луч k ), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА или луч СD ). Покажем изображение и обозначение лучей на чертеже.
Теперь мы можем дать первое определение угла.
Определение.
Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла
.
Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым .
Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.
Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k
, а другая h
), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA
, а вторая сторона угла OB
), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ). Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ).
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая – внешней.
Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.
Определение внутренней области угла приводит нас ко второму определению угла.
Определение.
Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.
Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Дадим еще определения смежных и вертикальных углов.
Определение.
Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.
Из определения следует, что смежные углы дополняют друг друга до развернутого угла.
Определение.
Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.
На рисунке изображены вертикальные углы.
Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.
Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными .
Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол).
Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение углов.
Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.
Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градус .
Определение.
Один градус – это угол, равный одной сто восьмидесятой части развернутого угла.
Градус обозначают символом «», следовательно, один градус обозначается как .
Таким образом, в развернутом угле мы можем уложить 180 углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180 равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть развернутого угла) и ровно 90 раз (половина развернутого угла).
Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения).
Определение.
Минута – это одна шестидесятая часть градуса.
Определение.
Секунда – это одна шестидесятая часть минуты.
Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600 секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .
Определение.
Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.
Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.
Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110 ), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов. На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол.
Из этого утверждения следует, что . Действительно, если углы АОВ и СОD – вертикальные, то углы АОВ и ВОС – смежные и углы СОD и ВОС также смежные, поэтому, справедливы равенства и , откуда следует равенство .
Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана.
Определение.
Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA (как и радиуса OB ) равна длине дуги AB , поэтому, по определению угол AOB равен одному радиану.
Для обозначения радианов используют сокращение «рад».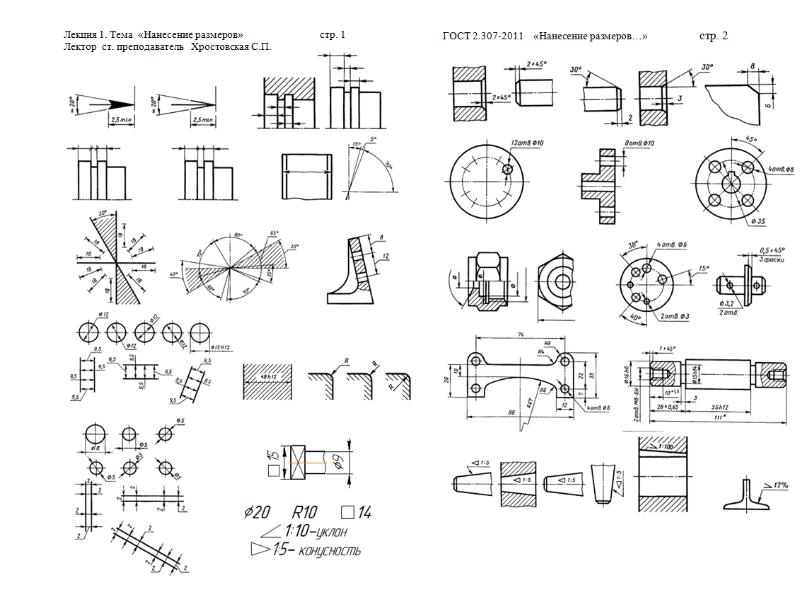 Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.
Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.
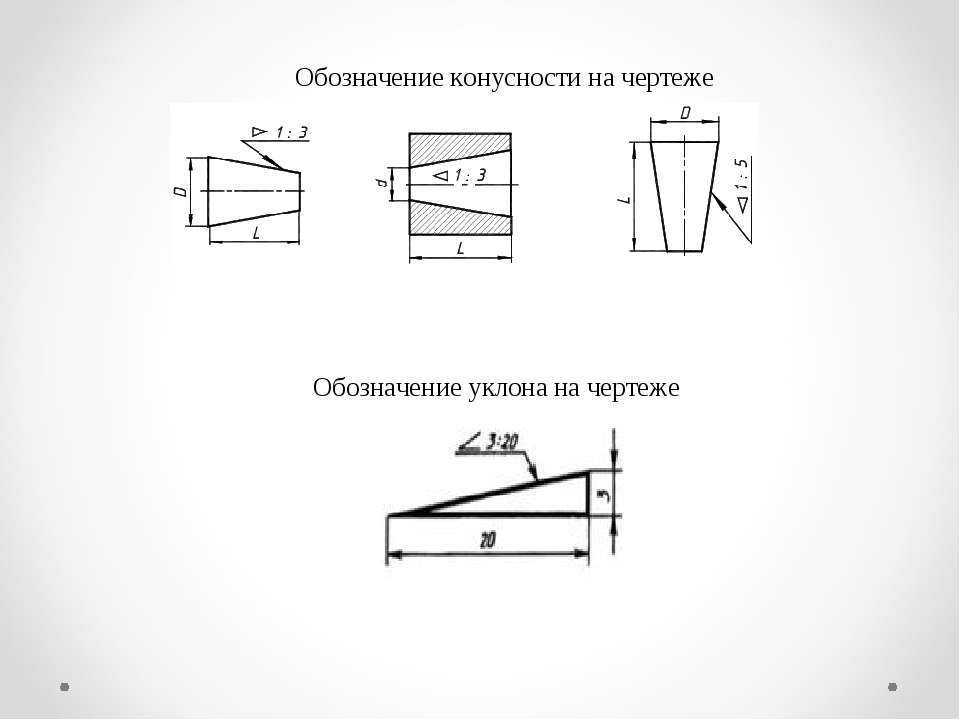
Обозначение углов на чертеже.
На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.
Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.
Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.

- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
Острый угол это угол градусная мера которого до 90 градусов.
Прямой угол это угол градусная мера которого 90 градусов
Тупой угол это угол градусная мера которого больше 90 градусов. Острый угол – это угол меньше 90°. Тупой угол – это угол больше 90°, но меньше 180°. Прямой угол – это угол = 90°.
20. Какие углы называются смежными? Чему равна их сумма?
Смежные углы – два угла с общей вершиной, одна из сторон которых – общая, а оставшиеся стороны лежат на одной прямой (не совпадая) . Сумма смежных углов равна 180°. Или
Два угла называются смежными , если у них одна сторона общая, а другие стороны являются дополнительными лучами. сумма смежных углов равна 180°. Каждый из этих углов дополняет другой до развернутого угла.
21. Какие углы называются вертикальными? Каким свойством они обладают?
Вертикальные
углы – два угла, у которых стороны одного
являются продолжениями сторон другого. Вертикальные углы равны. (Вертикальными
называются углы, образованные пересекающимися прямыми
и не являющиеся прилегающими друг к
другу, то есть общей стороны у них нет,
но вертикальные углы имеют вершину в
одной точке. Вертикальные углы равны
между собой).
Вертикальные углы равны. (Вертикальными
называются углы, образованные пересекающимися прямыми
и не являющиеся прилегающими друг к
другу, то есть общей стороны у них нет,
но вертикальные углы имеют вершину в
одной точке. Вертикальные углы равны
между собой).
22. Какие прямые называются перпендикулярными? Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла. Или Перпендикулярные прямые это прямые пересекающиеся под углом 90 градусов. Или Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.
23. Объясните,
какой отрезок называется перпендикуляром,
проведенным из данной точки к данной
прямой. Что такое основание перпендикуляра?
называется отрезок прямой, перпендикулярной
к данной, который имеет одним из своих
концов их точку пересечения. Этот конец
отрезка называется основанием
перпендикуляра.Перпендикуляром
к данной прямой называется отрезок прямой, перпендикулярной
к данной, который имеет одним из своих
концов их точку пересечения. Конец
отрезка, лежащий на данной прямой,
называется основанием перпендикуляра.
Конец
отрезка, лежащий на данной прямой,
называется основанием перпендикуляра.
24. Что такое теорема и доказательство теоремы? В математике утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а само рассуждение – доказательством теоремы.
Теоре́ма – утверждение, для которого в рассматриваемой теории существует доказательство (иначе говоря, вывод) . В отличие от теорем, аксиомами называются утверждения, которые, в рамках конкретной теории, принимаются истинными без всяких доказательств или обоснований. Доказательство – это утверждение, объясняющее теорему. Теорема – такая гипотеза, которую требуется доказать;Гипотеза всегда требует доказательства. Доказательство – доводы, подтверждающие действенность, правильность теоремы.
Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла.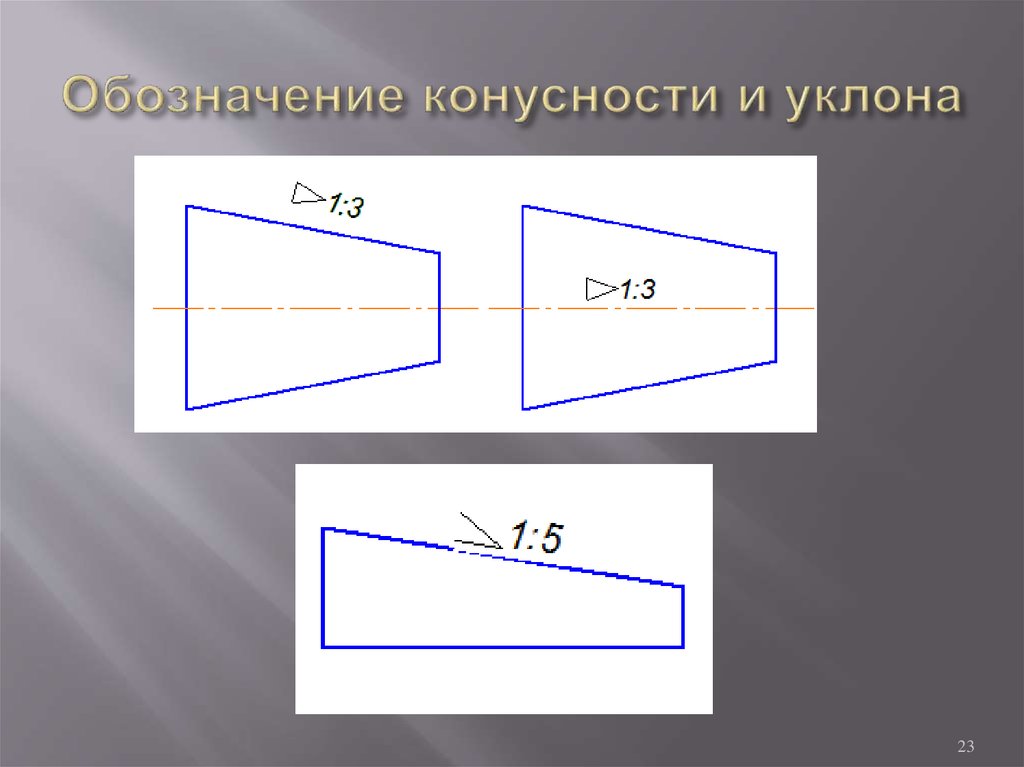 Исходя из этих признаков, мы можем составить определение: угол – геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Исходя из этих признаков, мы можем составить определение: угол – геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре – прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол – это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол – это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие – он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла – от 0 о до 180 о.
Как вы уже поняли, градусная мера выпуклого угла – от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных – острого, тупого, прямого и развернутого – в геометрии существует много других их видов.
определение угла, измерение углов, обозначения и примеры
Очень часто слышу вопрос “Как получитьсимвол галочки в Ворде?” Ответы – один мудренее другого! Проще всего нажать клавишу Альт и, не отпуская её, набрать на боковой цифровой клавиатуре число 10003. Можно так же набрать число 2713 и потом нажать Альт икс. Просто оба эти числа равны между собой: 10003 (десятичное) = 2713 (шестнадцатиричное).
Когда много работаешь в программах Ворд и Ексель, начинаешь понимать, что бросать клавиатуру, хвататься за мышь, а потом снова переходить к “клаве” – неудобно, неэргономично, не… – продолжите сами. Наверное для этого и придуманы разные сочетания кнопок, “горячие” клавиши и т. п. В этом плане мне очень нравится функциональная клавиша F4, нажатие на которую повторяет любое действие, которое только что выполнялось. Например, вам надо 8 слов в разных местах текста выделить полужирным шрифтом. Первое слово вы можете сделать сделать “жирным” щелкнув по букве ” ж ” в меню или нажав одновременно две клавиши Ctrl и b (русская буква и). Для остальных слов достаточно правой рукой щелкнуть мышью по любому месту в нужном слове, а левой рукой нажать клавишу F4. “И так сэм раз”.
п. В этом плане мне очень нравится функциональная клавиша F4, нажатие на которую повторяет любое действие, которое только что выполнялось. Например, вам надо 8 слов в разных местах текста выделить полужирным шрифтом. Первое слово вы можете сделать сделать “жирным” щелкнув по букве ” ж ” в меню или нажав одновременно две клавиши Ctrl и b (русская буква и). Для остальных слов достаточно правой рукой щелкнуть мышью по любому месту в нужном слове, а левой рукой нажать клавишу F4. “И так сэм раз”.
Многие вздрагивают при слове “макрос”, а между тем в них нет ничего страшного и опасного. Вообще, макросы – это очень полезная вещь! Создать макрос в Ворде – проще простого. Допустим, вам часто требуется при наборе текста вставлять название организации: ООО «Рога и Копыта» . Или печатать в конце документа: Исполнитель – Вася Пупкин . Рассмотрим, как набрать первый текст нажатием всего двух клавиш, а второй – одним нажатием на кнопку с любым рисунком, созданную на панели быстрого доступа.
Итак, давайте попробуем: открываем Ворд и выбираем «Сервис-Макросы» или «Вид-Макросы» (в зависимости от того 2003-й или 2007-й) и жмем «Запись макроса…». В появившемся окне можно придумать название макросу и сделать его описание, но можно оставить предложенное по умолчанию название «Макрос1» и ничего не описывать – кому как нравится. Но нажать на значок с изображением клавиатуры или молотка надо обязательно. В первом случае вам будет предложено придумать любое сочетание клавиш, а во втором – кнопку на панели. Для первого текста выбираем сочетание Ctrl+P (что бы легче вспомнить, берем первую букву Рогов), затем нажимаем «Назначить» и «Закрыть». Окно при этом исчезает, а рядом с курсором появляется пиктограмма магнитофонной кассеты, это означает, что «все ходы записываются». В 2003-м Ворде при этом еще появляется малюсенькая плавающая панель. В первый и последний раз (потом это за вас будет делать компьютер) набираем нужный текст с названием фирмы и останавливаем запись. В старом Ворде – просто нажав квадратик на плавающей панели, а в новом – зайдя в меню «Вид-Макросы-Остановить запись». Теперь и всегда (до переустановки Офиса или удаления макроса) нажатие выбранного вами сочетания клавиш выдаст вам то, что вы набрали во время записи макроса.
Теперь и всегда (до переустановки Офиса или удаления макроса) нажатие выбранного вами сочетания клавиш выдаст вам то, что вы набрали во время записи макроса.
Если на начальной стадии вы нажмете на молоток, то в 2003-м появится окно Настройка со стандартным значком макроса, который надо, схватив мышкой, перетащить в любое место верхней панели меню, а затем, щелкнув по кнопке «Изменить выделенный объект» и по строке «Выбрать значок для кнопки» выбрать смайлик или любой понравившийся вам рисунок. Если же нажать на строку «Изменить значок на кнопке…», то откроется простенький графический редактор, в котором можно самому нарисовать значок на свой вкус.
В 2007-м похожий путь: при выборе молотка появляется Настройка панели быстрого доступа, где надо, выделив в левом окошке макрос и нажать кнопку «Добавить». После этого стандартный значок макроса с вашим названием добавится в правое окно, где его можно снова выделить и нажать кнопку «Изменить». Выбор рисунков будет побольше, чем в старом Ворде, но зато убрана возможность нарисовать свой значок и размещать его можно только на панели быстрого доступа.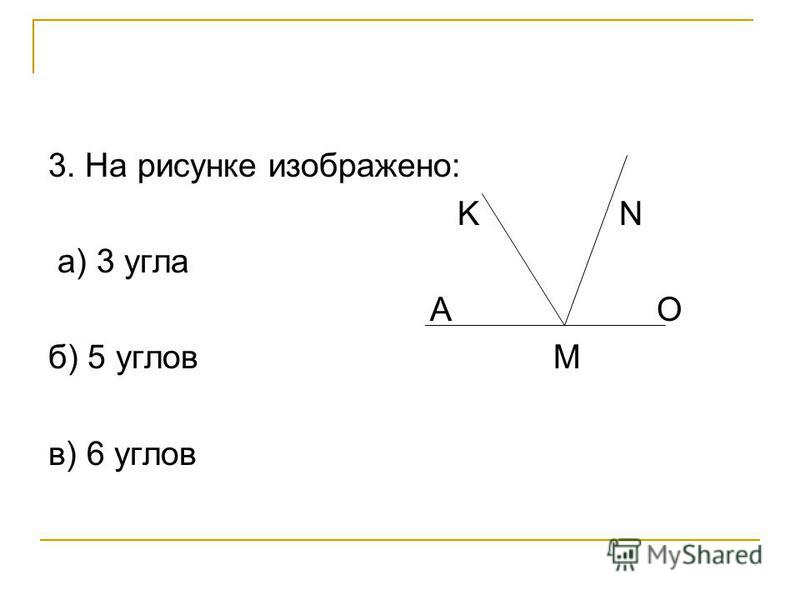
Дальнейшие действия такие же, что и в 2003-м: набор нужного текста и остановка записи. Подобных макросов можно наделать сколько угодно, в результате вы получите возможность одним щелчком по вашему значку (которого, заметьте, нет ни у кого из ваших коллег!) получать нужный текст или любую последовательность операций.
Как и что надо набрать на клавиатуре, чтобы получить в текстовом документе изображение сердечка? Проще всего нажать клавишу Alt и не отпуская её нажать цифру 3 на правой части клавиатуры. Другой способ: набрать число 2665 и нажать сочетание клавиш Alt+х. Так же для получения сердечек можно набрать числа 2765, 2764 или 2661. Очень похожа на сердечко одна из букв грузинского алфавита ღ, получить которую можно набрав код 10Е5 (Е – латинское) и нажав Alt+х.
Вообще для получения любого символа достаточно набрать его
ASCII
-код и нажать
Alt+х.
Например, чтобы напечатать знак доллара «$», проще и быстрее не переходя на английский шрифт набрать число 24, а затем нажать
Alt+х. Можно быстро получить знак суммы «∑»
(код – 2211), символ угла «∠»
(код – 2220), приблизительного равенства
«
≈
»
(код – 2248), различные стрелки и т.д. Именно поэтому иногда вместо слова «собака» говорят «сорок альт икс» имея ввиду @.
Можно быстро получить знак суммы «∑»
(код – 2211), символ угла «∠»
(код – 2220), приблизительного равенства
«
≈
»
(код – 2248), различные стрелки и т.д. Именно поэтому иногда вместо слова «собака» говорят «сорок альт икс» имея ввиду @.
Вот таблица кодов некоторых символов:
Код | Символ | Код | Символ | Код | Символ | Код | Символ |
23 | # | 2020 | † | 2194 | ↔ | 2265 | ≥ |
24 | $ | 2030 | ‰ | 2195 | ↕ | 2640 | ♀ |
26 | & | 2122 | ™ | 2211 | ∑ | 2642 | ♂ |
27 | ” | 2190 | ← | 2220 | 2660 | ♠ | |
40 | @ | 2191 | 2248 | ≈ | 2663 | ♣ | |
60 | ` | 2192 | → | 2260 | ≠ | 2665 | |
394 | Δ | 2193 | ↓ | 2264 | ≤ | 2666 | ♦ |
Если в документах Microsoft Word Вам приходиться работать не только с текстом, но иногда необходимо показать элементарные расчеты, или вставить в текст определенный символ, тогда не найдя его на клавиатуре, Вы зададитесь вопросом: как добавить его в документ?
Сделать это довольно просто, поскольку в текстовом редакторе Ворд есть специальная таблица, в которой Вы точно найдете все необходимое. В данной статье мы с Вами рассмотрим, как, используя ее, можно вставить в документ Ворд примерно равно.
В данной статье мы с Вами рассмотрим, как, используя ее, можно вставить в документ Ворд примерно равно.
Установите курсор в том месте документа, куда будете его добавлять. Затем перейдите на вкладку «Вставка» и в группе «Символы» нажмите на одноименную кнопку. В выпадающем списке выберите пункт «Другие» .
Откроется вот такое окно. В нем в поле «Шрифт» выберите «(обычный текст)» , в поле «Набор» – «математические операторы» . Дальше найдите в списке то, что нужно, кликните по нему и затем нажмите кнопку «Вставить» .
После того, как значок будет добавлен в документ, закройте данное окно, нажав на соответствующую кнопку в правом нижнем углу.
Если Вам часто приходится добавлять в документ различные знаки, которые напечатать напрямую с клавиатуры не получится, и приходится искать их в упомянутой таблице, тогда можете воспользоваться горячими клавишами, для вставки подходящего знака в документ.
Найдите символ в списке и кликните по нему мышкой. Затем внизу в поле «Сочетание клавиш»
посмотрите, какая комбинация для него используется.
Затем внизу в поле «Сочетание клавиш»
посмотрите, какая комбинация для него используется.
В нашем случае, это «2248, Alt+X» . Сначала наберите число «2248» , а потом нажмите «Alt+X» .
Замечу, что не для всех знаков есть сочетания, но его можно назначить самостоятельно, кликнув по кнопке «Сочетание клавиш» .
Если у Вас, как и в примере, знак приблизительно нужно поставить сразу после какой-нибудь цифры, то сочетание получится другое. В примере получилось «32248» .
Поэтому, после того, как Вы нажмете «Alt+X» , может вставится не то, что Вы хотите.
Для того чтобы добавить именно приблизительно-равно, поставьте пробел после той цифры, где он должен стоять и наберите сочетание «2248» . Затем нажимайте «Alt+X» .
Символ будет вставлен. Теперь можно поставить курсив перед добавленным знаком и нажать «Backspace» , чтобы удалить пробел.
Вот так, используя один из способов, можно поставить значок приблизительно равно в документ Ворд.
Оценить статью:
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.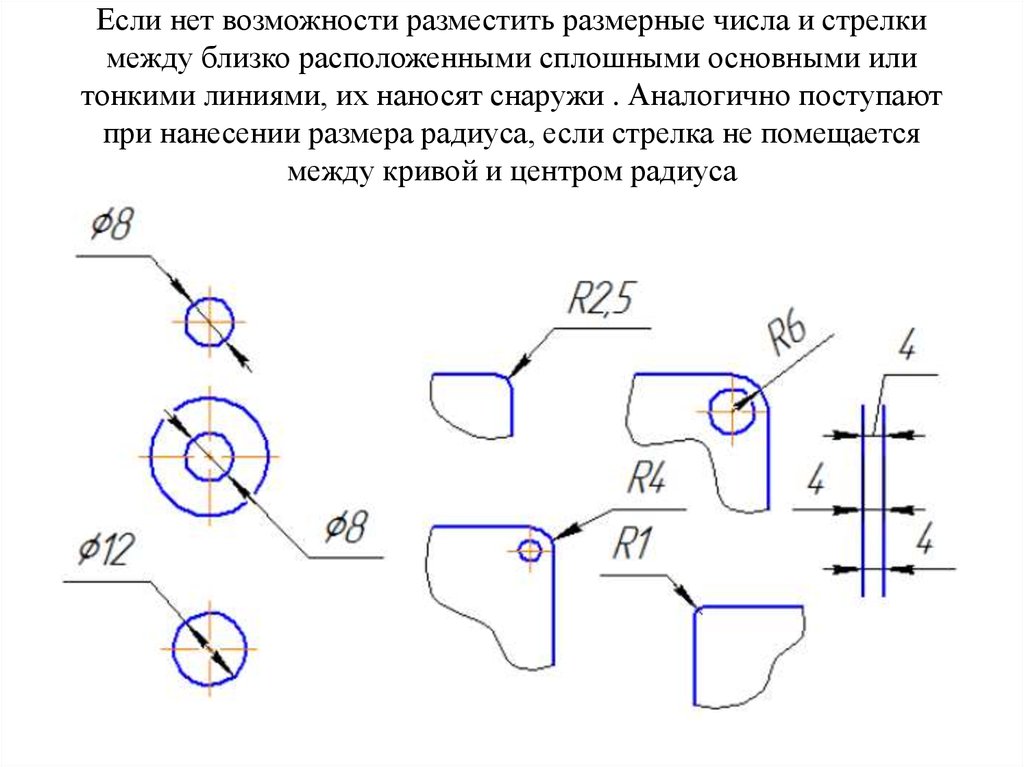
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной – ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение 6
Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.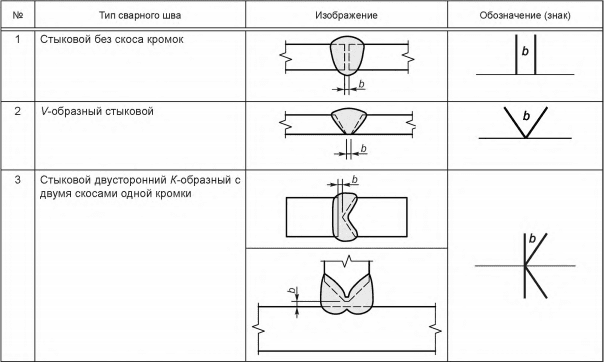
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус .
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « ” », а секунды « “” ». Имеет место обозначение:
1 ° = 60 ” = 3600 “” , 1 ” = (1 60) ° , 1 ” = 60 “” , 1 “” = (1 60) ” = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 ” 59 “” .
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 ” 59 “” . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ.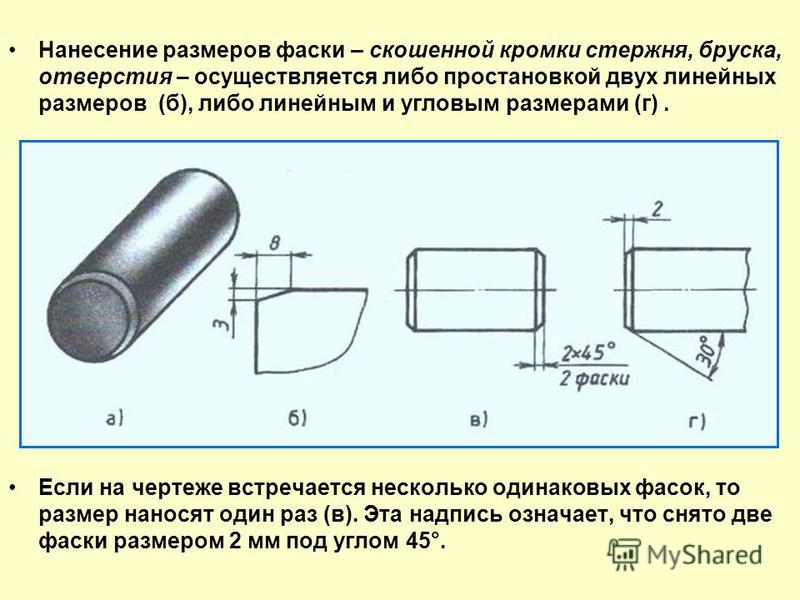 Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.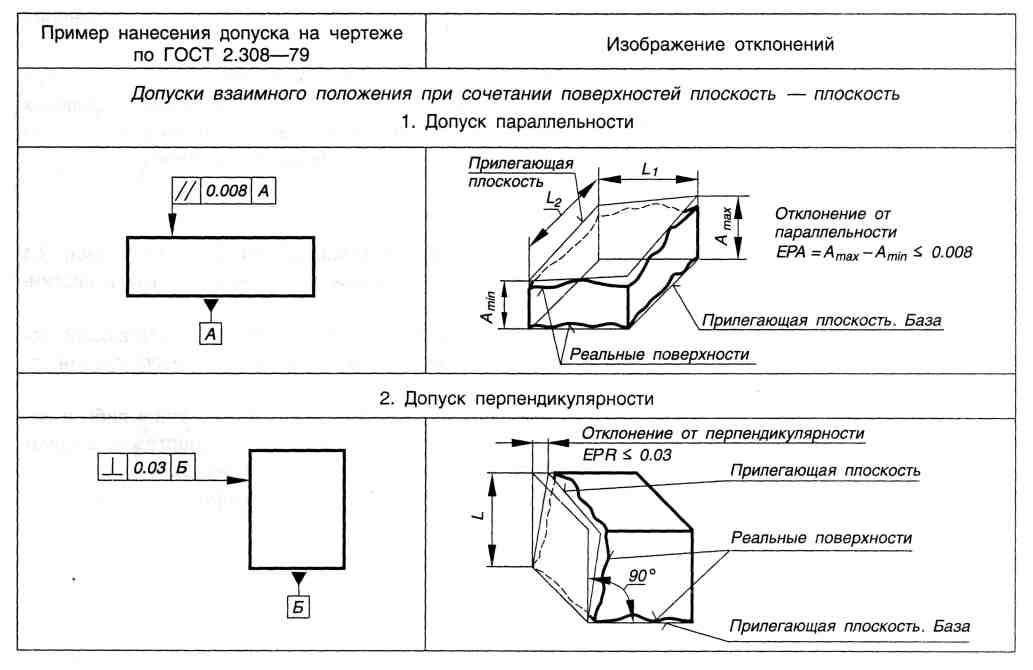
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Навигация по странице.
Определение угла.
Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.
Дадим сначала определение луча.
Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a
. Пусть O
– некоторая точка прямой a
. Точка O
разделяет прямую a
на две части. Каждая из этих частей вместе с точкой О
называется лучом , а точка О
называется началом луча . Еще можно услышать, что луч называют полупрямой .
Каждая из этих частей вместе с точкой О
называется лучом , а точка О
называется началом луча . Еще можно услышать, что луч называют полупрямой .
Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p или луч k ), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА или луч СD ). Покажем изображение и обозначение лучей на чертеже.
Теперь мы можем дать первое определение угла.
Определение.
Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым .
Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.
Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k
, а другая h
), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA
, а вторая сторона угла OB
), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ). Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая – внешней.
Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.
Определение внутренней области угла приводит нас ко второму определению угла.
Определение.
Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.
Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Дадим еще определения смежных и вертикальных углов.
Определение.
Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.
Из определения следует, что смежные углы дополняют друг друга до развернутого угла.
Определение.
Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.
На рисунке изображены вертикальные углы.
Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.
Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными .
Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол).
Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение углов.
Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.
Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градус .
Определение.
Один градус – это угол, равный одной сто восьмидесятой части развернутого угла.
Градус обозначают символом «», следовательно, один градус обозначается как .
Таким образом, в развернутом угле мы можем уложить 180 углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180 равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть развернутого угла) и ровно 90 раз (половина развернутого угла).
Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения). Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определение.
Минута – это одна шестидесятая часть градуса.
Определение.
Секунда – это одна шестидесятая часть минуты.
Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600 секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .
Определение.
Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.
Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.
Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110 ), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом . Угол меньший 90 градусов называется острым углом . Угол больший девяноста градусов называется тупым углом . Итак, мера острого угла в градусах выражается числом из интервала (0, 90) , мера тупого угла – числом из интервала (90, 180) , прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла.
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов.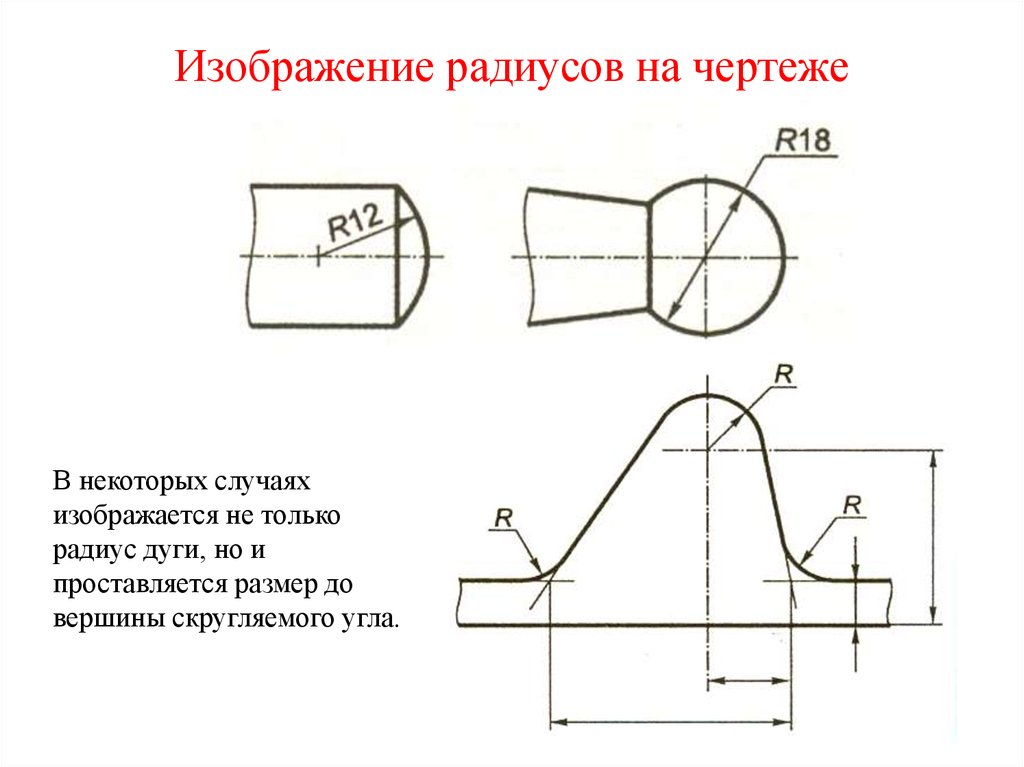 На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол.
Из этого утверждения следует, что . Действительно, если углы АОВ и СОD – вертикальные, то углы АОВ и ВОС – смежные и углы СОD и ВОС также смежные, поэтому, справедливы равенства и , откуда следует равенство .
Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана.
Определение.
Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA (как и радиуса OB ) равна длине дуги AB , поэтому, по определению угол AOB равен одному радиану.
Для обозначения радианов используют сокращение «рад». Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.
Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.
Обозначение углов на чертеже.

На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.
Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.
Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.

- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
Углы в геометрии — введение | 7 класс
Содержание
Если вам приходилось часто ездить по междугородним маршрутам, вполне вероятно, что вы встречали по пути вот это — знак крутого уклона. Водителю он сообщает: «Осторожно! Дорога далее идет под углом». Углы — интересный объект нашего быта. Углы в геометрии — объект не менее интересный, поскольку они одновременно наследуют ряд свойств уже привычных нам фигур: точек и лучей.
Впереди вас ждет раздел, всецело посвященный изучению данной геометрической фигуры и ее особенностей.
Луч и уголСогните свою руку так, будто бы бравируете перед кем-то мускулами. Если рассмотреть полученную в результате фигуру «Мистер Мускул» геометрически, она будет состоять из точки перегиба (локтевого сустава) и двух линий (прямых предплечья и плеча).
Остановимся на прямых и точках. Начертим на плоскости два луча $AB$ и $AB_1$ так, что $AB\cap{AB_1}=A$. Фигура, получившаяся на чертеже ниже, будет называться углом. Видим, что луч и угол взаимосвязаны: углы в геометрии состоят из лучей и точки, общей для этих лучей.
Дадим определение:
Угол — геометрическая фигура, образованная двумя лучами, выходящими из одной начальной точки.
Рассматривать углы в геометрии можно как составную или как в некотором роде «единую» фигуру. Определение, приведенное выше, задает составное понимание фигуры в связке «луч и угол»: луч, еще один луч, точка. Также данную фигуру можно рассмотреть в совокупности. В этом случае лучи будут называться боковыми сторонами, а начальная точка — вершиной угла.
Луч и угол
Сторона и вершина
Угол представляет для нас больший интерес в качестве совокупной фигуры. Изучать его мы будем именно из позиции «вкупе». Однако не забывайте, что любой угол всегда раскладывается на лучи и точку.
Изучать его мы будем именно из позиции «вкупе». Однако не забывайте, что любой угол всегда раскладывается на лучи и точку.
{"questions":[{"content":"[[speech-1]]Угол — это геометрическая фигура, образованная двумя [[fill_choice-5]], выходящими из [[fill_choice-16]].","widgets":{"speech-1":{"type":"speech","text":"Повторим определение. Дополните указанное ниже определение луча наиболее подходящими словами."},"fill_choice-5":{"type":"fill_choice","options":["лучами","прямыми","отрезками"],"answer":0},"fill_choice-16":{"type":"fill_choice","options":["одной начальной точки","двух отличных друг от друга точек"],"answer":0}}}]}
Обозначение углаУильям Отред, английский математик XVI–XVII вв. Придумал логарифмическую линейку, знак деления («$/$»), знак умножения («$\times$»). Также «облагородил» обозначение угла: спасибо мистеру Отреду, что угол мы обозначаем символом «$\angle$», а не знаком неравенства.
Существует несколько вариантов того, как в математической нотации дается обозначение угла. Все варианты объединяет использование символа «$\textcolor{coral}{\angle}$», — этому символу, кстати, больше четырехсот лет. Примечательно, что первая его версия от 1634 года напоминала знак неравенства «$<$». Символ указывается перед буквенным обозначением и показывает, что далее речь пойдет о фигуре «угол».
❗ Почему знаки обозначения фигур важны и нужны
Забегая немного вперед, покажем одну из особенностей обозначения угла способом «три точки». Делается это следующим образом: «$\angle{ABC}$». Тремя точками в том числе обозначается треугольник: «$\bigtriangleup{ABC}$».
Если не указывать перед буквами знак фигуры, создается неоднозначность. Вот почему знаки обозначения фигур крайне важны, когда речь идет про углы в геометрии. Не забывайте обозначать фигуры.
Обозначение угла через вершинуОбозначить углы в геометрии можно с помощью всего лишь одной буквы — той, что определяет точку вершины. Рассмотрим чертеж, где точка $A$ является вершиной. Данный угол обозначается как $\angle{A}.$
Рассмотрим чертеж, где точка $A$ является вершиной. Данный угол обозначается как $\angle{A}.$
А вы про какой угол?
Это наиболее экономный способ записи, однако он не всегда удобен из-за возможной неоднозначности. Например, ситуация на чертеже: точка $A$ здесь является общей для трех лучей. И что, «$\angle{A}$» — это про тот, что слева, или тот, что справа?
Выбирать обозначение угла важно так, чтобы по ходу решения задачи или доказательства всем было ясно, где располагается указываемый вами угол.
Обозначение угла строчными греческими буквамиДабы избежать неопределенности, на чертеж иногда наносят отдельную букву. Исторически сложилось, что букву эту выбирают из греческого алфавита строчного регистра.
На представленном чертеже примером такого обозначения будет «$\angle{\alpha}$».
| Буква | Как обозначается | Как читается |
| $\alpha$ | $\angle{\alpha}$ | «угол альфа» |
| $\beta$ | $\angle{\beta}$ | «угол бета» |
| $\gamma$ | $\angle{\gamma}$ | «угол гамма» |
| $\delta$ | $\angle{\delta}$ | «угол дельта» |
| $\theta$ | $\angle{\theta}$ | «угол тета» |
| $\phi$ | $\angle{\phi}$ | «угол фи» |
{"questions":[{"content":"Упражнение для запоминания названий букв греческого алфавита. Не подсматривайте в таблицу выше и попытайтесь распределить буквы согласно их названию на русском самостоятельно. [[matcher-1]]","widgets":{"matcher-1":{"type":"matcher","labels":["$\\alpha$","$\\beta$","$\\gamma$","$\\delta$","$\\phi$","$\\theta$"],"items":["альфа","бета","гамма","дельта","фи","тета"]}}}]}Обозначение угла с помощью направляющих точекВспомним, что луч можно обозначать не только с помощью начальной, но и направляющей точки. Рассмотрим лучи, пересекающиеся в точке $A$: $AB\cap{AC}=A$. Направляющими точками лучей являются точки $B$ и $C$.
Обозначаться данный угол будет как $\angle{CAB}$. Порядок наоборот также допустим: $\angle{BAC}$.
При способе обозначения «три точки» точка, указанная посередине, всегда является вершиной угла, а боковые буквы в записи являются точками, лежащими на сторонах угла.
Последний способ, наименее распространенный, — использовать прямые для обозначения угла. Луч является частью прямой, и если на чертеже имеется дополнительное буквенное указание прямых, их можно записать в порядке против часовой стрелки через скобки. Например, $\angle{(ab)}$.
Как и с точками, вариант «наоборот» допустим — $\angle{ba}$.
{"questions":[{"content":"[[image-1]] Проверим вас задачкой посложнее. Дана пирамида. Ее основанием является треугольник — фигура, состоящая из трех углов. Как будет обозначаться угол основания, вершина которого выделена красным цветом? [[choice-6]]","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/08/TFM.svg"},"choice-6":{"type":"choice","options":["$\\angle{TFM}$","$\\angle{FTM}$","$\\angle{TMF}$"],"answer":[0]}}}]}Дополнительно об обозначении углов
Скрыть содержимое
Порядок решает
Угол из примера в разделе «Обозначение угла с помощью направляющих точек».
И порядок этот — от точки слева к точке справа. Еще одна данность, как и буквы греческого алфавита: углы в геометрии принято отсчитывать против часовой стрелки. Поэтому угол обозначен в первую очередь как «$\angle{CAB}$», не «$\angle{BAC}$».
Вариант по направлению часовой стрелки («$\angle{BAC}$») допустим.
То, что принято, вовсе не обязательно. Просто правило хорошего тона, которое, если того требует удобство, можно нарушить.
Углы в геометрии: определение направления против часовой стрелки
Если вам сложно представлять поворот стрелки при обозначении углов, можно воспользоваться простым методом пальцев. Алгоритм прост:
👉 приложите указательный палец левой руки к крайней точке угла с левой стороны;
👈 приложите указательный палец правой руки к крайней точке угла с правой стороны;
✌️ точка вершины угла должна располагаться посередине;
✍️ запишите буквенное обозначение точек слева направо — от пальца левой руки к пальцу правой руки.
Пример
Значения не имеет, как при этом расположен угол на плоскости. Рассмотрим, к примеру, положение угла «домиком». Соответствующий угол будет обозначаться как $\angle{MPK}$.
Еще пример
Углы в геометрии:
внешняя сторона углаУгол образует на плоскости две области — внутреннюю область и внешнюю. Определяя углы в геометрии, мы, как правило, оцениваем фигуру, полученную во внутренней области. Однако стороны угла можно рассматривать как для внутренней области, так и для внешней. С учетом, что существует так называемая внешняя сторона угла, лучи соответственно образуют два угла: внутренний и наружный.
Области угла
Внешняя сторона угла
Параллельное по тексту обозначение и внутреннего, и наружного углов часто сопряжено с проблемой неоднозначности. Решить ее можно двумя способами — простым и не очень простым. Если вы ознакомились с содержанием скрытого блока о методе пальцев, предлагаем также ознакомиться с не очень простой альтернативой ниже.
- Простой. Наносить на чертеж буквенное обозначение углов ($\alpha$, $\beta$, $\gamma$). Скажем, если внутренний угол обозначить как «$\angle{\theta}$», соответствующий наружный удобно обозначить как «$\angle{\theta_1}$».
Альтернативный способ
Скрыть содержимое
- Не очень простой. Использовать обозначение «три точки» или с помощью прямых, однако при этом держать строгий порядок: против часовой — для внутренних, по часовой — для соответствующих наружных.
Например, $\angle{ABC}$ и $\angle{CBA}$. Или $\angle{(ab)}$ и $\angle{(ba)}$.
{"questions":[{"content":"[[image-1]]<i>Подведем итоги практически. На чертеже даны два луча, образующие внутренний и наружный углы. Распределите данные ниже обозначения в строгой нотации (<b>против часовой стрелки</b>) согласно предложенным углам.</i>[[grouper-22]]","widgets":{"image-1":{"type":"image","url":"https://obrazavr. ru/wp-content/uploads/2022/08/test.svg"},"grouper-22":{"type":"grouper","labels":["Внутренний угол","Наружный угол"],"items":[["$\\angle{\\alpha}$","$\\angle{CAB}$","$\\angle{(ab)}$","$\\angle{A}$"],["$\\angle{\\phi}$","$\\angle{BAC}$","$\\angle{(ba)}$"]]}}}]}
ru/wp-content/uploads/2022/08/test.svg"},"grouper-22":{"type":"grouper","labels":["Внутренний угол","Наружный угол"],"items":[["$\\angle{\\alpha}$","$\\angle{CAB}$","$\\angle{(ab)}$","$\\angle{A}$"],["$\\angle{\\phi}$","$\\angle{BAC}$","$\\angle{(ba)}$"]]}}}]}{"questions":[{"content":"[[image-1]]Выберите из предложенных вариантов ниже обозначения, подходящие указанному на чертеже углу. [[choice-8]]","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/08/test1-1.svg"},"choice-8":{"type":"choice","options":["$\\angle{\\alpha}$","$\\angle{CAB}$","$\\angle{ab}$","$\\angle{A}$","$\\angle{C_1{AB}}$"],"answer":[0,1,2]}}}]}углов и линий
углов и линий Вернуться к оглавлениюОбзор урока
- Солнечные часы, гномоны, затмения и транзиты
- Уголки: основные, попарно, В относительных позициях, Из тригонометрии (справочная, центральная, вписанная)
- Предположения: действительные и неверные
- Алгебраические свойства
- Линии: параллельные и перпендикулярные
- Аргументы доказательства: почему, абзац и два столбца
- Правила построения, черчения, черчения
- Лабиринты и лабиринты
Солнечные часы, гномоны, затмения и транзиты
Астрономические события определяют день, лунный месяц и год. Когда человек хотел разделить день, солнечные часы оказались полезными.
Здесь
вы найдете занятия по геометрии на тему солнечных часов.
Существует множество вариаций на тему солнечных часов.
Однако одно словарное слово из этого числа равно 9.0024 гномон ,
часть солнечных часов, отбрасывающая тень.
Какой правильный угол для горизонтальных солнечных часов?
это делает с горизонтом?
Посещение здесь может быть полезным.
Когда человек хотел разделить день, солнечные часы оказались полезными.
Здесь
вы найдете занятия по геометрии на тему солнечных часов.
Существует множество вариаций на тему солнечных часов.
Однако одно словарное слово из этого числа равно 9.0024 гномон ,
часть солнечных часов, отбрасывающая тень.
Какой правильный угол для горизонтальных солнечных часов?
это делает с горизонтом?
Посещение здесь может быть полезным.Другое исследование углов включает затмения и транзиты. Предполагается, что учащийся знаком с такими событиями, особенно, пара Венеры проходит в июне 2004 и 2012 гг. достаточно, чтобы никто из живых не видел ни одного.
Основные углы
| Угол – это объединение двух лучей с одним концом. |
Лучи, образующие угол, являются его сторонами .
Вершина является общим концом двух лучей.
Символ угла () можно легко спутать с символом
менее чем (<). Одна важная классификация углов основана на их угловой мере .
Углы обычно измеряются либо в градусов или радиан .
(См. также введение в Числа, урок 11.)
Иногда мы видим ссылки на оценку (1 оценка = 0,9°).
Хотя некоторые (наш текст) опускают символ градуса, мы не ожидаем, что вы когда-либо сделаете это.
360° или 2 радиана в
полный оборот или круг.
Важно различать угол (набор точек) и
его мера обозначается m.
Нулевой угол – это когда два луча имеют одни и те же точки и
совпадают. Таким образом, они кажутся одним лучом.
Он назван так из-за его нулевой угловой меры. острый угол – это угол, градусная мера которого лежит строго между 0 и 90°.
Прямой угол — это угол, градусная мера которого равна точно 90°.
На чертеже символ
может использоваться для обозначения двух лучей или сегментов как перпендикулярных (под прямым углом).
В символах мы пишем, что одна линия или отрезок перпендикулярны другому, используя
символ .
Одна важная классификация углов основана на их угловой мере .
Углы обычно измеряются либо в градусов или радиан .
(См. также введение в Числа, урок 11.)
Иногда мы видим ссылки на оценку (1 оценка = 0,9°).
Хотя некоторые (наш текст) опускают символ градуса, мы не ожидаем, что вы когда-либо сделаете это.
360° или 2 радиана в
полный оборот или круг.
Важно различать угол (набор точек) и
его мера обозначается m.
Нулевой угол – это когда два луча имеют одни и те же точки и
совпадают. Таким образом, они кажутся одним лучом.
Он назван так из-за его нулевой угловой меры. острый угол – это угол, градусная мера которого лежит строго между 0 и 90°.
Прямой угол — это угол, градусная мера которого равна точно 90°.
На чертеже символ
может использоваться для обозначения двух лучей или сегментов как перпендикулярных (под прямым углом).
В символах мы пишем, что одна линия или отрезок перпендикулярны другому, используя
символ . Тупой угол — это угол, градусная мера которого лежит строго между 90° и 180°.
Прямой угол — это угол, в котором оба луча противоположны и
образуют [прямую] линию. Его мера составляет 180°.
Не все геометрии принимают нулевые и прямые углы как углы, часто
указав, что составляющие лучи должны быть неидентичными и непротивоположными.
Еще два угловых члена
угол рефлекса
для углов от 180° до 360° и
полный угол
или 360° (один оборот).
Углы иногда могут быть названы только по их вершине.
(А),
но так как более чем один угол часто имеет общую вершину, это “псевдоним”
может быть неоднозначным и полная спецификация с использованием трех пунктов
(ВАС), таким образом, необходимо.
В других случаях углы могут быть обозначены цифрами (см. ниже).
Тупой угол — это угол, градусная мера которого лежит строго между 90° и 180°.
Прямой угол — это угол, в котором оба луча противоположны и
образуют [прямую] линию. Его мера составляет 180°.
Не все геометрии принимают нулевые и прямые углы как углы, часто
указав, что составляющие лучи должны быть неидентичными и непротивоположными.
Еще два угловых члена
угол рефлекса
для углов от 180° до 360° и
полный угол
или 360° (один оборот).
Углы иногда могут быть названы только по их вершине.
(А),
но так как более чем один угол часто имеет общую вершину, это “псевдоним”
может быть неоднозначным и полная спецификация с использованием трех пунктов
(ВАС), таким образом, необходимо.
В других случаях углы могут быть обозначены цифрами (см. ниже).
Пары уголков
Углы часто идут парами, которые могут иметь специальные имена. в зависимости от их относительного размера или местоположения. Смежные углы — это углы, имеющие общую сторону или луч. Пара дополнительных углов в сумме дает 90°.
Пара дополнительных углов в сумме составляет 180°.
Линейная пара углов является одновременно и дополняющей, и смежной. Вертикальные углы имеют общую вершину и образованы продолжением
каждый луч через вершину. Буква X дает некоторые
хорошие примеры. Угол открытия вверх и угол открытия вниз
являются вертикальными углами, как и пара, открывающаяся влево и вправо.
Вертикальные углы обладают легко доказываемым свойством, приведенным ниже.
Вы можете доказать это свойство, заметив, что эти два угла равны
дополнение к тому же углу.
Пара дополнительных углов в сумме дает 90°.
Пара дополнительных углов в сумме составляет 180°.
Линейная пара углов является одновременно и дополняющей, и смежной. Вертикальные углы имеют общую вершину и образованы продолжением
каждый луч через вершину. Буква X дает некоторые
хорошие примеры. Угол открытия вверх и угол открытия вниз
являются вертикальными углами, как и пара, открывающаяся влево и вправо.
Вертикальные углы обладают легко доказываемым свойством, приведенным ниже.
Вы можете доказать это свойство, заметив, что эти два угла равны
дополнение к тому же углу.| Вертикальные углы равны. |
Углы делят свою плоскость на три области: угол; область внутри или внутренняя до угла; и область снаружи или снаружи до угла. Для углов измерения от 0° до 180°, внутренность — выпуклое множество. Луч, идущий из вершины угла через внутреннюю часть такой, что он делит угол на два конгруэнтных (одинаковая форма и мера) углов называется биссектриса угла.
 Биссект означает разрезать на две равные части.
Биссект означает разрезать на две равные части. Углы в относительных положениях
Углы также образуются, когда поперечная пересекает пару прямых, которые не обязательно параллельны. Типичным примером может быть не равный символ: . Углы, находящиеся в том же относительном положении, но на другой прямой, называются соответствующие углы (углы 1 и 5 на рисунке внизу справа). Слово альтернативный часто используется для обозначения вещей на противоположные стороны, как некоторые листья на стебле. В данном контексте это означает на противоположных сторонах трансверсали. Слово интерьер относится к области между линиями, тогда как слово внешний вид относится к областям вне линий. Мы называем эти углы между линиями внутренними . углы (углы 3, 4, 5 и 6) и находящиеся вне линии как внешних угла (углы 1, 2, 7 и 8). (Обратите внимание также на использование inner/ внешние углы применительно к многоугольникам. )
Таким образом, когда у нас есть поперечное сечение двух линий (не обязательно параллельных)
у нас есть альтернативных внутренних угла (углы 4 и 6 внизу справа)
и альтернативные внешние углы (углы 1 и 7 внизу справа).
Если пара прямых параллельна, мы имеем следующие важные свойства.
)
Таким образом, когда у нас есть поперечное сечение двух линий (не обязательно параллельных)
у нас есть альтернативных внутренних угла (углы 4 и 6 внизу справа)
и альтернативные внешние углы (углы 1 и 7 внизу справа).
Если пара прямых параллельна, мы имеем следующие важные свойства. Две прямые, пересеченные секущей, параллельны тогда и только тогда, когда:
|
Угол между двумя сторонами многоугольника равен внутренних углов ,
тогда как угол, образованный одной стороной и продолжающий другую сторону
угол в многоугольнике равен экстерьер угол.
Они образуют линейную пару.
Примеры внутренних углов: x и 60 º .
на рисунке слева.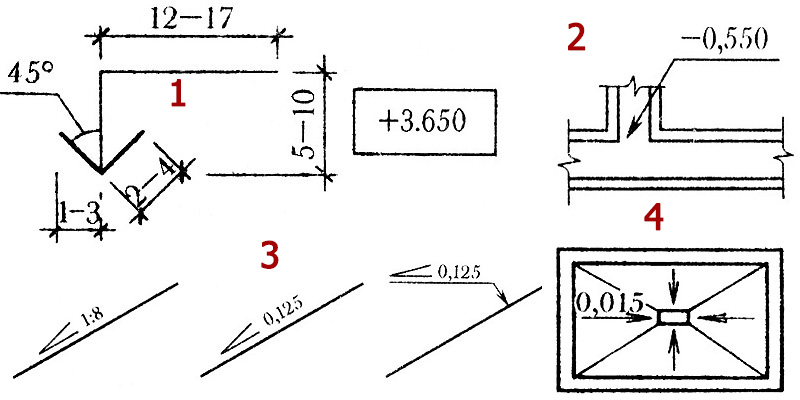 Угол обозначен (2 x +4) º является внешним углом.
Мы также можем различать внутреннюю и внешнюю часть многоугольника.
отметив, что ваша правая сторона обращена внутрь, когда вы путешествуете по часовой стрелке вокруг закрытой фигуры или слева от вас во время движения против часовой или против часовой как говорят на
другая сторона «пруда».
Угол обозначен (2 x +4) º является внешним углом.
Мы также можем различать внутреннюю и внешнюю часть многоугольника.
отметив, что ваша правая сторона обращена внутрь, когда вы путешествуете по часовой стрелке вокруг закрытой фигуры или слева от вас во время движения против часовой или против часовой как говорят на
другая сторона «пруда».
Углы из тригонометрии
Есть также углы, которые особенно важны в тригонометрии. Во-первых, в тригонометрии вершина угла находится в начале координат. система координат с одним лучом, совпадающим с осью x . Затем углы измеряются как положительных , если они измерены. против часовой стрелки от x – ось или как минус , если измерять по часовой стрелке от оси x . Это называется стандартной позицией . Наша геометрия различает поворота и угла. Так, в тригонометрии углы могут быть больше 180° или меньше 0°, тогда как в геометрии могут быть только повороты. Опорный угол является острым (или прямым) углом между
луч и ось x .
Всегда между 0° и 90° включительно.
Угол в стандартном положении равен квадрантному углу всякий раз, когда
его конечная сторона лежит на оси.
Таким образом, квадрантные углы кратны 90°. Сотерминальные углы — это углы, имеющие общие стороны,
например, 120° и -240° или 90° и 450°.
Котерминальные углы отличаются на целое кратное
360° или 2 радиана.
Углы внутри окружностей равны либо центральным углам, либо , если их вершина
это центр круга, или вписанных угла если их вершина
находится на круге. (Мы предполагаем, что каждая сторона включает в себя точку на окружности другой
чем вершина.)
Центральный угол пересекает часть окружности окружности
называется дугой .
Дуга является малой дугой , если ее центральный угол меньше 180°.
Дуга является большой дугой , если ее центральный угол больше 180°.
Если дуга составляет ровно 180°, она называется полуокружностью .
Опорный угол является острым (или прямым) углом между
луч и ось x .
Всегда между 0° и 90° включительно.
Угол в стандартном положении равен квадрантному углу всякий раз, когда
его конечная сторона лежит на оси.
Таким образом, квадрантные углы кратны 90°. Сотерминальные углы — это углы, имеющие общие стороны,
например, 120° и -240° или 90° и 450°.
Котерминальные углы отличаются на целое кратное
360° или 2 радиана.
Углы внутри окружностей равны либо центральным углам, либо , если их вершина
это центр круга, или вписанных угла если их вершина
находится на круге. (Мы предполагаем, что каждая сторона включает в себя точку на окружности другой
чем вершина.)
Центральный угол пересекает часть окружности окружности
называется дугой .
Дуга является малой дугой , если ее центральный угол меньше 180°.
Дуга является большой дугой , если ее центральный угол больше 180°.
Если дуга составляет ровно 180°, она называется полуокружностью .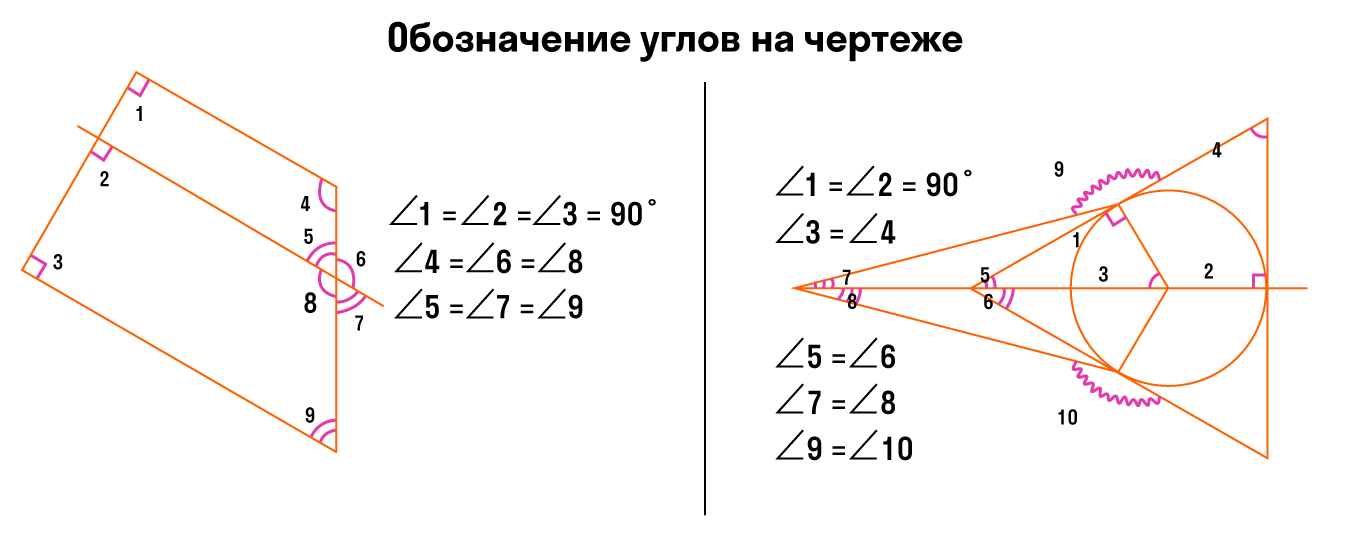 Второстепенные дуги задаются двумя точками (буквами) под кривой линией,
тогда как полуокружности и большие дуги задаются с помощью трех точек.
Между центральным
угол и соответствующий ему вписанный угол.
Второстепенные дуги задаются двумя точками (буквами) под кривой линией,
тогда как полуокружности и большие дуги задаются с помощью трех точек.
Между центральным
угол и соответствующий ему вписанный угол.| Вписанный угол равен половине центрального угла, опирающегося на ту же дугу. |
Если вы знаете величину центрального угла, вы также можете вычислить его длина дуги как пропорция между этой мерой над 360° равны этой неизвестной длине дуги по окружности.
Предположения: действительные и неверные
В геометрии мы никогда ничего не принимаем как должное, но накапливайте знания, доказывая все шаг за шагом. Эта традиция восходит к древнегреческой Пифагорейская школа и был кодифицирован много лет спустя Евклидом в 13-томном наборе книг под названием Элементы . Доказательства часто идут наперекосяк, потому что шаги выполняются в неправильном порядке.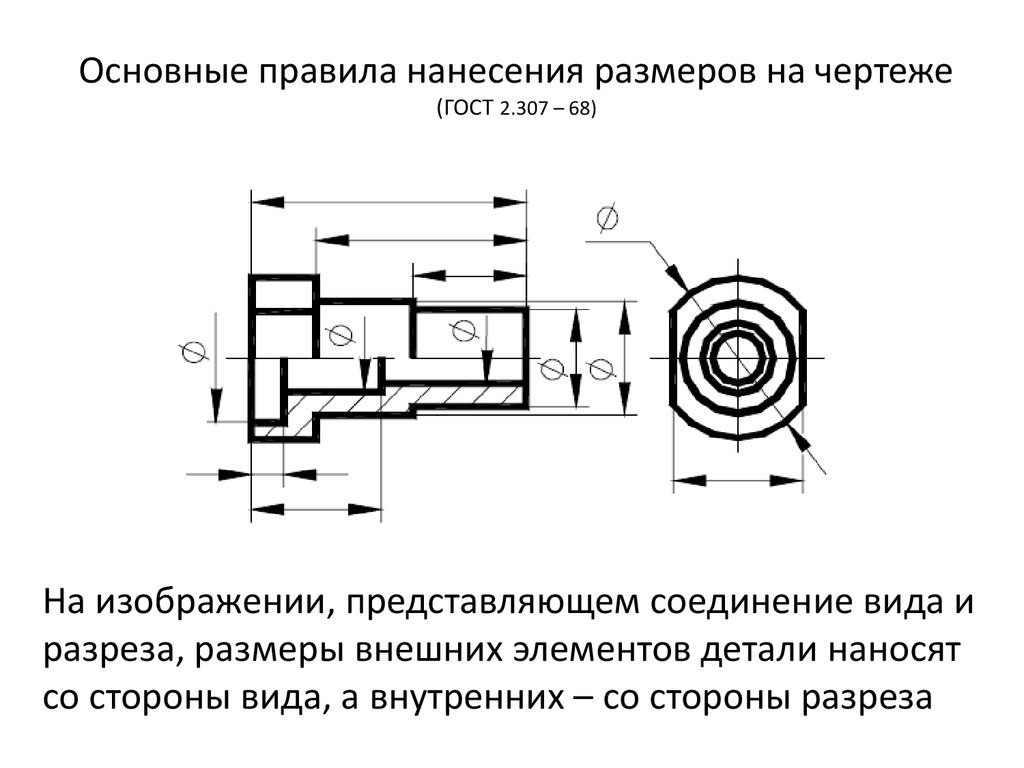 или шаги пропущены.
Еще одна распространенная ошибка — делать неправильные предположения.
или не должным образом поддерживают предположения.
Пожалуйста, ознакомьтесь со следующими списками!
или шаги пропущены.
Еще одна распространенная ошибка — делать неправильные предположения.
или не должным образом поддерживают предположения.
Пожалуйста, ознакомьтесь со следующими списками! Следующие позиции можно принять за из рисунков:
|
Следующие позиции нельзя принять за из рисунков:
|
Всегда помните: геометрические диаграммы рисуются не в масштабе.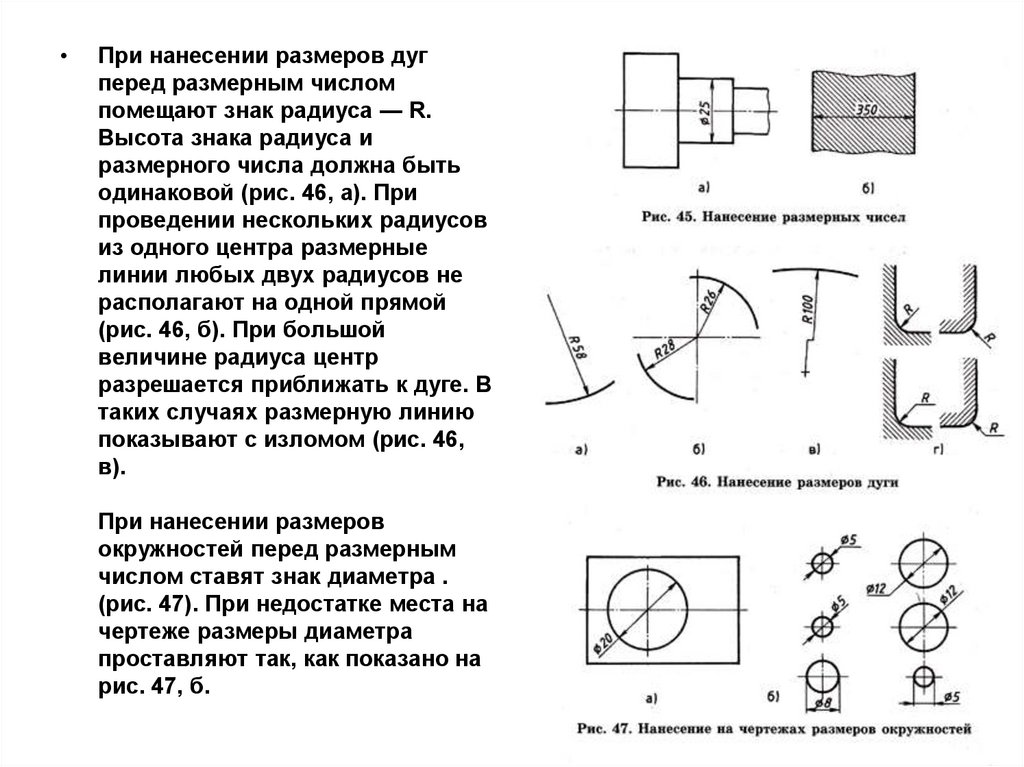 |
Алгебраические свойства
Хотя мы представили много аксиом о действительных числах ранее в уроке чисел 13 мы рассмотрим и снова обобщил их здесь, поскольку они применимы к нашей геометрии.| Постулаты равенств, неравенств и действий: | Пример: | |
|---|---|---|
| Рефлексивное | х = х . | |
| Симметричный | Если х = y , то y = х . | |
| Транзитив | Если x = y и y = z , то x = 2 z . | |
| Свойство равенства сложения | Если x = y , тогда х + z = y + z . | |
| Свойство равенства умножения | Если x = y , то x x z = y x z . | |
| Свойство равенства неравенству | Если x и y >0 и x + y = z 1 , то z 2 3 > | 131 x и z > y .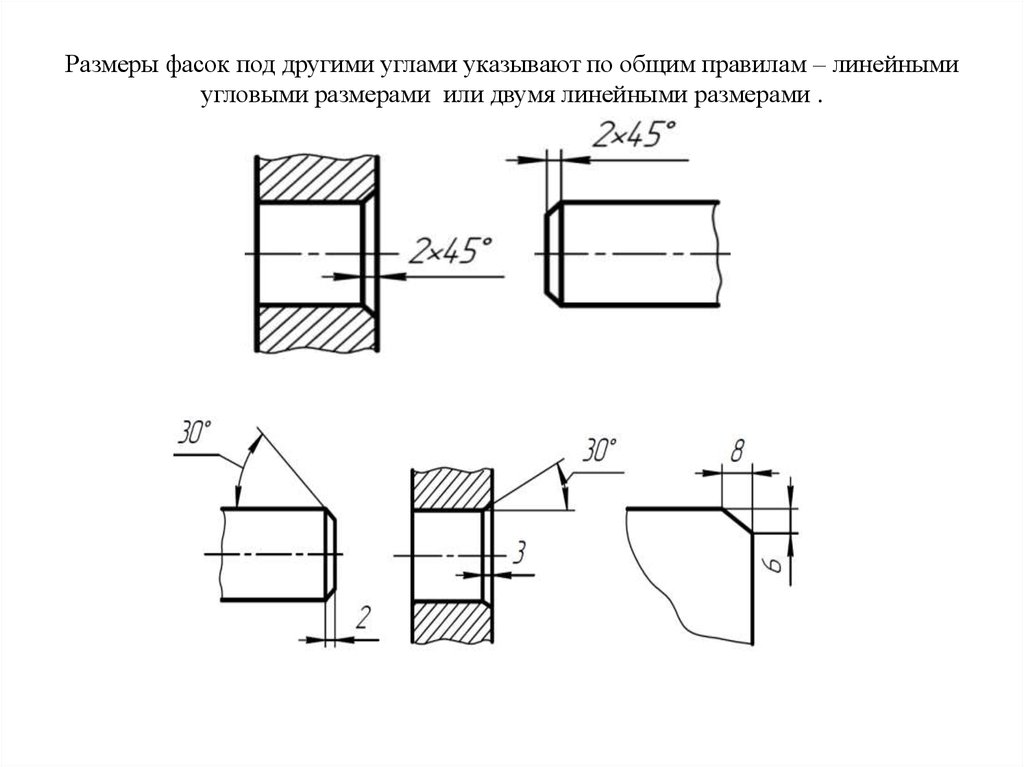 |
| Свойство замены | Если x = y , то x можно заменить на y в любом месте. |
Простой способ различать рефлексивные, симметричные и транзитивные
свойство состоит в том, чтобы связать буквенную последовательность RST с числовой
последовательность 123 и обратите внимание на количество переменных, используемых в каждом определении.
Вычитание было определено с помощью аддитивных инверсий
и деление также определялось с помощью мультипликативных инверсий
(Числа Урок 2).
Следовательно, приведенные выше свойства сложения и умножения позволяют
операции также.
Кроме того, аналогичные свойства для неравенств (< и >, но не
)
для переходного, сложения,
и умножение (на z >0) справедливы и вышеизложенные постулаты.
Предпоследнее свойство, приведенное выше, очень похоже на свойство
Неравенство треугольника. Освоение алгебры является основной темой геометрии,
как наращивание словарного запаса, разработка важных понятий,
и обострение критического мышления. Нанесение линий и неравенств на координатную плоскость,
нахождение уклона, определение параллельности или перпендикулярности,
являются основным местом для развития этого математического мастерства.
Нанесение линий и неравенств на координатную плоскость,
нахождение уклона, определение параллельности или перпендикулярности,
являются основным местом для развития этого математического мастерства.
Строки
Мы представили ранее (Числа Урок 12) определение наклона и различные формы линейных уравнений, особенно у = м х + б , где м — уклон, а b — точка пересечения y .| Если две прямые параллельны, то их наклоны равны. Если две прямые перпендикулярны, то произведение их наклонов равно -1. |
Числа, произведение которых равно -1, называются 9.0024 отрицательные реципроки. Если наклон одной линии – x , а наклон другой 1/ x ,
тогда – х 1 / х = -1.
Перпендикулярные линии, конечно, всегда образуют углы 90°.
Другими терминами для перпендикулярно являются: ортогональный , нормальный ,
и, конечно же, справа.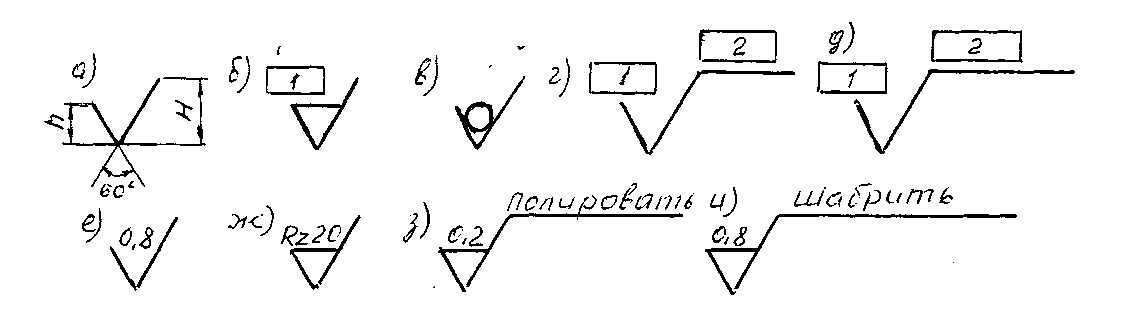
Свойство транзитивности может использоваться для отображения двух линий, параллельных третья линия параллельна друг другу. Это часто называют Транзитивность параллелизма Теорема . Если две прямые перпендикулярны одной прямой, то две прямые параллельны друг другу, если они компланарны. Если прямая перпендикулярна прямой, параллельной другой, то первая линия перпендикулярна двум другим, опять же, если они все компланарны. Евклидова или плоская геометрия, которую мы изучаем, делает это основное предположение.
Доказательство
Математические доказательства обычно необходимы по следующим трем причинам. 1) Люди иногда не соглашаются, потому что что-то очевидное для них может быть неочевидным. так очевидно для другого. 2) Неожиданные результаты можно проверить. 3) Некоторые утверждения долгое время не поддаются проверке. Таким образом, возможно, что это не может быть доказано или просто не соответствует действительности.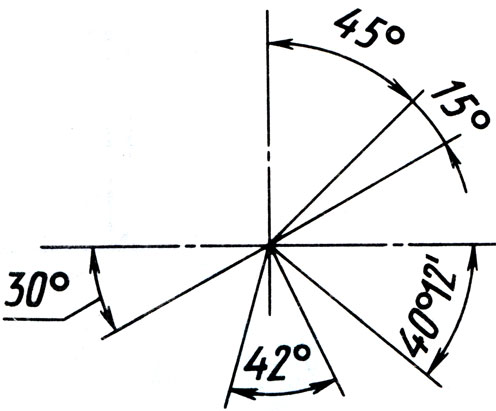
Аргументы доказательства могут быть записаны во многих стилях, так же, как есть много разных стилей написания: эссе, списки понятий, и т.д. Двумя наиболее распространенными формами доказательства являются два столбца и параграф . Примеры каждого из них уже произошли: сравните коррекцию абзаца, использованную в уроке чисел 3 чтобы показать, что простые числа образуют бесконечное множество с использованием доказательства в два столбца в Числах Урок 12, чтобы получить квадратичная формула. Традиционно (с 1900) Геометрия использовала доказательство в два столбца с левым столбцом, содержащим утверждение и правый столбец, содержащий соответствующее обоснование. Это то, с чем вы должны ознакомиться. Доказательства также могут быть прямыми или косвенными как описано в Числах, урок 5. Они также могут быть основаны на индуктивных или дедуктивных рассуждениях .
Правила построения, черчения и черчения
Древние греки установили несколько простых правил геометрического построения.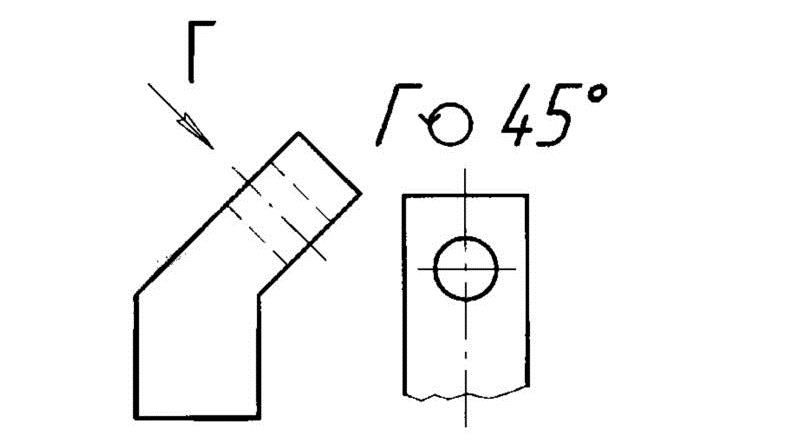 которые привели к некоторым интересным математическим разработкам в течение следующего
несколько тысяч лет, как обсуждалось ранее в
Числа Урок 14.
Таким образом, слово построить означает, что вы должны следовать этим правилам, которые
ограничивать ваши методы значительно. Конкретно,
вы можете использовать только линейку без маркировки и компас .
Эти три правила заключаются в следующем.
которые привели к некоторым интересным математическим разработкам в течение следующего
несколько тысяч лет, как обсуждалось ранее в
Числа Урок 14.
Таким образом, слово построить означает, что вы должны следовать этим правилам, которые
ограничивать ваши методы значительно. Конкретно,
вы можете использовать только линейку без маркировки и компас .
Эти три правила заключаются в следующем.- Правило начисления баллов: Балл должен быть либо задан, либо пересечение уже построенных фигур. Их можно назвать юридическими точками .
- Правило линейки: Линейка может быть использована для рисования линия через юридическую точку A и B .
- Правило компаса: Компас можно использовать для рисования дуги, содержащей второй юридический пункт B . Как правило, это означает, что компас можно поднять, сохраняя тот же радиус.
 В таких случаях вы также можете использовать 9линейка 0024 и транспортир .
Наконец, бывают случаи, когда вас могут попросить сделать набросок .
геометрическая фигура. В таких случаях не требуется использовать
линейка, чтобы убедиться, что ваши линии прямые или
транспортир, чтобы убедиться, что ваши углы правильно измерены.
В таких случаях вы также можете использовать 9линейка 0024 и транспортир .
Наконец, бывают случаи, когда вас могут попросить сделать набросок .
геометрическая фигура. В таких случаях не требуется использовать
линейка, чтобы убедиться, что ваши линии прямые или
транспортир, чтобы убедиться, что ваши углы правильно измерены.Следующая базовая конструкция алгоритмов должна быть освоил. Другие будут добавлены позже.
- Биссектриса данного отрезка.
- Биссектриса сегмента, обеспечивающая доступ только с одной стороны.
- Правильный (равносторонний) треугольник.
- Правильный шестигранник.
- Биссектриса угла.
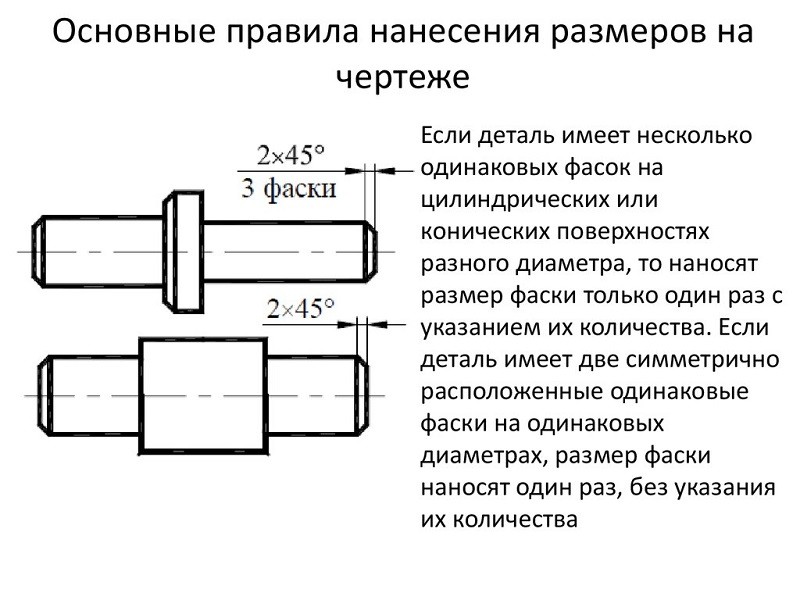 Однако получается очень занятая диаграмма.)
Соедините эти две точки пересечения.
Эти две точки явно равноудалены от обеих конечных точек.
как и все точки на линии, соединяющей их.
Однако получается очень занятая диаграмма.)
Соедините эти две точки пересечения.
Эти две точки явно равноудалены от обеих конечных точек.
как и все точки на линии, соединяющей их.Если сегмент расположен у края бумаги, то только одна точка в каждый момент времени может быть определена любым заданным радиусом. Таким образом, вы должны сбросить радиус компаса, чтобы найти вторую точку на той же стороне линии.
Чтобы построить равносторонний треугольник нарисуйте отрезок
и отметьте нужную длину.
Установите компас на эту длину, затем нарисуйте дугу с каждого конца
заданный отрезок так, чтобы они пересекались в одной точке с одной стороны.
(Опять же, если есть сомнения, можно использовать полные круги.)
Нарисуйте сегменты, соединяющие каждую конечную точку с пересечением этих
сегменты. Ясно, что все три стороны имеют одинаковую длину, треугольник
равносторонний, а так как треугольник равнобедренный по трем направлениям,
по теореме сравнения основных углов
(еще впереди) он также равноугольный.
Есть два основных способа построить правильный шестиугольник . В первом методе используется круг с радиусом желаемого длина шестигранника. Выберите точку на окружности, затем отметьте расстояние одного радиуса от вашего компаса. По мере продвижения вокруг цикла вы сделаете ровно шесть равных делений. Соедините их, чтобы завершить свой шестиугольник. Второй метод использует тот факт, что правильный шестиугольник можно триангулировать на шесть равносторонних треугольников. Постройте равносторонний треугольник, как описано выше. Нарисуйте круг с центром в одной вершине и действуйте, как описано выше.
Чтобы построить биссектрисы угла , установите компас почти на любое произвольное
но удобное расстояние. Поместите острие компаса на угол
вершина. Отметьте вспомогательные точки на каждом из лучей угла с помощью компаса.
на том же расстоянии от вершины. От каждого из этих двух вспомогательных
точки рисуют еще одну дугу внутри угла. (Новое расстояние
может быть выбран для этой пары отдельно от расстояния за пределами дуги,
но это необязательно. ) Точка пересечения, образованная дугой
из каждой вспомогательной точки лежат на прямой, образующей биссектрису угла.
Соедините их и продлите линию, чтобы завершить строительство.
) Точка пересечения, образованная дугой
из каждой вспомогательной точки лежат на прямой, образующей биссектрису угла.
Соедините их и продлите линию, чтобы завершить строительство.
Лабиринты и лабиринты
По следующей ссылке есть лабиринт и бесплатный загружаемый апплет для рисования. идеальных лабиринта : http://www.ericharshbarger.org/java. Совершенные лабиринты не только решаемы , но хорошо связаны и не содержат замкнутых циклов . Лабиринты и лабиринты имеют долгую историю, вероятно, возникло из оборонительных работ против врага. Позже они превратились в магические устройства против злых духов. Лабиринты часто содержат тупики и технически отличается от лабиринтов. В греческой мифологии, Минотавр был заточен в знаменитом критском лабиринте. Лабиринты живых изгородей или кукурузы (кукурузы) все еще распространены в таких садах, как Версаль, Хэмптон-Корт в Лондоне или в Айове. Возможно, в следующем году мы сможем совершить местную экскурсию в: Кукурузный лабиринт «Яблочный домик Уика» или Барбот Фермы. Лабиринт, имеющий только один вход и один выход, можно пройти, поместив
одну руку к любой стене и держите ее там, пока вы пересекаете лабиринт.
Обычно это не самое короткое решение, но выход всегда можно найти.
быть достигнуто таким образом. Чтобы это работало в лабиринте, должно быть
нет замкнутых циклов. Если у него нет замкнутых петель, это просто подключен в противном случае это многосвязных . Лабиринты также используются для проверки
обучающее поведение, особенно у мышей.
Лабиринт, имеющий только один вход и один выход, можно пройти, поместив
одну руку к любой стене и держите ее там, пока вы пересекаете лабиринт.
Обычно это не самое короткое решение, но выход всегда можно найти.
быть достигнуто таким образом. Чтобы это работало в лабиринте, должно быть
нет замкнутых циклов. Если у него нет замкнутых петель, это просто подключен в противном случае это многосвязных . Лабиринты также используются для проверки
обучающее поведение, особенно у мышей.Ниже/на следующей странице находится лабиринт из вашего домашнего задания.
Для домашнего задания 3.7.
| ЗАДНЯЯ ЧАСТЬ | ДОМАШНЕЕ ЗАДАНИЕ | ДЕЯТЕЛЬНОСТЬ | ПРОДОЛЖИТЬ |
|---|
- электронная почта: [email protected]
- голос/почта: 269 471-6629/ BCM&S Smith Hall 106; Университет Эндрюса; Берриен Спрингс,
- аудитория: 269 471-6646; Smith Hall 100/ ФАКС: 269 471-3713; МИ, 49104-0140
- домашний: 269 473-2572; 610 Н.
 Главная улица;
Берриен Спрингс, Мичиган 49103-1013
Главная улица;
Берриен Спрингс, Мичиган 49103-1013 - URL-адрес: http://www.andrews.edu/~calkins/math/webtexts/geom03.htm
- Copyright © 20002005, Кит Г. Калкинс. Пересмотрено 6 ноября 2005 г. или позднее.
ЧЕРТЕЖИ КОНСТРУКЦИОННОЙ СТАЛИ
КОНСТРУКЦИОННЫЕ ФОРМЫ И ЭЛЕМЕНТЫ
Различные конструкционные элементы используются для изготовления самых разных форм и размеров поперечного сечения. Многие формы показаны на рис. 7-1. Эти символы составлены из части 4 военного стандарта 18B (MIL-STD-18B) и информации Американского общества инженеров-строителей (ASCE). В следующих параграфах объясняются общие конструктивные формы, используемые в строительных материалах, и общие конструктивные элементы, изготовленные в этих формах.
Профили
Три наиболее распространенных типа элементов конструкции: W-образный (широкий фланец), S-образный (американский стандарт двутавровой балки) и C-образный (американский стандартный швеллер).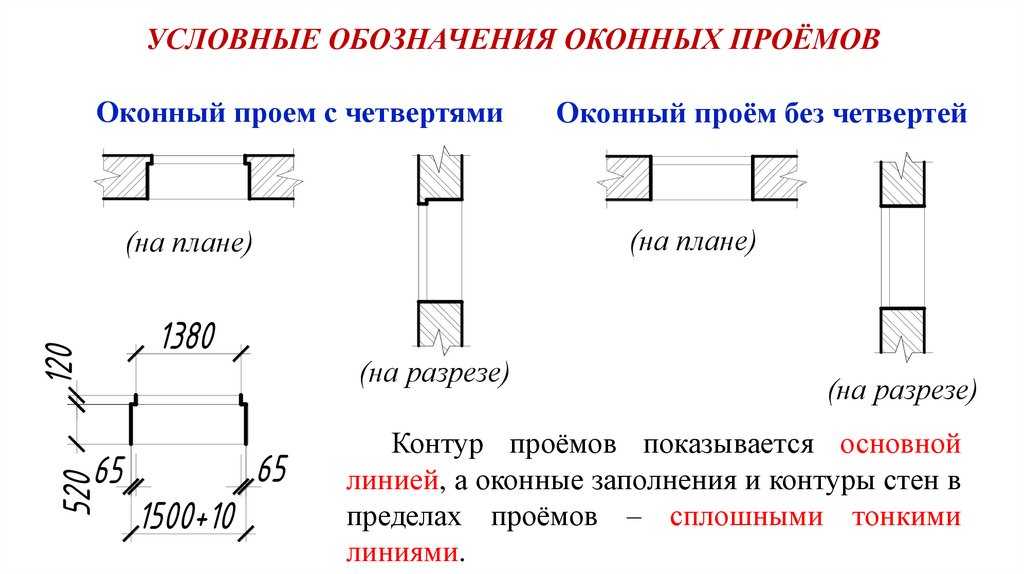 Эти три типа идентифицируются по номинальной глубине в дюймах вдоль стенки и весу на фут длины в фунтах. Например, W 12 x 27 указывает на W-образную форму (широкий фланец) со стенкой глубиной 12 дюймов и весом 27 фунтов на погонный фут.
Эти три типа идентифицируются по номинальной глубине в дюймах вдоль стенки и весу на фут длины в фунтах. Например, W 12 x 27 указывает на W-образную форму (широкий фланец) со стенкой глубиной 12 дюймов и весом 27 фунтов на погонный фут.
Виды поперечного сечения W-, S- и C-форм проиллюстрированы на Рисунке 7-2. Отличие W-образной формы от S-образной заключается в конструкции внутренних поверхностей фланца. W-образная форма имеет параллельные внутренние и внешние поверхности фланцев с постоянной толщиной, а S-образная форма имеет наклон приблизительно 17 градусов на внутренних поверхностях фланцев. С-образная форма похожа на S-образную тем, что ее внутренняя поверхность фланца также наклонена примерно на 17 градусов.
W-образная форма
W-образная форма представляет собой конструктивный элемент, поперечное сечение которого образует букву H, и является наиболее широко используемым конструктивным элементом. Он устроен так, что его полки обеспечивают прочность в горизонтальной плоскости, а стенка придает прочность в вертикальной плоскости. W-образные формы используются в качестве балок, колонн и элементов ферм, а также в других несущих конструкциях.
W-образные формы используются в качестве балок, колонн и элементов ферм, а также в других несущих конструкциях.
Несущая свая
Несущая свая (HP-форма) почти идентична W-образной. Единственное отличие состоит в том, что толщина полки и толщина стенки несущей сваи равны, тогда как W-образная форма имеет разную толщину стенки и полки.
S-образная форма
S-образная форма (двутавровая балка американского стандарта) отличается тем, что ее поперечное сечение имеет форму буквы I. S-образные формы используются реже, чем W-образные, поскольку S-образные формы обладают меньшей прочностью и менее адаптируемы, чем W-образные.
С-образная форма
С-образная форма (швеллер американского стандарта) имеет поперечное сечение, несколько похожее на букву С. Это особенно полезно в местах, где требуется одна плоская поверхность без выступающих фланцев с одной стороны. С-образная форма не очень эффективна для балки или колонны, когда используется отдельно. Однако эффективные сборные элементы могут быть изготовлены из швеллеров, собранных вместе с другими конструктивными формами и соединенных заклепками или сварными швами.
Однако эффективные сборные элементы могут быть изготовлены из швеллеров, собранных вместе с другими конструктивными формами и соединенных заклепками или сварными швами.
Каналы
Поперечное сечение канала похоже на квадратную букву С. Каналы идентифицируются по их номинальной глубине и весу на фут. Например, обозначение канала C9 x 13,4 по американскому стандарту на рис. 7-1 показывает номинальную глубину 9 дюймов и вес 13,4 фунта на погонный фут. Швеллеры в основном используются в местах, где одна плоская поверхность без выступающих фланцев на стороне требуется для. Однако канал не очень эффективен в качестве луча или столбца, когда используется отдельно. Но каналы могут быть собраны вместе с другими конструктивными формами и соединены заклепками или сваркой, чтобы сформировать эффективные составные элементы.
Уголки
Угол (рис. 7-3) представляет собой конструктивную форму, поперечное сечение которой напоминает букву L. Обычно используются два типа: равнополочный угол и неравнополочный угол. Угол определяется размером и толщиной его ножек, например, угол 6 дюймов на 4 дюйма на 1/2 дюйма. Размер ног должен быть получен путем измерения по внешней стороне задней части ног. Когда угол имеет неравные стороны, сначала указывается размер более широкой стороны, как на Рисунке 7-3 — Углы. пример только что привел. Третье измерение относится к толщине ножек, которые всегда имеют одинаковую толщину. Уголки могут использоваться в комбинации из двух или четырех элементов для формирования основных элементов. Один угол также может использоваться для соединения основных частей вместе.
Угол определяется размером и толщиной его ножек, например, угол 6 дюймов на 4 дюйма на 1/2 дюйма. Размер ног должен быть получен путем измерения по внешней стороне задней части ног. Когда угол имеет неравные стороны, сначала указывается размер более широкой стороны, как на Рисунке 7-3 — Углы. пример только что привел. Третье измерение относится к толщине ножек, которые всегда имеют одинаковую толщину. Уголки могут использоваться в комбинации из двух или четырех элементов для формирования основных элементов. Один угол также может использоваться для соединения основных частей вместе.
Пластины
Как правило, основное, что нужно помнить о пластинах, это то, что они имеют ширину более 8 дюймов и толщину 1/4 дюйма или более. Пластины обычно используются в качестве соединений между другими конструктивными элементами или в качестве составных частей сборных конструктивных элементов. Пластины, нарезанные по определенным размерам, могут иметь ширину от 8 дюймов до 120 дюймов и более и различную толщину. Края этих листов могут быть обрезаны ножницами (листы со сдвигом) или прокатаны под прямым углом (листы универсального проката).
Края этих листов могут быть обрезаны ножницами (листы со сдвигом) или прокатаны под прямым углом (листы универсального проката).
Часто пластины обозначаются по их толщине и ширине в дюймах, например пластины размером 1/2 дюйма x 24 дюйма. Длина во всех случаях указывается в дюймах. Обратите внимание на рис. 7-4, что 1 кубический фут стали весит 490 фунтов. Этот вес, разделенный на 12, равняется 40,8, что является весом (в фунтах) стальной пластины площадью 1 квадратный фут и толщиной 1 дюйм. Дробная часть обычно отбрасывается, а 1-дюймовая тарелка называется 40-фунтовой тарелкой. На практике вы можете услышать, что плита упоминается по ее приблизительному весу на квадратный фут для определенной толщины. Примером может служить 20-фунтовая тарелка, что означает 1/2-дюймовую тарелку.
Обозначения, обычно используемые для плоского проката, были установлены Американским институтом чугуна и стали (AISI). Плоская сталь обозначается как пруток, полоса, лист или плита в зависимости от толщины материала, ширины материала и (в некоторой степени) процесса прокатки, которому он подвергался.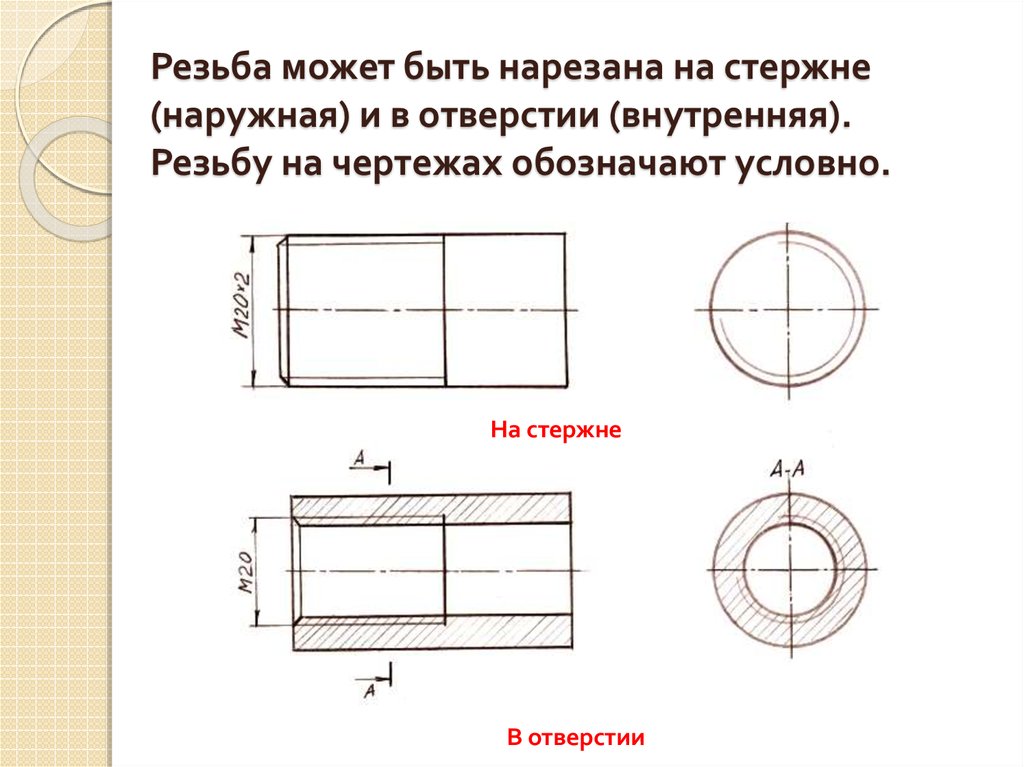
Тройники
Строительный тройник изготавливается путем разрезания стандартной двутавровой или двутавровой балки по центру ее стенки с образованием двух Т-образных профилей из каждой балки. При определении размеров перед символом структурного тройника ставятся буквы ST. Например, обозначение ST 5 WF 10,5 означает, что тройник имеет номинальную глубину 5 дюймов, широкий фланец и весит 10,5 фунтов на погонный фут. Катаный тройник представляет собой изготовленную форму. При обозначении размеров перед символом катаного тройника ставится буква Т. Размер Т 4 х 3 х 9.2 означает, что прокатанный Т имеет 4-дюймовый фланец, номинальную глубину 3 дюйма и вес 9,2 фунта на погонный фут.
Zee
Эти формы различаются по глубине, ширине полки и весу на погонный фут. Следовательно, Z 6 x 3 1/2 x 15,7 означает, что зи имеет глубину 6 дюймов, фланец 3 1/2 дюйма и весит 15,7 фунтов на погонный фут.
Плоский стержень
Структурная форма, называемая стержнем, имеет ширину 8 дюймов или меньше и толщину более 3/16 дюйма. Кромки прутков обычно завальцованы под прямым углом, как универсальные прокатные плиты. Размеры выражаются так же, как и для пластин, например, бар 6 дюймов на 1/2 дюйма. Стержни доступны в различных формах поперечного сечения – круглые, шестиугольные, восьмиугольные, квадратные и плоские. Четыре различных формы показаны на рис. 7-5. Как квадраты, так и круглые обычно используются в качестве элементов жесткости легких конструкций. Их размеры в дюймах относятся к стороне квадрата или диаметру круга.
Кромки прутков обычно завальцованы под прямым углом, как универсальные прокатные плиты. Размеры выражаются так же, как и для пластин, например, бар 6 дюймов на 1/2 дюйма. Стержни доступны в различных формах поперечного сечения – круглые, шестиугольные, восьмиугольные, квадратные и плоские. Четыре различных формы показаны на рис. 7-5. Как квадраты, так и круглые обычно используются в качестве элементов жесткости легких конструкций. Их размеры в дюймах относятся к стороне квадрата или диаметру круга.
Колонны
Обычно для колонн используются элементы с широкими полками, как можно ближе к квадратному в поперечном сечении, но иногда используются трубы большого диаметра, даже если трубные колонны могут создавать трудности при соединении колонн при креплении других элементов (Рисунок 7). -6). Колонны также могут быть изготовлены путем сварки или соединения болтами ряда других профилей проката, обычно уголков и пластин (рис. 7-7).
Балки
Балки — это основные горизонтальные элементы конструкции стального каркаса.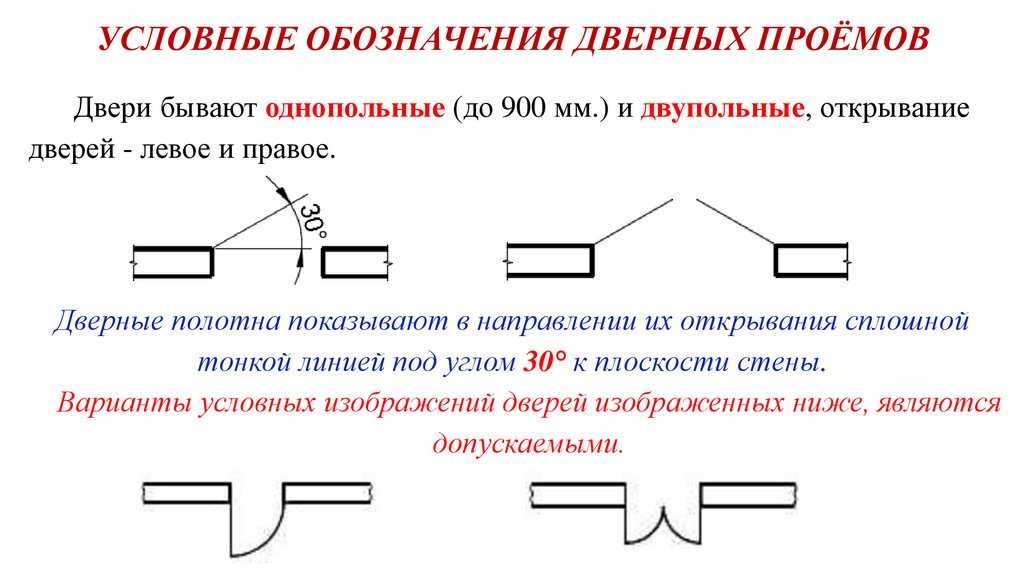 Они соединяются от колонны к колонне и обычно соединяются сверху колонн с помощью накладок (подшипники) (рис. 7-8). Альтернативным методом является сидячее соединение (рис. 7-9). Балка крепится к полке колонны с помощью уголков, при этом одна нога проходит вдоль полки балки, а другая напротив колонны. Функция балок заключается в поддержке балок межэтажного перекрытия.
Они соединяются от колонны к колонне и обычно соединяются сверху колонн с помощью накладок (подшипники) (рис. 7-8). Альтернативным методом является сидячее соединение (рис. 7-9). Балка крепится к полке колонны с помощью уголков, при этом одна нога проходит вдоль полки балки, а другая напротив колонны. Функция балок заключается в поддержке балок межэтажного перекрытия.
Элементы
Основными частями конструкции являются несущие элементы. Они поддерживают и передают нагрузки на конструкцию, оставаясь при этом равными друг другу. Места, где элементы соединяются с другими элементами, называются соединениями. Общая сумма нагрузок, воспринимаемых элементами конструкции в конкретный момент времени, равна общей статической нагрузке плюс общая временная нагрузка.
Общая статическая нагрузка — это общий вес конструкции, который постепенно увеличивается по мере подъема конструкции и остается постоянным после ее завершения. Общая динамическая нагрузка — это общий вес подвижных объектов, таких как люди, мебель и движение по мосту, которые конструкция поддерживает в определенный момент.
Базовая система – стойка и балка (каркасная рама) и пространственные рамы.
2. Преимущества конструкции со стальным каркасом:
1. Можно строить очень высокие и широкие (самые высокие здания в мире)
2. Легкий и прочный (намного легче и прочнее, чем бетон)
3. Сборный – каркас быстро собирается
4. Точный и предсказуемость (отличный контроль качества)
3. Недостатки конструкции со стальным каркасом:
1. Сталь — дорогой материал (гораздо дороже кирпичной кладки или бетона)
2. Каркасы неустойчивы
3. Требует противопожарной защиты
4. Требует отдельной «обшивки» (стены и полы)
4. Методы стабилизации зданий со стальным каркасом:
1. Жесткое ядро - обычно достигается за счет внутренней кладки (или бетона) лестничных башен и лифтовых шахт, создающих вертикальное жесткое ядро, противодействующее деформациям и кручению здания под действием внешних боковых сил.
2. Диагональные распорки — добавление диагональных распорок «X» или «K», которые противостоят боковым нагрузкам.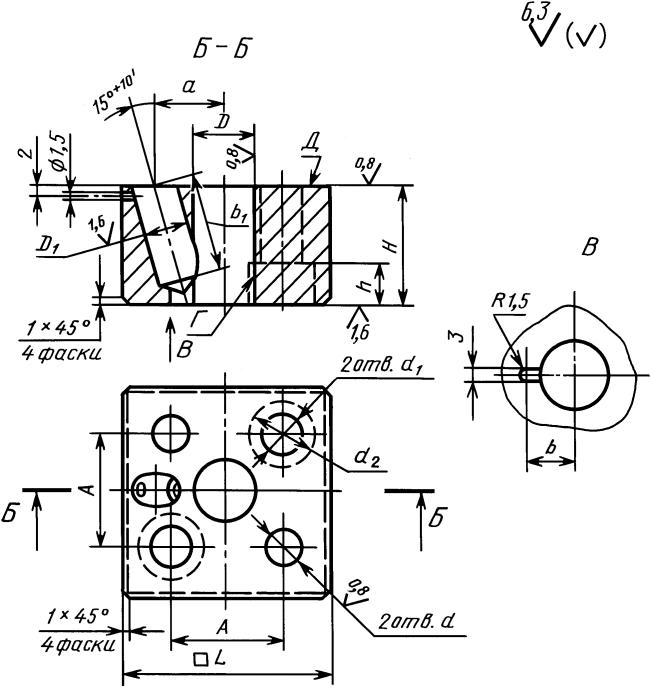 Проблемы – могут мешать внешние окна.
Проблемы – могут мешать внешние окна.
3. Устойчивые к моменту соединения балки с колонной. Обычно выполняются путем изготовления дополнительных соединительных уголков, сварных швов и болтов, которые значительно повышают жесткость соединения. Проблемы – крайне трудоемкие и дорогие.
4. Стены жесткости – Наружные (или внутренние) стены, построенные из кирпичной кладки или бетона, которые действуют как вертикальная консольная балка, воспринимающая боковые нагрузки. Проблемы – могут мешать наружные окна, трудоемкость, тяжесть.
5. Основные профили из конструкционной стали (горячекатаные):
Как правило, конструкционная сталь изготавливается методом горячей прокатки под несколькими обозначениями ASTM, наиболее распространенным из которых является A36. Эта сталь имеет минимальный предел текучести 36 тысяч фунтов на квадратный дюйм и минимальное предельное (разрушающее) напряжение 58 тысяч фунтов на квадратный дюйм. Доступны многие другие марки, с пределом текучести A572 – 50 KSI в качестве выбора для более высокой прочности. Новая марка стали A992 недавно заменила A572 и A36 (для профилей W) в качестве стандартной марки стали. Как и A572, он также имеет предел текучести 50 KSI.
Новая марка стали A992 недавно заменила A572 и A36 (для профилей W) в качестве стандартной марки стали. Как и A572, он также имеет предел текучести 50 KSI.
1. Широкая полка — типичная «двутавровая балка», используемая в строительстве. Пример — W18x35, где «W» = широкая полка, 18 = номинальная глубина элемента в дюймах и 35 = вес балки в фунтах на погонный фут. Используется для балок, колонн, свай, распорок и других тяжелых применений.
2. Углы – равнополочные или неравнополочные. Пример — L4 x 3 x 1/4, где 4 и 3 — фактические размеры полки в дюймах, а 1/4 = толщина уголка в дюймах. Используется для перемычек, раскосов, составных балок и колонн, вторичного каркаса и других легких применений.
3. Стальные швеллеры — эти элементы в форме буквы «С» используются для балок, сборных колонн, распорок, вторичного каркаса и других применений с легкими и средними нагрузками. Примером канала является C10x30, где «C» обозначает канал, 10 — фактическая высота канала в дюймах, а 30 = фунты на погонный фут.
4. Стальная труба. Круглая труба чаще всего используется для колонн. Выпускается в трех категориях в зависимости от диаметра и толщины стенки: «стандартный вес», «сверхпрочный» и «двойной сверхпрочный». Двойная сверхпрочная труба является самой прочной, потому что у нее самые толстые стенки. Пример — труба стандартного веса диаметром 4 дюйма
5. Трубчатая сталь – эти квадратные или прямоугольные сечения чаще всего используются в качестве колонн, но также могут использоваться в качестве балок, распорок или других применений. Типичным примером является TS6x4x1/4, где TS = трубная сталь, 6 и 4 — фактическая ширина и глубина в дюймах, а 1/4 — толщина стенки в дюймах.
С 2003 года трубная сталь теперь называется Американским институтом стальных конструкций «полым конструкционным сечением» (HSS). Типичное обозначение HSS6x4x1/4.
6. Пластины – плоские куски стали, нарезанные по размеру. Обычно в диапазоне от 1/8 дюйма до 6 дюймов. Используется в качестве опорных плит колонн, сборных балок и колонн (т.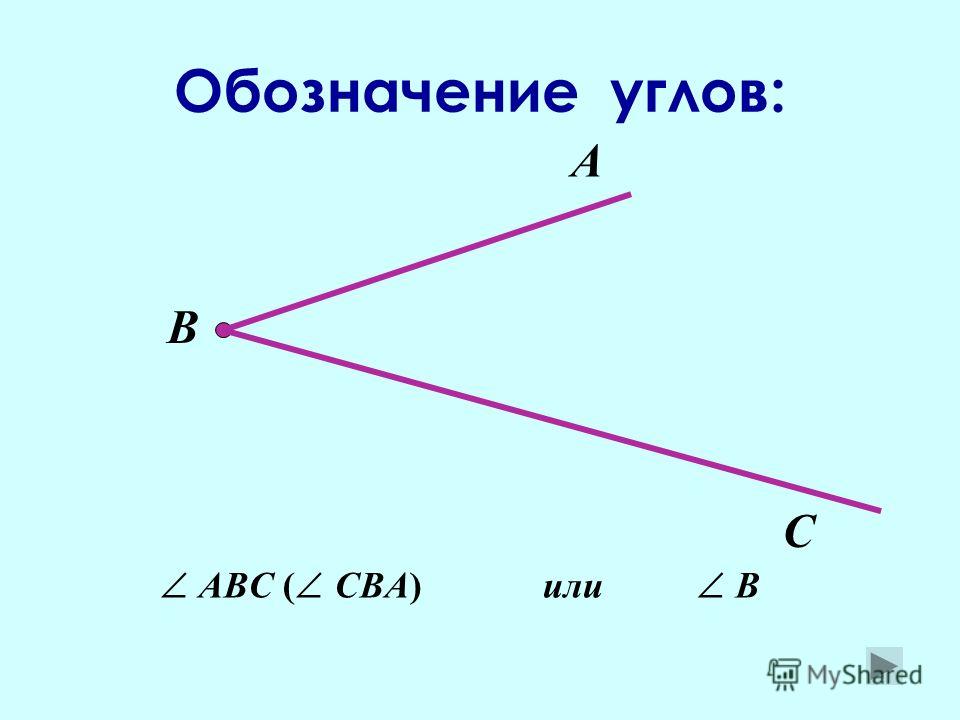 е. пластинчатых ферм), соединительных деталей (т. е. косынок, сварных пластин и т. д.) и любого другого применения, где требуются детали определенного размера. Пример – PL 6x4x3/8, где 6 и 4 – длина и ширина листа в дюймах, а 3/8 – толщина листа в дюймах.
е. пластинчатых ферм), соединительных деталей (т. е. косынок, сварных пластин и т. д.) и любого другого применения, где требуются детали определенного размера. Пример – PL 6x4x3/8, где 6 и 4 – длина и ширина листа в дюймах, а 3/8 – толщина листа в дюймах.
7. Вырезанные секции. Обычно это секции с широкими полками, которые разрезаются пополам, образуя Т-образную секцию. Используется для перемычек, балок, раскосов и колонн. Пример – WT7x19 представляет собой секцию, вырезанную из широкой полки W14x38.
5. Соединения:
6. Заклепки – Обычно больше не используются по таким причинам, как низкая прочность, безопасность и плохой контроль качества.
1. Болты – бывают двух видов – из углеродистой стали и высокопрочные. Болты из углеродистой стали получают свою прочность за счет сдвига (или растяжения) только вдоль стержня болта. Наиболее распространенное обозначение ASTM для болтов из углеродистой стали, используемых в конструкциях, – A307.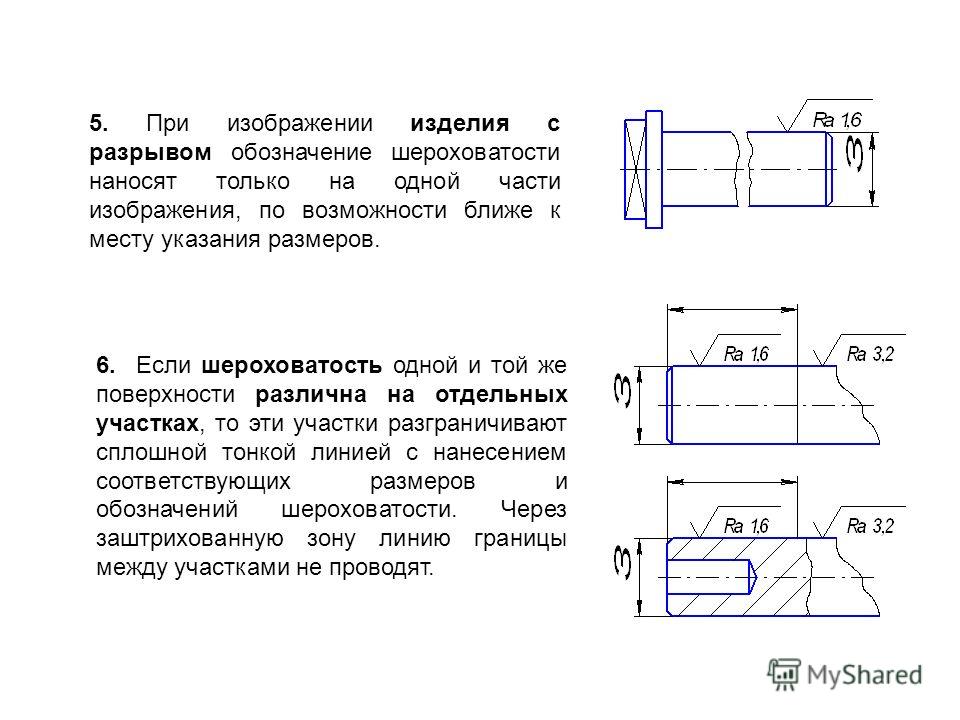 Эти болты не могут нести ту же нагрузку, что и высокопрочные болты, и используются для легких условий эксплуатации, таких как анкерные болты. Высокопрочные болты получают свою прочность не только за счет сдвига и растяжения вдоль вала, но и за счет сил трения, возникающих при натяжении гайки до заданного уровня. Самый распространенный ASTM
Эти болты не могут нести ту же нагрузку, что и высокопрочные болты, и используются для легких условий эксплуатации, таких как анкерные болты. Высокопрочные болты получают свою прочность не только за счет сдвига и растяжения вдоль вала, но и за счет сил трения, возникающих при натяжении гайки до заданного уровня. Самый распространенный ASTM
2. Сварка. Сварка осуществляется путем механического соединения стали с помощью нагревательных электродов в расплавленном состоянии, которое образует одно целое из двух. Создает чрезвычайно жесткие соединения. Наиболее распространенным типом сварки, используемым для строительных конструкций, является «угловой» шов, который соединяет детали под прямым углом. Обычно соединительные уголки к балкам и колоннам приваривают в цеху, а затем скрепляют их болтами в полевых условиях на стройплощадке.
7. Стальной настил:
Стальной настил относится к одному из нескольких основных типов. Весь настил холоднокатаный и продается толщиной от 16 (самая тяжелая) до 28 (самая легкая).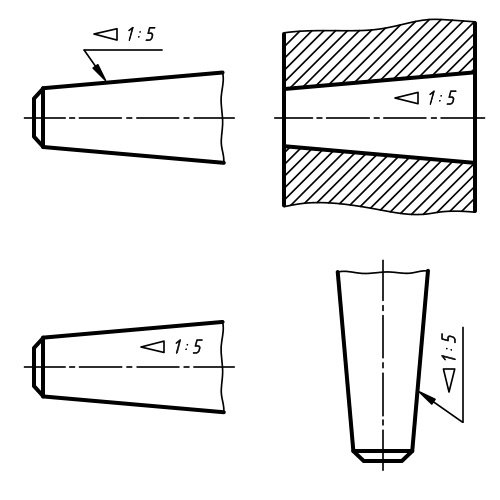
1. Настил крыши – обычно доступен высотой 1½ дюйма и 3 дюйма и толщиной от 16 до 22 калибров. Настил крыши характеризуется тем, что верхняя канавка намного шире, чем нижняя, что обеспечивает максимально возможную плоскую поверхность для несущих ненесущих компонентов здания, таких как жесткая изоляция. Ширина нижней канавки варьируется, и доступны различные профили, такие как «узкое ребро», «промежуточное ребро» и «широкое ребро».
2. Настил пола (некомпозитный) — используется для полов, этот тип настила имеет примерно одинаковую длину верхних и нижних канавок и действует как форма для бетона. Типичные доступные высоты: 9/16″, 1″, 1 5/16″, 1½”, 2″ и 3″. Бетон, уложенный на настил, обычно армируется сварной проволочной тканью.
3. Настил пола (композитный) — Подобно настилу пола из некомпозитного материала, этот настил обычно имеет дополнительные перфорации в настиле для «сцепления» с бетоном. Эта палуба действует как часть структурной системы со стальными балками.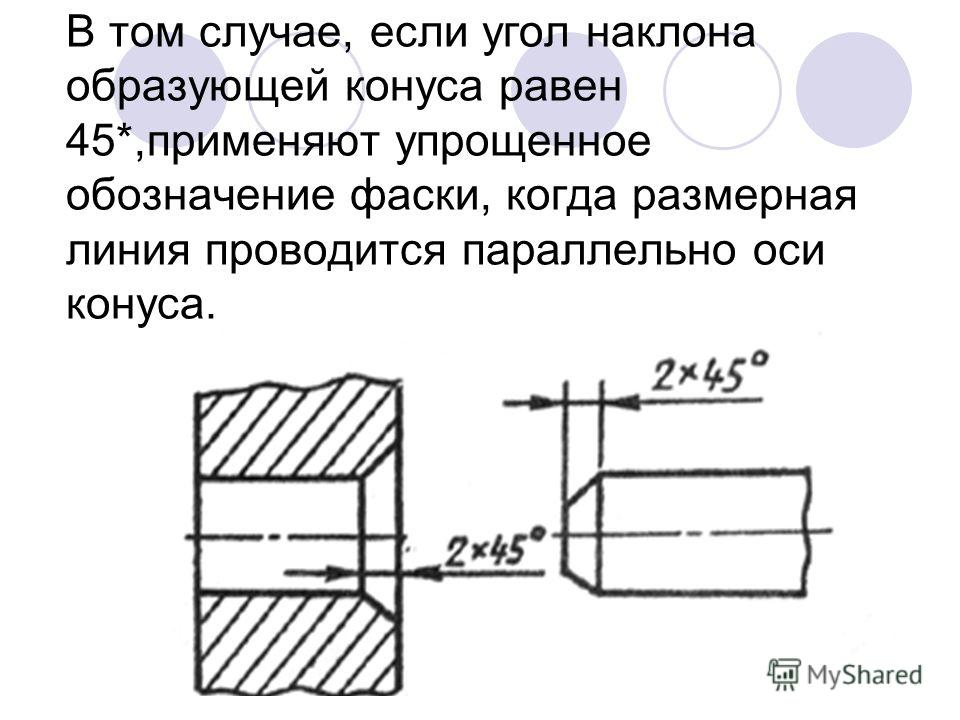 Настил размещается поверх стальной балки, а стальные «шпильки» привариваются через настил и к верхней полке балки. После того, как бетон уложен и отвержден, он захватывает срезные шпильки и взаимодействует со стальной балкой, значительно увеличивая несущую способность одной только стальной балки.
Настил размещается поверх стальной балки, а стальные «шпильки» привариваются через настил и к верхней полке балки. После того, как бетон уложен и отвержден, он захватывает срезные шпильки и взаимодействует со стальной балкой, значительно увеличивая несущую способность одной только стальной балки.
8. Стальные балки (стержневые балки):
Эти легкие фермы с открытой стенкой производятся различными компаниями (такими как Vulcraft), чтобы обеспечить максимально легкую альтернативу балкам. Они используются чаще всего для сборки крыши. Типичная стальная балка показана ниже:
9. Легкий стальной каркас:
Легкие стальные каркасы используются для каркаса стен, перекрытий, балок и перемычек — всего, для чего используются обычные деревянные каркасы. Строительные нормы и правила большинства штатов предписывают использовать негорючие конструкции для объектов определенного типа, а элементы деревянного каркаса использовать НЕЛЬЗЯ.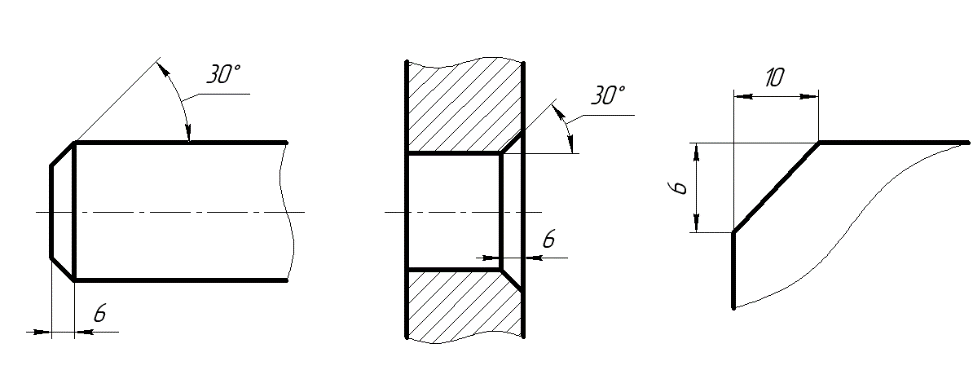 Эти легкие элементы представляют собой холоднокатаные (аналогичные стальному настилу) изделия из листового металла, которые доступны от различных производителей в виде элементов «С» в калибрах, обычно от 12 до 26 калибров. Они крепятся и собираются с помощью саморезов и точечной сварки.
Эти легкие элементы представляют собой холоднокатаные (аналогичные стальному настилу) изделия из листового металла, которые доступны от различных производителей в виде элементов «С» в калибрах, обычно от 12 до 26 калибров. Они крепятся и собираются с помощью саморезов и точечной сварки.
10. Противопожарная защита:
Все стальные конструкции должны быть защищены от огня в соответствии с государственными и местными строительными нормами. Хотя для фактического плавления стали требуется очень значительное количество тепла, она теряет большую часть своей прочности при температурах выше 7000 F. Обычно существуют две основные категории огнезащиты – термическая и абсорбционная.
1. Тепловая противопожарная защита – замедляет прохождение тепла через сталь. Используемые методы включают изоляцию и вспучивающуюся краску.
2. Абсорбционная противопожарная защита – поглощает тепло. Используемые методы включают покрытие стальных элементов бетоном, гипсом (напылением) и сложные методы, такие как заполненные жидкостью камеры (обычно оборачиваются вокруг колонн).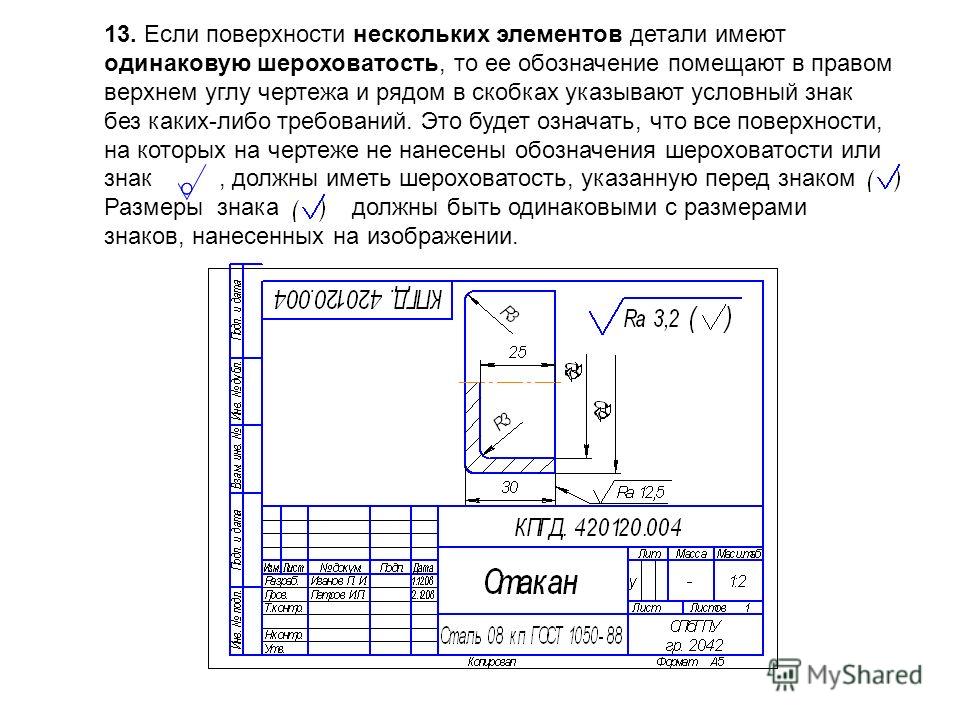
СВАРНЫЕ И КЛЕПНЫЕ СТАЛЬНЫЕ КОНСТРУКЦИИ
В следующих параграфах обсуждаются сварные и клепаные стальные конструкции и приводятся примеры обоих методов изготовления ферм.
Сварные стальные конструкции
Как правило, сварные соединения обрамляются или фиксируются точно так же, как и клепаные соединения, которые мы обсудим позже. Однако сварные соединения более гибкие. Отверстия, используемые для соединения деталей болтами или штифтами во время сварки, обычно просверливаются в производственной мастерской. Балки обычно не привариваются непосредственно к колоннам. Процедура обеспечивает жесткое соединение и приводит к сильному изгибу, который создает нагрузку на балку, которой должны сопротивляться как балка, так и сварной шов.
Обозначение сварки
Чертежи содержат специальные обозначения для указания места сварки, типа соединения, а также размера и количества наплавляемого металла в месте соединения. Американское общество сварщиков (AWS) стандартизировало их. Сварщик увидит их всякий раз, когда он или она будет выполнять сварочное задание из набора распечаток, поэтому вам необходимо ознакомиться со всеми элементами стандартного символа сварки, а также с расположением и значением основных символов сварки.
Американское общество сварщиков (AWS) стандартизировало их. Сварщик увидит их всякий раз, когда он или она будет выполнять сварочное задание из набора распечаток, поэтому вам необходимо ознакомиться со всеми элементами стандартного символа сварки, а также с расположением и значением основных символов сварки.
Стандартный символ сварки (рис. 7-15): контрольная линия + стрелка + хвост.
Базовая линия – это основа. На него наносятся символы сварки, размеры и другие данные. Стрелка соединяет контрольную линию с соединением или областью, подлежащей сварке. Направление стрелки не имеет отношения к значению опорной линии. Конец символа сварки используется только при необходимости для включения информации о процессе, спецификации или другой справочной информации.
Обозначения типов сварных швов
Обозначения сварных швов относятся к обозначениям для определенного типа сварного шва, такого как угловой шов, паз, стык, наплавка, пробка или паз.
Символ сварки (Рисунок 7-16) является лишь частью информации, необходимой для обозначения сварки. При использовании для распространения информации термин «символ сварки» относится к общему символу, который включает в себя все символы сварки, необходимые для указания требуемых сварных швов.
При использовании для распространения информации термин «символ сварки» относится к общему символу, который включает в себя все символы сварки, необходимые для указания требуемых сварных швов.
Наложение символа сварного шва на контрольную линию показано на рис. 7-17. Обратите внимание, что вертикальная сторона символа сварки показана слева от наклонной или изогнутой стороны символа. Независимо от того, относится ли символ к угловому, фасочному, J-образному или развальцовочному шву, вертикальная сторона всегда рисуется влево. Значение положения символа сварки на опорной линии показано на рис. 7-18.
Когда необходимо скосить только одну кромку соединения, необходимо показать, какой элемент должен быть скошен (Рисунок 7-19). Когда указан такой стык, стрелка символа сварки указывает с определенным разрывом на деталь, подлежащую скосу. Другие символы сварки могут быть добавлены к символу сварки по мере необходимости для передачи всей информации, необходимой для сварки.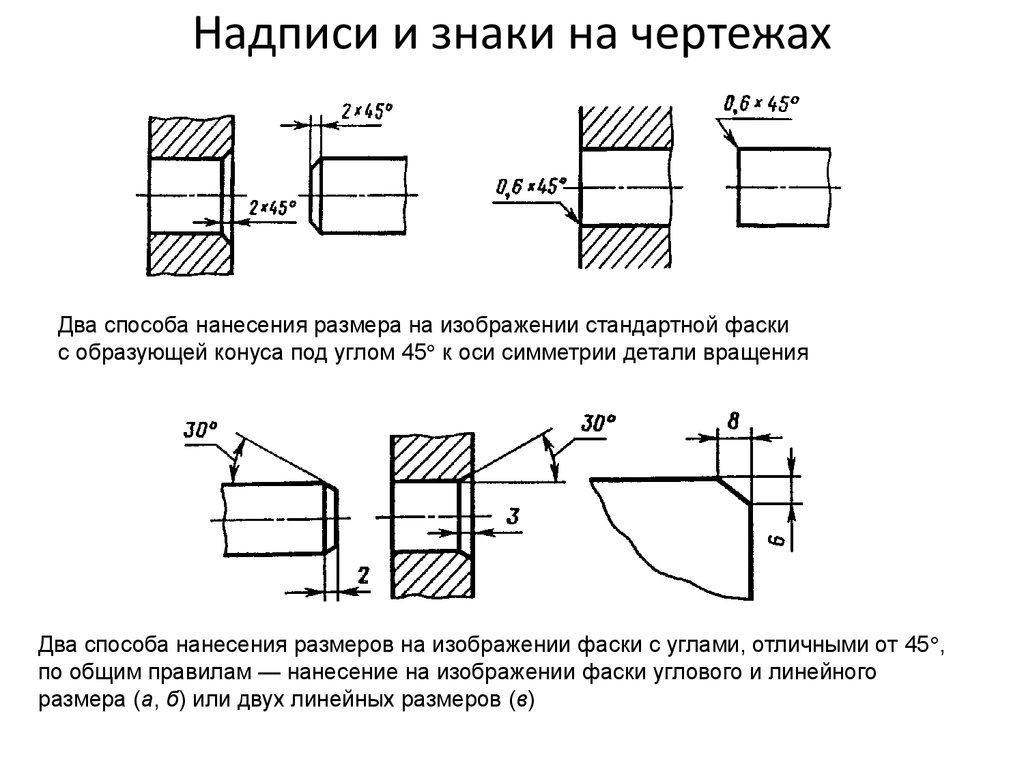
Однако, независимо от направления стрелки, вся информация, нанесенная на опорную линию символа сварки, читается слева направо. Список символов сварки показан на рис. 7-20.
Размер, длина, шаг (расстояние между центрами), угол разделки кромок и открытие корня сварного шва имеют определенные местоположения. Эти местоположения определяются стороной контрольной линии, на которой размещен символ сварки.
Дополнительный
Помимо основных символов сварки, символ сварки может включать дополнительные символы (Рисунок 7-22). Контурные символы показывают, как должно быть сформировано лицо; символы отделки указывают метод, используемый для формирования контура.
Символ отделки (если он используется) показывает метод отделки, C обозначает скалывание, M означает механическую обработку, а G обозначает шлифовку, а не степень отделки. Как символы контура и отделки применяются к символу сварки, показано на Рис. 7-23. Этот символ указывает на то, что сварной шов должен быть зачищен заподлицо. Также обратите внимание, что символы размещаются с той же стороны от базовой линии, что и символ сварного шва.
Также обратите внимание, что символы размещаются с той же стороны от базовой линии, что и символ сварного шва.
Другим дополнительным символом является символ сварки по всему периметру. Когда этот символ помещается на символ сварки, сварные швы должны продолжаться по всему стыку.
Еще один символ на Рисунке 7-22 — это символ монтажной сварки, черный флажок, указывающий на конец символа сварки. Для сварных швов, которые не могут быть выполнены в цеху из-за размера, транспортировки, конструктивных особенностей или по другим причинам, этот символ указывает сварщику выполнить сварку в полевых условиях, которая может выполняться «на месте» или на месте.
Сварные стальные фермы
Чертеж типичной сварной стальной фермы показан на рис. 7-24. Когда вы интерпретируете символы сварки, вы увидите, что большинство из них показывают, что конструкционные углы будут сварены угловым швом. Скругление будет иметь радиус 1/4 дюйма (толщину) с обеих сторон и будет проходить вдоль угла на протяжении 4 дюймов.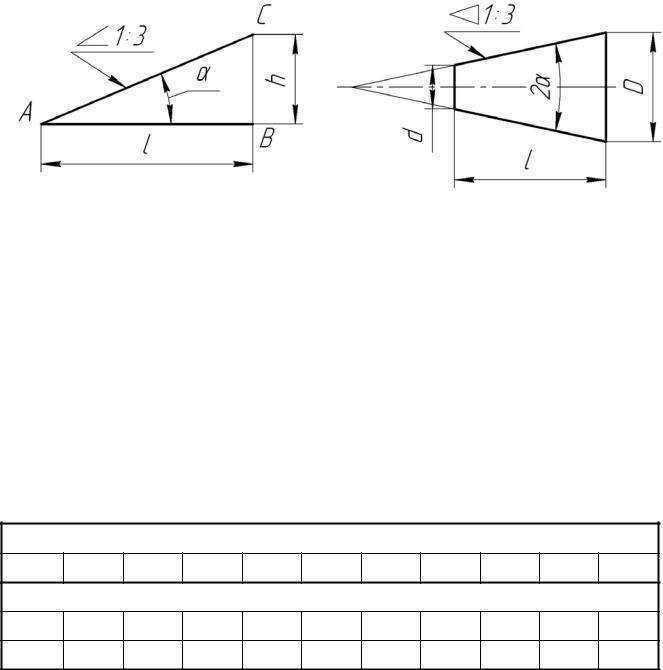
Сварные стальные фермы
Чертеж типичной сварной стальной фермы показан на рис. 7-24. Когда вы интерпретируете символы сварки, вы увидите, что большинство из них показывают, что конструкционные углы будут сварены угловым швом. Скругление будет иметь радиус 1/4 дюйма (толщину) с обеих сторон и будет проходить вдоль угла на протяжении 4 дюймов.
Стальные клепаные конструкции
Элементы стальных конструкций клепаются в цехе, где они изготавливаются, в объеме, допускаемом условиями отгрузки. Во время изготовления все отверстия для заклепок пробиваются или сверлятся независимо от того, должны ли заклепки забиваться в полевых условиях или в мастерской.
Посмотрите на производственный чертеж клепаной стальной фермы крыши на рис. 7-25. На первый взгляд он кажется загроможденным и трудночитаемым. Это вызвано множеством размеров и других соответствующих фактов, требуемых на чертеже, но вы можете прочитать его, как только поймете, что ищете, как мы объясним в следующих параграфах.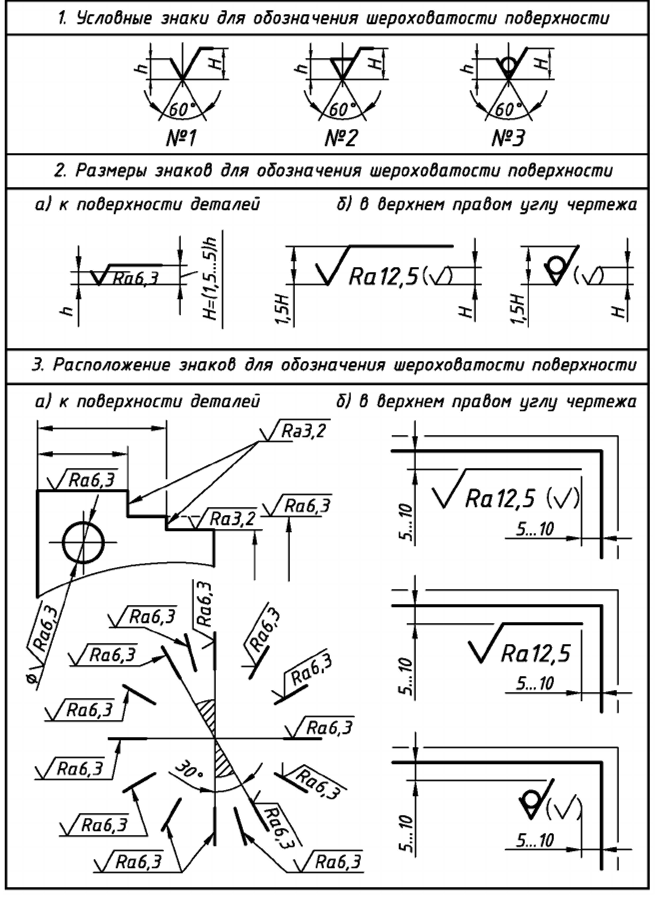
Верхний пояс состоит из двух углов, обозначенных спецификацией 2L 4 x 3 1/2 x 5/16 x 16´-5 1/2″. Это означает, что хорда составляет 4 дюйма на 3 1/2 дюйма на 5/16 дюйма толщиной и 16 футов 5 1/2 дюйма длиной.0076 Верхний пояс также имеет спецификацию IL 4 x 3 x 3/8 x 7(e). Это означает, что к нему прикреплено пять зажимных уголков, и каждый из них представляет собой угол размером 4 дюйма на 3 дюйма, толщиной 3/8 дюйма и длиной 7 дюймов.
Косынка (а) в левом нижнем углу вида имеет маркировку PL 8 x 3/8 x 1´-5 (а). Это означает, что его ширина составляет 8 дюймов, толщина — 3/8 дюйма, а длина — 1 фут 5 дюймов.
Нижний пояс состоит из двух уголков 2 1/2 дюйма на 2 дюйма на 5/16 дюйма на 10 футов 3 7/16 дюйма, которые соединены с косынками A и B, и еще двух уголков 2 1/2 дюймов на 2 дюйма на 1/4 дюйма на 10 футов 4 1/8 дюйма, которые соединяются с косынкой B и продолжаются до другой половины фермы. Еще два уголка соединены с косынками С и В на верхнем и нижнем поясах; они 2 1/2 дюйма на 2 дюйма на 1/4 дюйма на 2 фута 10 1/2 дюйма. Другой элемент между верхним и нижним поясами, соединенный с косынкой B и косынкой D, состоит из двух уголков 2 1/2 дюйма на 2 дюйма на 1/4 дюйма на 8 футов 5 дюймов.
Другой элемент между верхним и нижним поясами, соединенный с косынкой B и косынкой D, состоит из двух уголков 2 1/2 дюйма на 2 дюйма на 1/4 дюйма на 8 футов 5 дюймов.
Рисунок 7-27 — Размеры клепаной стальной фермы.
На Рис. 7-26 та же ферма показана только с названиями некоторых элементов и размерами косынок (A, C и D) между углами.
На рис. 7-27 та же ферма показана только с некоторыми необходимыми размерами, чтобы упростить чтение полного рабочего чертежа конструкции.
Большая часть заклепок будет забита в цехе, за исключением пяти заклепок в косынке прогона d и двух показанных заклепок, соединяющих центральную часть нижнего пояса, который соединяется с косынкой b. Эти семь заклепок будут вбиты на стройплощадке. Условные обозначения заклепок, забиваемых в цеху и в полевых условиях, показаны на рис. 7-28.
ЧЕРТЕЖИ СТАЛЬНЫХ КОНСТРУКЦИЙ
Чертежи, используемые для изготовления и монтажа стальных конструкций, обычно состоят из группы различных типов чертежей, таких как компоновочные, общие, производственные, монтажные и монтажные.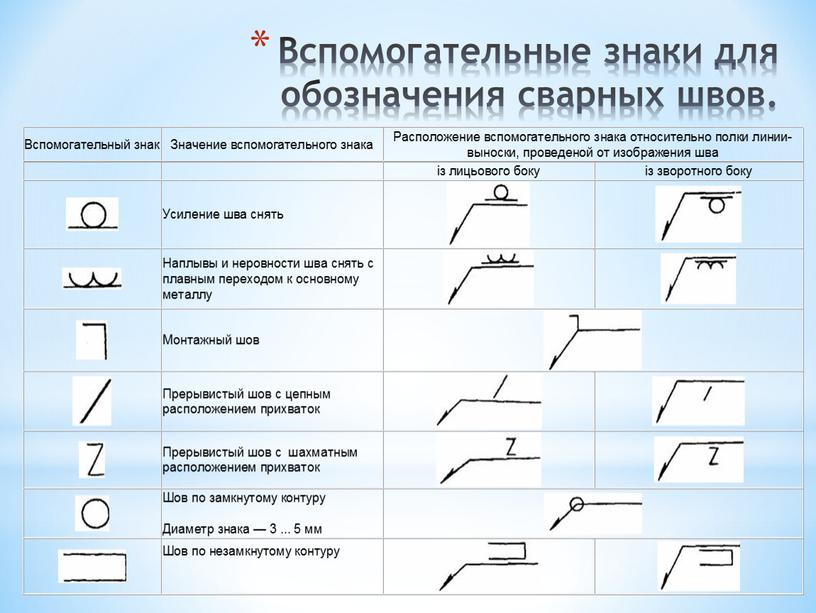 Эти чертежи описаны в следующих параграфах.
Эти чертежи описаны в следующих параграфах.
Компоновочные чертежи
Компоновочные чертежи также называются общими планами и чертежами профилей. Они предоставляют необходимую информацию о местоположении, выравнивании и высоте конструкции и ее основных частей относительно земли на площадке. Они также предоставляют другие важные сведения, такие как характер подстилающего грунта или расположение прилегающих сооружений и дорог. Эти чертежи дополняются инструкциями и информацией, известной как письменные спецификации.
Общие планы
Общие планы содержат информацию о размерах, материале и составе всех основных элементов конструкции, их взаимном расположении и способе соединения, а также крепления других частей конструкции. Количество поставляемых чертежей общего плана определяется такими факторами, как размер и характер сооружения, сложность операций. Общие планы состоят из видов в плане, фасадов и разрезов сооружения и его различных частей. Объем необходимой информации определяет количество и расположение секций и фасадов.
Производственные чертежи
Производственные чертежи или заводские чертежи содержат необходимую информацию о размере, форме, материале и положениях для соединений и креплений для каждого элемента. Эта информация достаточно подробна, чтобы можно было заказать материал для соответствующего элемента и изготовить его в магазине или на верфи. Составные части элементов показаны на производственном чертеже, а также размеры и монтажные метки.
Монтажные чертежи
Монтажные чертежи или монтажные схемы показывают расположение и положение различных элементов готовой конструкции. Они особенно полезны для персонала, выполняющего монтаж в полевых условиях. Например, на монтажных чертежах указан приблизительный вес тяжелых деталей, их количество и другие полезные данные.
Фальш-конструкция Чертежи
Термин фальш-конструкция относится к временным опорам из дерева или стали, необходимым при возведении сложных или важных конструкций.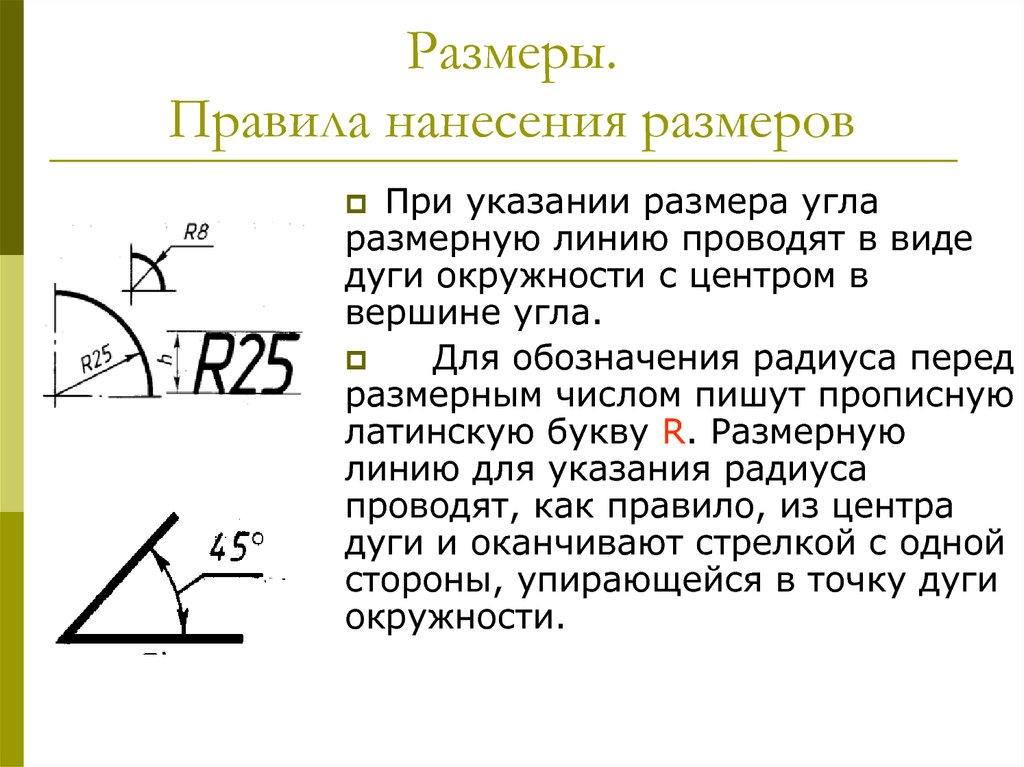 Когда требуется ложная работа в сложном масштабе, чертежи, аналогичные уже описанным общим и детальным чертежам, могут быть предоставлены для руководства строительством. Для простой фальшивой работы достаточно полевых зарисовок.
Когда требуется ложная работа в сложном масштабе, чертежи, аналогичные уже описанным общим и детальным чертежам, могут быть предоставлены для руководства строительством. Для простой фальшивой работы достаточно полевых зарисовок.
Уголки стальные равнополочные
Размеры и статические параметры уголков стальных равнополочных – британские единицы.
Рекламные ссылки
Свойства стальных уголков равнополочных в имперских единицах указаны ниже.
- Стальные углы – Равные ноги – метрические единицы
| Размер (в x in) | Размеры | Статические параметрии | Параметоры STATIC | 4747.0076 – h – (in) | Thickness – s – (in) | Sectional Area (in 2 ) | Weight (lb f /ft) | Moment of Inertia – I x – (in 4 ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 x 12 | 12 | 1 3/8 | 30. 9 9 | 105 | 410.0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 1 1/4 | 28.3 | 96.4 | 377.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 1 1/8 | 25.6 | 87.2 | 344.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 1 | 22.9 | 77.8 | 310.4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 x 10 | 10 | 1 3/8 | 25.6 | 87.1 | 232.1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 1 1/4 | 23.5 | 79.9 | 215.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 1 1/8 | 21.2 | 72.3 | 196.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 1 | 19.0 | 64.7 | 177.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 7/8 | 16.7 | 56.9 | 157.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 3/4 | 14.4 | 49.1 | 137.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 x 8 | 8 | 1 1/8 | 16. 7 7 | 56.9 | 98.0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 1 | 15.0 | 51.0 | 89.0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 7 /8 | 13.2 | 45.0 | 79.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 3/4 | 11.4 | 38.9 | 69.7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 5/8 | 9.6 | 32.7 | 59.4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 9/16 | 8.7 | 29.6 | 54.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 1/2 | 7.8 | 26.4 | 48.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 x 6 | 6 | 1 | 11.0 | 37.4 | 35.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 7/8 | 9.7 | 33.1 | 31.9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 3/4 | 8.4 | 28.7 | 28.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 5/8 | 7. 1 1 | 24.2 | 24.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 9/16 | 6.4 | 21.9 | 22.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 1/2 | 5.8 | 19.6 | 19.9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 7/16 | 5.1 | 17.2 | 17.7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 3/8 | 4.4 | 14.9 | 15.4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 5/16 | 3.7 | 12.4 | 13.0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 x 5 | 5 | 7 /8 | 8.0 | 27.2 | 17.8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 3/4 | 6.9 | 23.6 | 15.7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 5/8 | 5.9 | 20.0 | 13.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 1/2 | 4.8 | 16.2 | 11.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 7/16 | 4. 2 2 | 14.3 | 10.0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 3/8 | 3.6 | 12.3 | 8.74 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 5/16 | 3.0 | 10.3 | 7.42 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 x 4 | 4 | 3/4 | 5.4 | 18.5 | 7.67 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 5/8 | 4.6 | 15.7 | 6.66 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 1/2 | 3.8 | 12.8 | 5.56 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 7/16 | 3.3 | 11.3 | 4.97 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 3/8 | 2.9 | 9.8 | 4.36 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 5/16 | 2.4 | 8.2 | 3.71 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 1/4 | 1.9 | 6.6 | 3.04 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 1/2 x 3 1/2 | 3 1/2 | 1/2 | 3. 3 3 | 11.1 | 3.64 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 1/2 | 7/16 | 2.9 | 9.8 | 3.26 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 1/2 | 3/8 | 2,5 | 8.5 | 2.87 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 1/2 | 5/16 | 2.1 | 7.2 | 2.45 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 1/2 | 1/4 | 1.7 | 5.8 | 2.01 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 x 3 | 3 | 1/2 | 2.75 | 9.4 | 2.22 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 7/16 | 2.43 | 8.3 | 1.99 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 3/8 | 2.11 | 7.2 | 1.76 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 5/16 | 1.78 | 6.1 | 1.51 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 1/4 | 1.44 | 4.9 | 1,24 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 3/16 | 1,09 | 3,7 | 0,96 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 1/2 1/2 | 99 2 | 92929292929292 | 1111182929999999999999999999 | 1189999999999999999999999999999999999999999999999999999999999999999999. | 9 2| . 7,7 | 1.23 | 2 1/2 | 3/8 | 1.73 | 5.9 | 0.98 | 2 1/2 | 5/16 | 1.46 | 5.0 | 0.85 | 2 1/2 | 1/4 | 1.19 | 4.1 | 0.70 | 2 1/2 | 3/16 | 0.90 | 3.1 | 0.55 | 2 x 2 | 2 | 3/8 | 1.36 | 4.7 | 0.48 | 2 | 5/16 | 1.15 | 3.9 | 0.42 | 2 | 1/4 | 0.94 | 3.2 | 0,35 | 2 | 3/16 | 0,72 | 2,4 | 0,27 | 2 | 1/87242 | 2 | ,10032 | 2 | 1/8 | 2 | ,1892 | 2 | 10032 | 2 | 10032 | . | 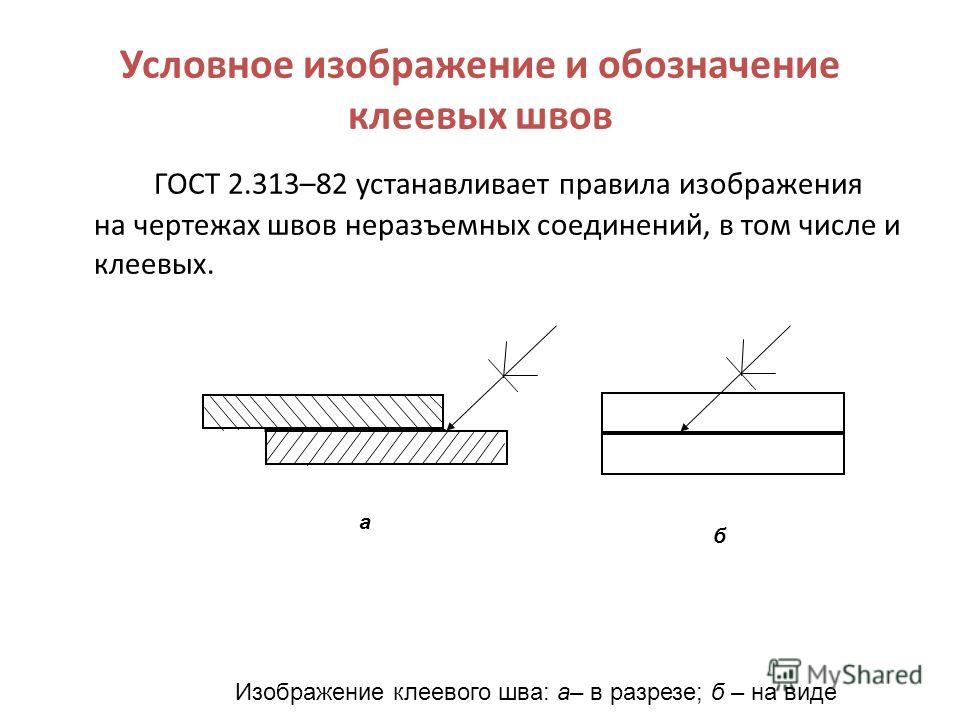 0628 0628 |
- 1 в = 25,4 мм
- 1 см 4 = 10 -8 М = 10 4 мм
- 33 4 мм
- 31 1 мМ
- 31 1 мм
- 33 4 мм
- 33 4 мм 9 9000 133 4 мм 9 4 мм 9 = 41,6 см 4
- 1 см 3 = 10 -6 М 3 = 10 3 ММ 3 = 10 3 мм 3 3 мм 3 3 мм 3 3 мм 3 3 мм 3 ММ 3 3 ММ 3 ММ 2 x 1/4 – указывает угол 2 дюйма глубокая и широкая – и 1/4 дюйма толстая.
Рекламные ссылки
Связанные темы
Связанные документы
Engineering ToolBox — Расширение SketchUp — 3D-моделирование в режиме онлайн!
Добавляйте стандартные и настраиваемые параметрические компоненты, такие как балки с полками, пиломатериалы, трубопроводы, лестницы и т.
 д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, интересными и бесплатными приложениями SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!
д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, интересными и бесплатными приложениями SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!Перевести
О Engineering ToolBox!
Мы не собираем информацию от наших пользователей. В нашем архиве сохраняются только электронные письма и ответы. Файлы cookie используются только в браузере для улучшения взаимодействия с пользователем.
Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложений на локальном компьютере. Эти приложения будут — из-за ограничений браузера — отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные.
Google использует файлы cookie для показа нашей рекламы и обработки статистики посетителей. Пожалуйста, прочитайте Конфиденциальность и условия Google для получения дополнительной информации о том, как вы можете контролировать показ рекламы и собираемую информацию.



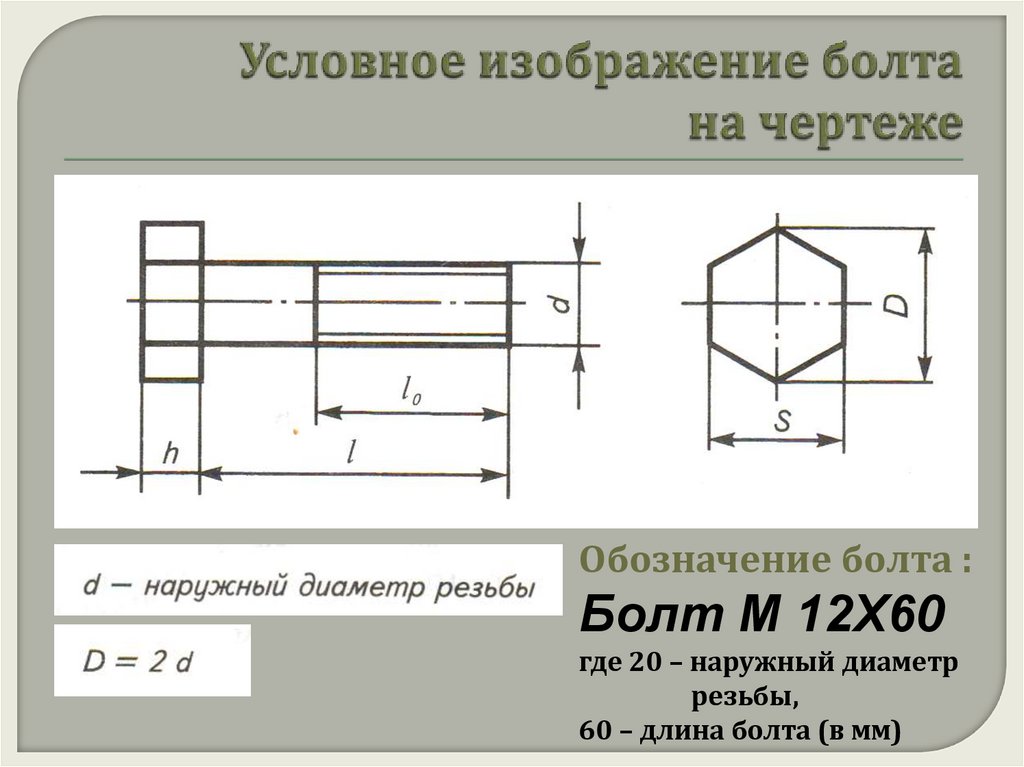
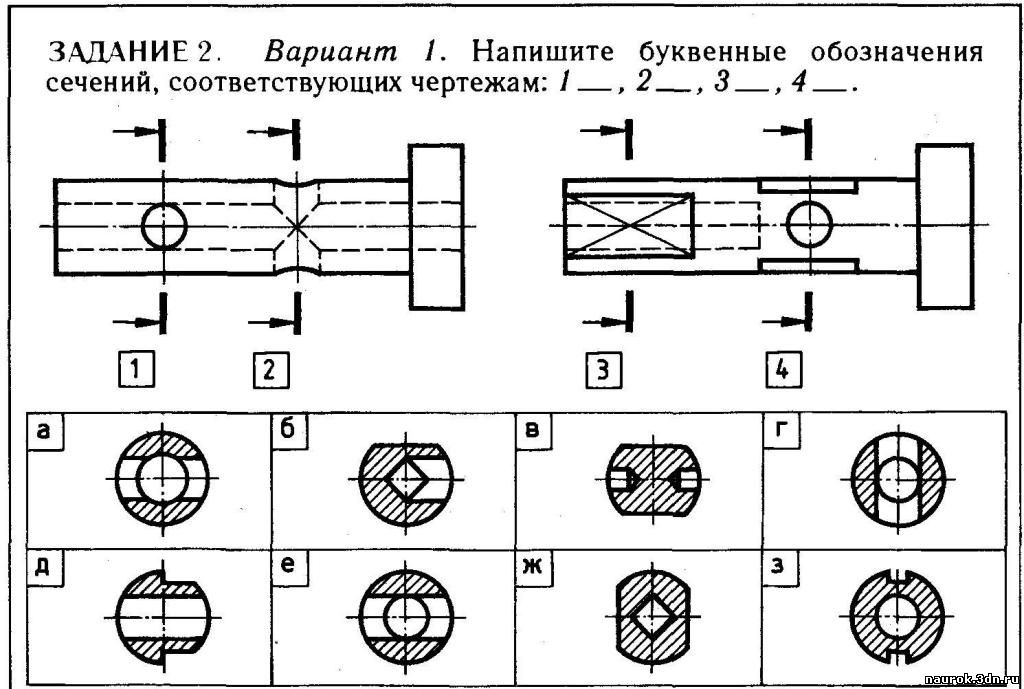 ru/wp-content/uploads/2022/08/test.svg"},"grouper-22":{"type":"grouper","labels":["Внутренний угол","Наружный угол"],"items":[["$\\angle{\\alpha}$","$\\angle{CAB}$","$\\angle{(ab)}$","$\\angle{A}$"],["$\\angle{\\phi}$","$\\angle{BAC}$","$\\angle{(ba)}$"]]}}}]}
ru/wp-content/uploads/2022/08/test.svg"},"grouper-22":{"type":"grouper","labels":["Внутренний угол","Наружный угол"],"items":[["$\\angle{\\alpha}$","$\\angle{CAB}$","$\\angle{(ab)}$","$\\angle{A}$"],["$\\angle{\\phi}$","$\\angle{BAC}$","$\\angle{(ba)}$"]]}}}]}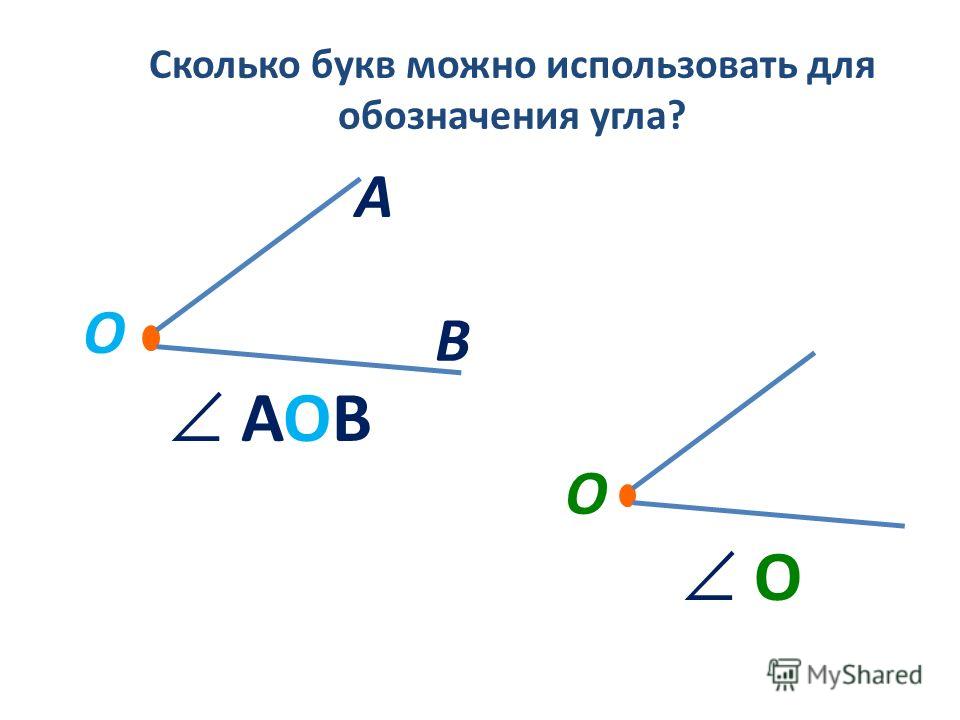 Главная улица;
Берриен Спрингс, Мичиган 49103-1013
Главная улица;
Берриен Спрингс, Мичиган 49103-1013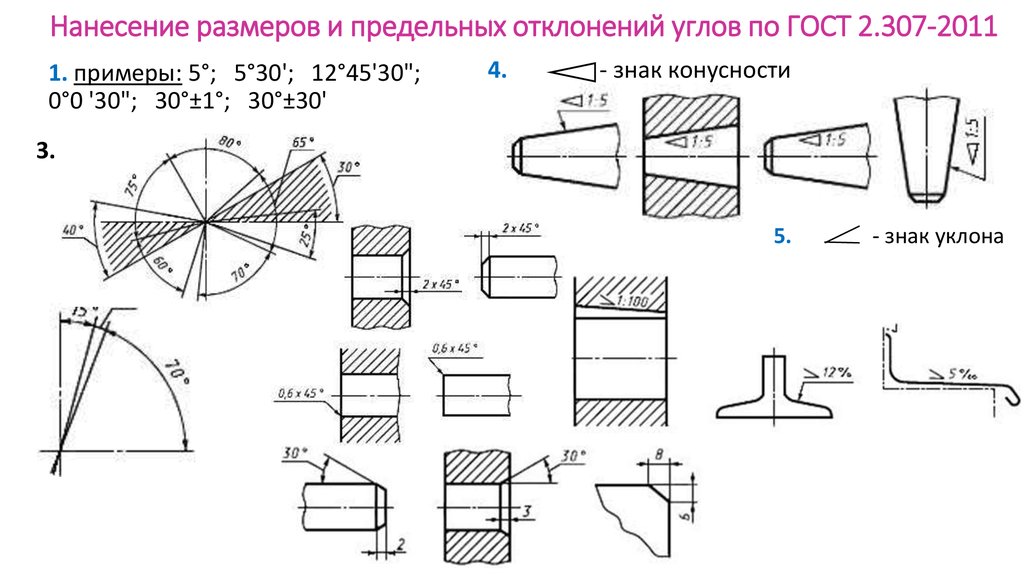 д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, интересными и бесплатными приложениями SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!
д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, интересными и бесплатными приложениями SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!