как обозначить и измерить углы, правила
Определение
Геометрия — это раздел математики, который занимается изучением форм и их измерений. Он также фокусируется на относительной конфигурации форм и их пространственных свойствах.
Все геометрические фигуры состоят из точек, линий, лучей и плоской поверхности. Когда две линии или лучи сходятся в одной точке, измерение между двумя линиями называется углом. В этой статье мы собираемся обсудить, что такое угол, каковы различные типы углов и их значение с примерами.
Определение угла в математике
Определение
Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.
Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.
Стороны угла – лучи, которые образуют угол (А, В).
Вершина угла – точка, из которой выходят лучи (О).
Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.
Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.
- Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
- Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.
Интересно
Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».
Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.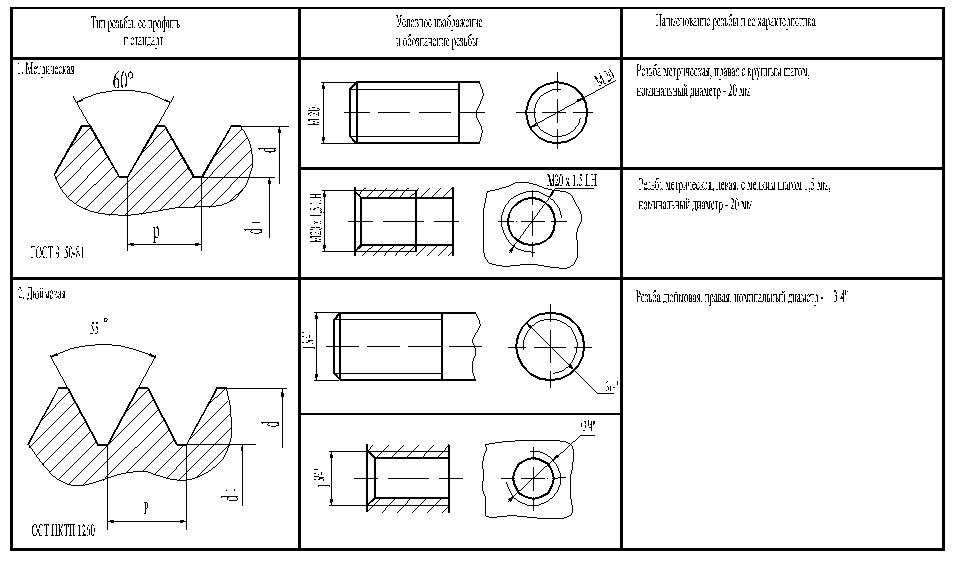
Как обозначить углы?
Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:
- Способ 1:
Как правило, угол обозначается строчными буквами, такими как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д. - Способ 2:
Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).
Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.
Типы углов
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
- Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
- Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.

Прямой угол можно легко наблюдать, так как он образует форму буквы L. - Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
это тупой угол. - Развернутый угол — угол, образованный прямой линией, называется прямым углом. Это
половина полного оборота круга. Размер прямого угла равен 180°. - Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
- Полный угол — когда измерение угла равно 360 градусам, это полный угол.
Ряд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.
Углы образованные при пересечении двух прямых
При пересечении двух прямых образуются два вида углов:
- смежные;
- вертикальные.
Смежные углы
Определение
Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.
Смежные углы между собой дополняемые, так как являются продолжением один другого.
Свойства смежных углов
- Сумма смежных углов равна 180°
- Если оба смежных угла равны между собой, то они являются прямыми.
- В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
- Синусы смежных углов равны.
- Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.
Вертикальные углы
Определение
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Пример:
Пары углов 1 и 3; 2 и 4 – являются вертикальными
По свойству вертикальных углов:
\[\angle C O D=\angle A O B\]
\[\angle B O D=\angle A O C\]
Пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1 — являются смежными
По свойству смежных углов:
\[\angle C O D+\angle D O B=180^{\circ}\]
\[\angle D O B+\angle B O A=180^{\circ}\]
\[\angle B O A+\angle A O C=180^{\circ}\]
\[\angle A O C+\angle C O D=180^{\circ}\]
| Смежные углы | Вертикальные углы |
Два угла с общей стороной и вершиной называются смежными.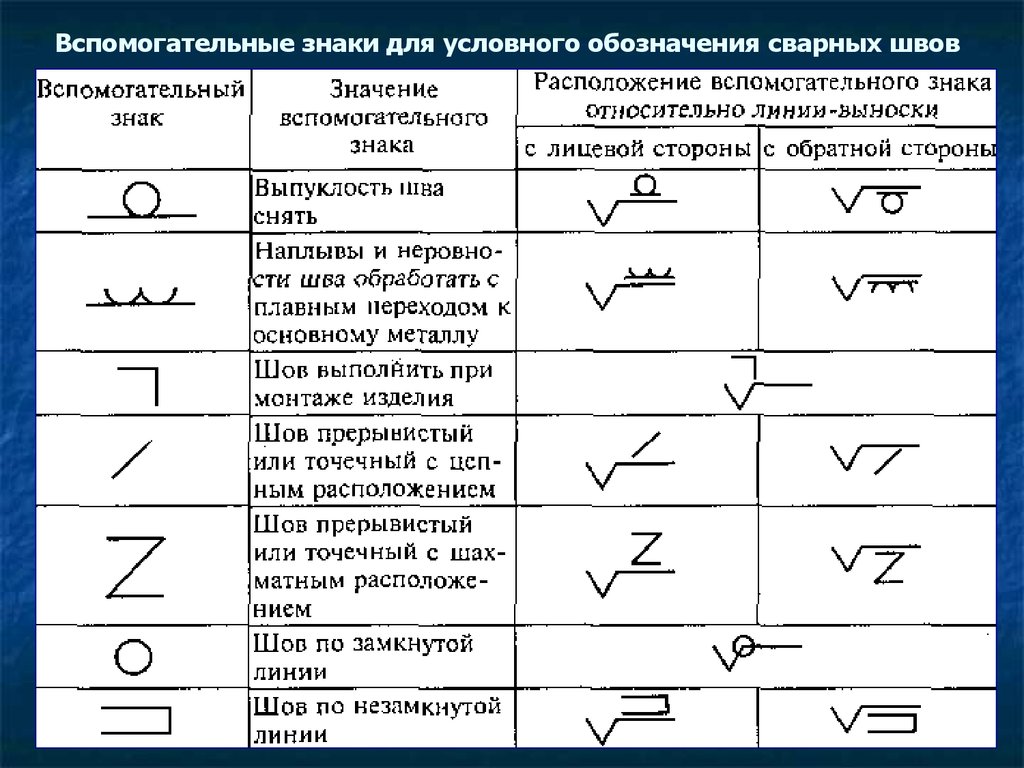 | Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами. |
| Имеют общую сторону и общую вершину. | Имеют общую вершину, но не имеют общую сторону |
| Смежные углы не всегда равны по величине | Вертикально противоположные углы равны по величине |
Сравнение углов
Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:
\[\angle A_{1} O_{1} B_{1}\] и \[\angle A_{2} O_{2} B_{2}\] полностью совмещаются при наложении следовательно: \[\angle A_{1} O_{1} B_{1}=\angle A_{2} O_{2} B_{2}\]
\[\angle A_{1} O_{1} B_{1}\] и \[ \angle A_{2} O_{2} B_{2}\] не совмещаются при наложении: \[\angle A_{1} O_{1} B_{1} \neq \angle A_{2} O_{2} B_{2}\]
Причем: \[\angle A_{1} O_{1} B_{1}<\angle A_{2} O_{2} B_{2}\]
При этом развернутые углы всегда являются равными.
Совмещение углов \[\angle A B C\] и \[\angle M N K\] происходит следующим образом:
- Вершину B одного угла совмещаем с вершиной N другого угла.
- Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.
Если нет, то один угол — меньше другого: ∠ABC<∠MNK.
Некоторые важные теоремы, основанные на прямых и углах:
- Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
- Вертикальные углы равны, когда прямая пересекает прямые.
 Линии могут быть как параллельными, так и непараллельными.
Линии могут быть как параллельными, так и непараллельными.
Измерение углов
Существует несколько единиц измерения углов. Рассмотрим наиболее часто используемые единицы измерения:
Градусная мера
Полный оборот, т. е. когда начальная и конечная стороны находятся в одном и том же положении после вращения по часовой стрелке или против часовой стрелки, делится на 360 единиц, называемых градусами. Итак, если поворот от начальной стороны к конечной стороне составляет \[\left(\frac{1}{360}\right)\] оборота, то говорят, что угол имеет меру в один градус. Обозначается как 1°.
Мы измеряем время в часах, минутах и секундах, где 1 час = 60 минут, а 1 минута = 60 секунд. Точно так же при измерении углов
- 1 градус = 60 минут, обозначаемый как 1° = 60′.
- 1 минута = 60 секунд, обозначаемая как 1 ′ = 60 ″.
Радианная мера
Радианная мера немного сложнее, чем градусная. Представьте круг с радиусом 1 единица.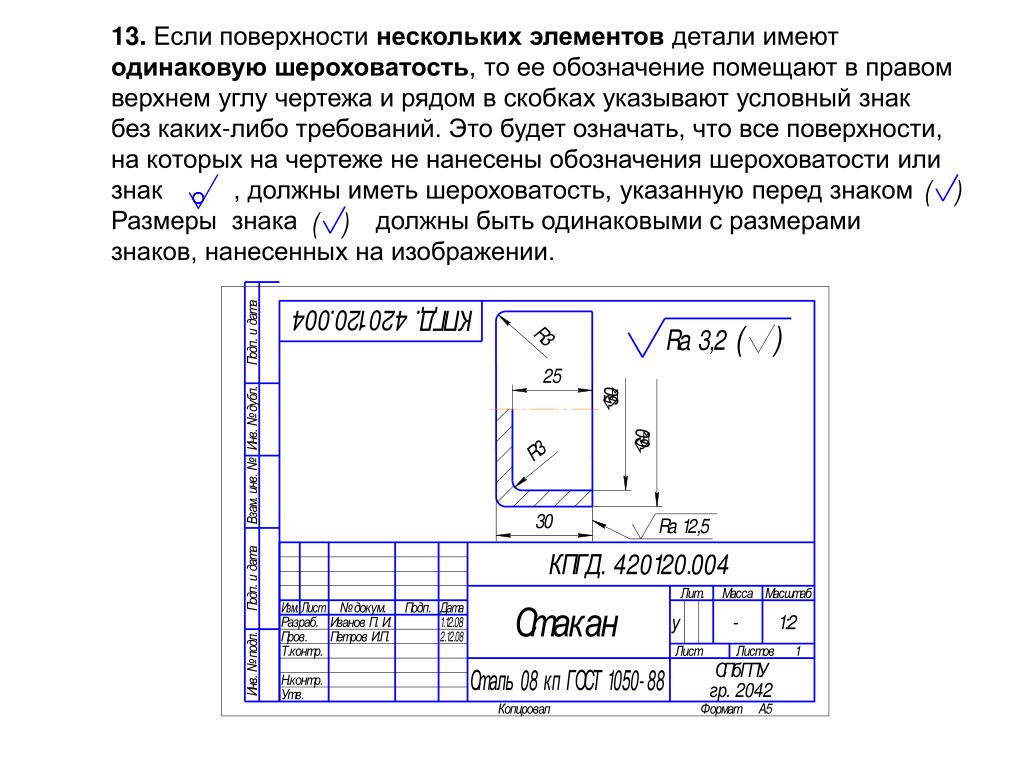 Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
Вот еще несколько примеров углов: -1 радиан, радиан, \[1 \frac{1}{2}\] радиан, \[-1 \frac{1}{2}\] радиан.
Длина окружности = \[2 \pi r \ldots\] где r — радиус окружности. Следовательно, для круга с радиусом 1 единица длины окружности равна \[2 \pi\]. Следовательно, один полный оборот начальной стороны образует в центре угол \[2 \pi\] радиан. Обобщая это, имеем:
В окружности радиуса r дуга длины r образует угол в 1 радиан в центре. Следовательно, в окружности радиуса r дуга длины l будет опираться на угол = \[\frac{l}{r}\] радиан. Обобщая это, мы имеем в окружности радиуса r, если дуга длины l образует угол θ радиан в центре, то:
\[\theta=\frac{l}{r}\]
\[l=r \theta\]
Связь между степенью и радианными мерами
По определениям степени и радиана мы знаем, что угол, образуемый окружностью в центре, равен:
- 360° – по градусной мере
- \[2 \pi\] радиан — в радианах
Следовательно, \[2 \pi\] радиан = 360° ⇒ \[\pi\] радиан = 180°. {\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.
{\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как измерить угол
Для измерения углов используется транспортир:
ТранспортирПопробуем измерить угол \[\angle A O B\]
Шаги для измерения угла \[\angle \mathrm{AOB}\].
Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°
Далее попробуем измерить этот ∠AOC:
Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.
Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC. Таким образом, ∠ AOC = 143°
Таким образом, ∠ AOC = 143°
Как построить углы
Используем транспортир для построения углов. Нарисуем угол 50°.
Шаг 1: сначала нарисуйте луч OB и совместите транспортир с OB, как показано.
Шаг 2: поместите точку над отметкой на транспортире, которая соответствует 50°.
Шаг 3: Уберите транспортир и нарисуйте луч, начинающийся в точке О и проходящий через эту точку. Таким образом, ∠AOB – искомый угол, т.е. ∠AOB = 50°.
Примечание. Если луч идет в другом направлении, мы измеряем угол от отметки 0° в левом нижнем углу.
На изображении ниже показано, как нарисовать угол 50°, когда луч указывает в другом направлении.
Обозначение углов на чертеже
Для комфортного отображения дуг, углов применяют чертежи. Не всегда возможно грамотно изобразить и обозначить тот или другой угол, дугу или наименование. Равные углы имеют определение в виде идентичного числа дуг, а неравноценные в виде различного.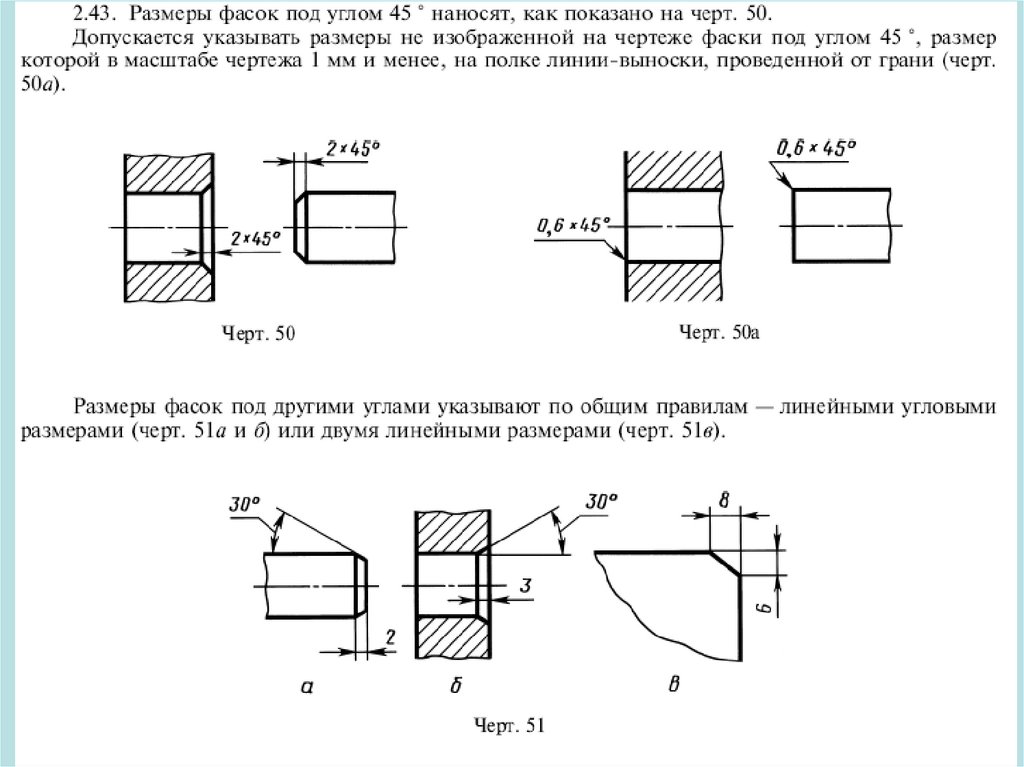
На чертеже запечатлено корректное обозначение острых, равных и неравных углов.
Если нужно обозначить более трех углов, то применяются специальные обозначения дуг, например, зубчатые или волнистые, но в принципе это не имеет особого значения.
Обозначение углов должно быть простым, чтобы не препятствовать иным значениям. При решении задачи рекомендовано обозначать только нужные для решения углы, чтобы не перегружать весь чертеж. Это не помешает решению задачи, а также придаст эстетичный облик чертежу.
размеры на чертежах, обозначения на чертежах
Размеры на чертежах. Размеры чертежей по ГОСТ2.307-68
Для определения величины изображенного изделия и его элементов служат размерные числа, нанесенные на чертеже.
Исключение составляют случаи, предусмотренные в ГОСТ 2.414-75; ГОСТ 2.417-78; ГОСТ 2.419-68, когда величину изделия или его элементов определяют по изображениям, выполненным с достаточной степенью точности.
Требуемая точность изделия при изготовлении задается указанием на чертеже предельных отклонения размеров, а также предельных отклонений формы и расположения поверхностей.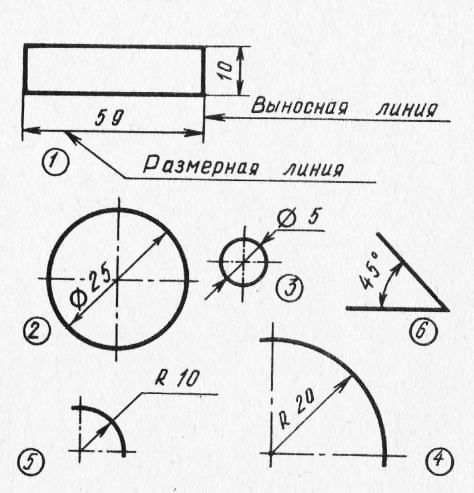
Общее количество размеров на чертеже должно быть минимальным, но достаточным для изготовления и контроля изделия.
Справочные размеры на чертеже отмечают знаком «*», а в технических требованиях записывают: «* Размеры для справок». Если все размеры на чертеже справочные, их знаком «*» не отмечают, а в технических требованиях записывают: «Размеры для справок».
На чертежах изделий у размеров, контроль которых технически затруднен; наносят знак «*», а в технических требованиях помещают надпись «Размеры обеспеч. инстр.». Указанная надпись означает, что выполнение заданного чертежом размера с предельным отклонением должно гарантироваться размером инструмента или соответствующим технологическим процессом.
Не допускается повторять размеры одного и того же элемента на разных изображениях, в технических требованиях, основной надписи и спецификации. Исключение составляют справочные размеры (перенесенные с чертежей изделий-заготовок, размеры деталей (элементов) из сортового, фасонного, листового и др. проката).
проката).
Линейные размеры на чертежах и их предельные отклонения на чертежах и в спецификациях указывают в миллиметрах, без обозначения единицы измерения. Если на чертеже размеры необходимо указать не в миллиметрах, а в других единицах измерения (сантиметрах, метрах и т.д.), то соответствующие размерные числа записывают с обозначением единицы измерения (см, м) или указывают их в технических требованиях.
Размеры на чертежах ГОСТ 2.307-68 указывают размерными числами (в мм) и размерными линиями. Общее количество размеров на чертеже должно быть минимальным, но достаточным для изготовления изделия. Не допускается повторять размеры одного и того же элемента на разных изображениях.
Размеры наносят от общей базы
от нескольких баз
цепочкой
Не допускается наносить размеры на чертежах в виде замкнутой цепи, за исключением случая, когда один размер указан как справочный (со звездочкой).
В случае, если деталь или элемент детали симметричны размер ставится относительно оси симметрии
Для размеров чертежей и предельных отклонений, приводимых в технических требованиях и пояснительных надписях на поле чертежа, обязательно указывают единицы измерения.
Угловые размеры чертежей и предельные отклонения угловых размеров указывают в градусах, минутах и секундах с обозначением единицы измерения, например: 4°;
Размерные и выносные линии следует выполнять сплошными тонкими линиями. Размерные линии ограничены стрелками. Величина стрелок выбирается в зависимости от толщины S линии видимого контура предмета и должна быть приблизительно одинакова для всех размерных линий чертежа.
При нанесении размера на чертеже угла размерную линию проводят в виде дуги с центром в его вершине, а выносные линии – радиально
При нанесении размеров нужно помнить, что на всех чертежах не зависимо от масштаба указываются действительные размеры изделия.
Размерные числа в пределах одного чертежа выполняют шрифтом одного размера. Размерные числа наносят над размерной линией возможно ближе к её середине. При нанесении нескольких параллельных или концентричных размерных линий на небольшом расстоянии друг от друга размерные числа над ними рекомендуется располагать в шахматном порядке
При нанесении размера диаметра внутри окружности размерные числа смещают относительно середины размерных линий. Если необходимо нанести размер в заштрихованной зоне, соответствующее размерное число наносят на полке линии-выноски
Если необходимо нанести размер в заштрихованной зоне, соответствующее размерное число наносят на полке линии-выноски
Стрелки, ограничивающие размерные линии должны упираться острием в соответствующие линии контура, или выносные, или осевые линии.
Выносные линии должны выходить за концы размерных стрелок на 1…5 мм
Минимальное расстояние между параллельными размерными линиями должно быть 7 мм, а между размерной и линией контура – 10 мм и выбраны в зависимости от размеров изображения и насыщенности чертежа .
Необходимо избегать пересечения размерных и выносных линий.
Не допускается использовать линии контура, осевые, центровые и выносные линии в качестве размерных.
Допускается проводить размерные линии непосредственно к линиям видимого контура, осевым, центровым и другим линиям.
Выносные линии проводят от линии видимого контура, за исключением случаев, когда при нанесении размеров на невидимом контуре отпадает необходимость в вычерчивании дополнительного изображения.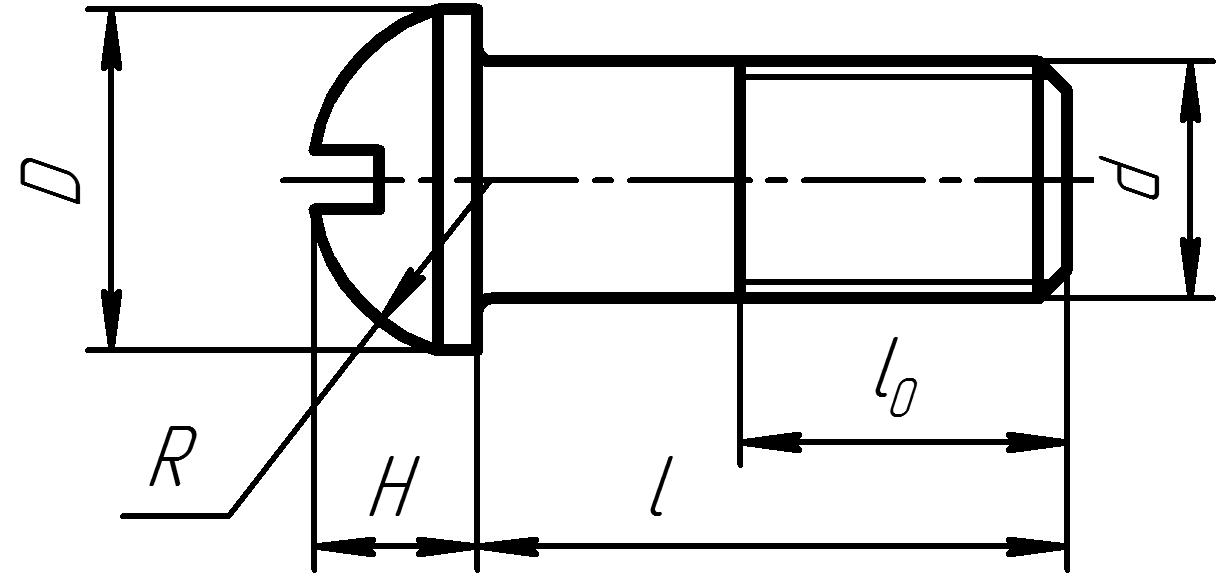
Если вид или разрез симметричного предмета или отдельных симметрично расположенных элементов изображают только до оси симметрии или с обрывом, то размерные линии, относящиеся к этим элементам, проводят с обрывом, и обрыв размерной линии делают дальше оси или линии обрыва предмета (рис.18).
Размеры на чертежах. Размерные линии допускается проводить с обрывом в следующих случаях:
а) при указании размера диаметра окружности независимо от того, изображена ли окружность полностью или частично, при этом обрыв размерной линии делают дальше центра окружности
б) при нанесении размеров от базы, не изображенной на данном чертеже
При изображения изделия с разрывом размерную линию не прерывают
При недостатке места для стрелок на размерных линиях, расположенных цепочкой, стрелки допускается заменить засечками, наносимыми под углом 45° к размерным линиям или четко наносимыми точками.
При недостатке места для стрелки из-за близко расположенной контурной или выносной линии последние допускается прерывать.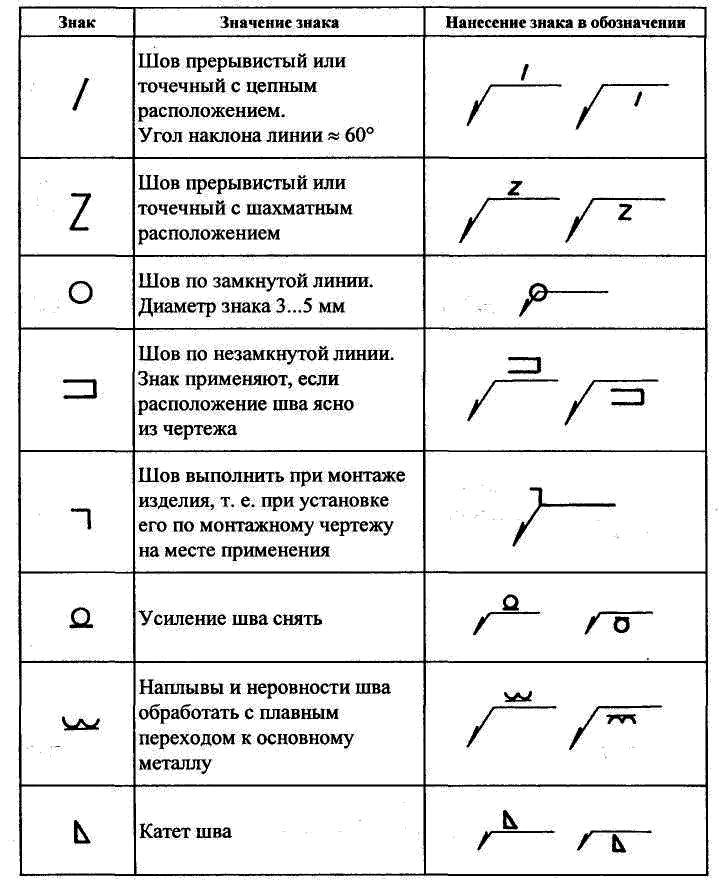
Способ нанесения размерного числа при различных положениях размерных линий (стрелок) на чертеже определяется наибольшим удобством чтения.
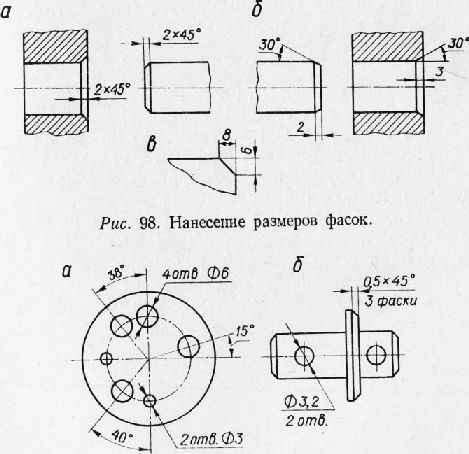
Специальные размеры чертежей.
Уклон- это наклон одной линии относительно другой; измеряется отношением катетов прямоугольного треугольника CB : AB = 1 : 5.
Конусность – это отношение диаметра конуса к его высоте k = ( D – d ) / L. Конусность и уклон выражаются отношением двух чисел или в процентах.
Сопряжение – это плавный переход от одной линии к другой с помощью сопрягающей дуги.
Построить сопряжение – это значит найти центры сопрягаемых дуг и точки сопряжения.
Существует огромное количество различных сопряжений, применяемых при описании плоских деталей.
Основные правила таких сопряжений даны во многих учебниках и справочниках по черчению.
В автоматизированных системах такие сопряжения выполняются автоматически.
Обозначения на чертежах.
Графические обозначения материалов в сечениях см. ГОСТ 2.306-68. Металлы и твердые сплавы в сечении на комплексных чертежах обозначаются штриховкой линий под углом 45° . Если линии штриховки совпадают с линией контура, угол берется 30° или 60° . Линии штриховки наносят в одну и ту же сторону (с одинаковой частотой 1…10 мм) на всех проекциях детали. Ребра жесткости при разрезе вдоль не штрихуются. В аксонометрических проекциях штриховка выполняется по правилу треугольника или диагонали ромба, построенного на аксонометрических осях, см. ГОСТ 2.317-69
ГОСТ 2.306-68. Металлы и твердые сплавы в сечении на комплексных чертежах обозначаются штриховкой линий под углом 45° . Если линии штриховки совпадают с линией контура, угол берется 30° или 60° . Линии штриховки наносят в одну и ту же сторону (с одинаковой частотой 1…10 мм) на всех проекциях детали. Ребра жесткости при разрезе вдоль не штрихуются. В аксонометрических проекциях штриховка выполняется по правилу треугольника или диагонали ромба, построенного на аксонометрических осях, см. ГОСТ 2.317-69
Обозначение на чертежах шероховатости поверхности.
ГОСТ 2789-73 устанавливает параметры шероховатости Ra и Rz. Rz = (y1+ y2+…+ yn) / n – среднее арифметическое абсолютных значений отклонений профиля в пределах базовой длины, где y – расстояние между любой точкой профиля и средней линией; n – число значений y.(рис.1)
Rz = (h2min +…+ h3min) / 5 – среднее арифметическое абсолютных значений отклонений точек пяти наибольших максимумов и пяти наибольших минимумов профиля .
Степень шероховатости поверхности определяется ее классом чистоты. При этом Ra указывается без символа, а Rz – с символом.
Чистота поверхности зависит от способа обработки и инструмента, которым выполняется та или иная технологическая операция.
ГОСТ 2.309 – 73 устанавливает обозначение шероховатости поверхностей и правила нанесения их на чертежах изделий. Высота h (cм. рисунок) знаков шероховатости равна высоте размерных чисел, высота Н равна 1,5 – ….. 3h. Толщина линий знаков равна половине толщины основной линии.
Обозначения на чертежах
Знак (рис,а) применяют для обозначения шероховатости поверхности, не устанавливаемой конструктором. Знак (рис.,б) применяют для поверхности, образованной удалением слоя материала (точением, сверлением и т.п.). Знак (рис,в) для поверхности, образованной литьем, ковкой и т.п. (т.е. без удаления слоя материала).
На рис. показана структура обозначения шероховатости. Вид обработки поверхности указывается только в случае ее единственности.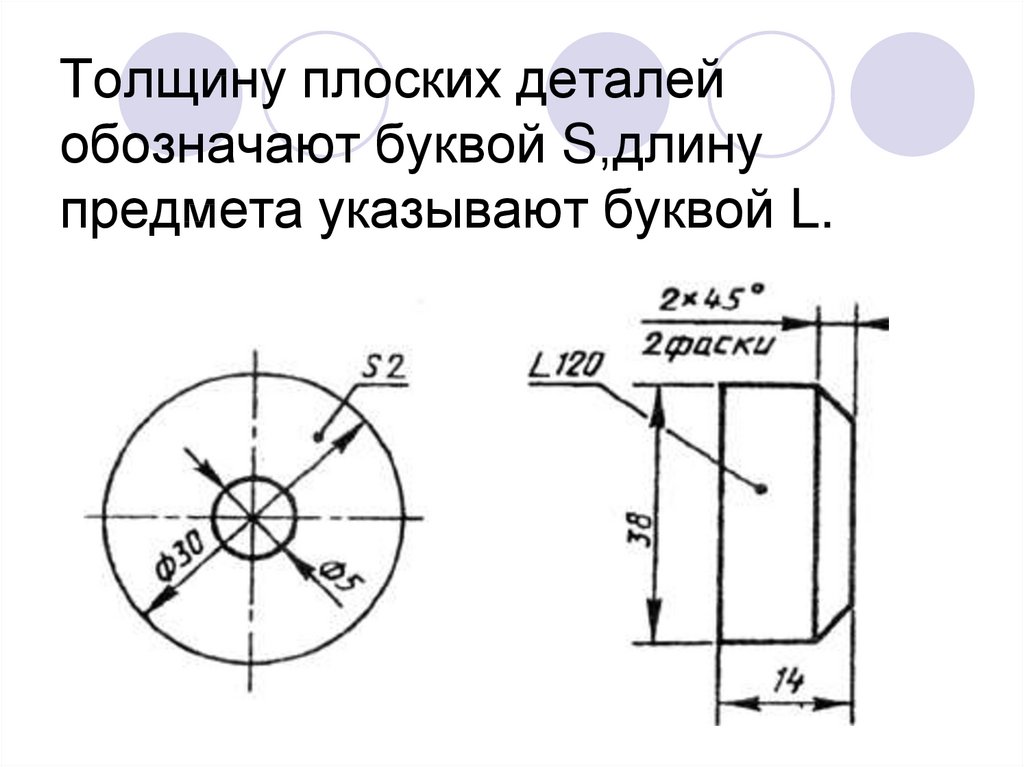 Направление неровностей приводят только при необходимости.
Направление неровностей приводят только при необходимости.
Обозначение на чертежах шероховатости (рис) располагают на линиях контура, выносных линиях или на полках линий-выносок, а при недостатке места – на размерных линиях или их продолжении. Если знак имеет полку, обозначение шероховатости располагают относительно основной надписи (рис.,а), без полки – рис.,б. Если изображение с разрывом, то знак наносят ближе к месту, где указан размер.
Обозначение шероховатости поверхностей зубчатых колес, эвольвентных колес, и т.д. условно наносят на линии делительной поверхности. Шероховатость профиля резьбы наносят на выносной линии, размерной линии или ее продолжении. Если шероховатость поверхности различна, то поверхность разграничивают сплошной тонкой линией и наносят размеры и знаки шероховатости на каждом участке.
При указании одинаковой шероховатости для всех поверхностей изделия обозначение помещают в правом верхнем углу чертежа (рис). Размеры знака в обозначении больше, чем на чертеже, в полтора раза.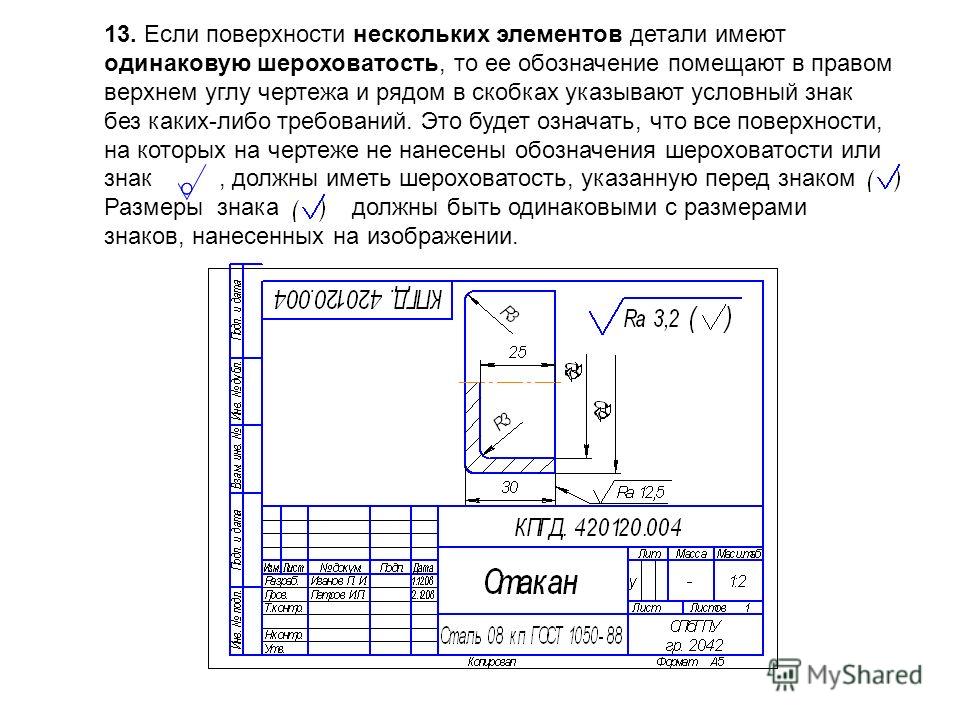
Кроме изображения предмета с размерами чертеж может содержать: а) текстовую часть, состоящую из технических требований и (или) технических характеристик; б) надписи с обозначениями изображений, а также относящиеся к отдельным элементам изделия; в) таблицы с размерами и другими параметрами, техническими требованиями, условными обозначениями и т.д. Выполнение основной надписи чертежа должно производиться в соответствии с требованием ГОСТ 2.104-68 и ГОСТ 2.109- 68. Содержание текста должно быть кратким и точным, не должно быть сокращений слов за исключением общепринятых и установленных в стандартах. Текст на поле чертежа, таблицы, надписи, как правило, изображают параллельно основной надписи чертежа.
Обозначения на чертежах надписей
Около изображений на полках линий-выносок наносят только краткие надписи, например, указание о количестве элементов (отверстий, канавок и т.п.). Линию – выноску, пересекающую контур изображения и не отводимую от какой-либо линии, заканчивают точкой. Линию-выноску, отводимую от линии видимого и невидимого контура, изображенного основной и штриховой линией, заканчивают стрелкой. На конце линий-выносок, отводимых от всех других линий, не должно быть ни стрелки, ни точки. Линии-выноски не должны пересекаться между собой, быть непараллельными линиями штриховки. По возможности, они не должны пересекать размерные линии и элементы изображения. Допускается выполнять линии-выноски с одним изломом, а также проводить от одной полки две и более линии-выноски. Надписи, относящиеся к изображению, могут содержать не более двух строк, располагаемых над полкой линии-выноски и под ней.
Линию-выноску, отводимую от линии видимого и невидимого контура, изображенного основной и штриховой линией, заканчивают стрелкой. На конце линий-выносок, отводимых от всех других линий, не должно быть ни стрелки, ни точки. Линии-выноски не должны пересекаться между собой, быть непараллельными линиями штриховки. По возможности, они не должны пересекать размерные линии и элементы изображения. Допускается выполнять линии-выноски с одним изломом, а также проводить от одной полки две и более линии-выноски. Надписи, относящиеся к изображению, могут содержать не более двух строк, располагаемых над полкой линии-выноски и под ней.
Обозначения на чертежах текста.
Текстовую часть, помещенную на поле чертежа, располагают над основной надписью. Межу текстовой и основной надписями не допускается помещать изображения, таблицы и т.п. На листах формата более А4 допускается размещение текста в две и более колонки. Ширина колонки должна быть не более 185 мм. Таблицы размещают на свободном поле чертежа (за исключением тех случаев, где стандартом это место установлено, например, для зубчатых колес, червяка, шлицевого вала и т.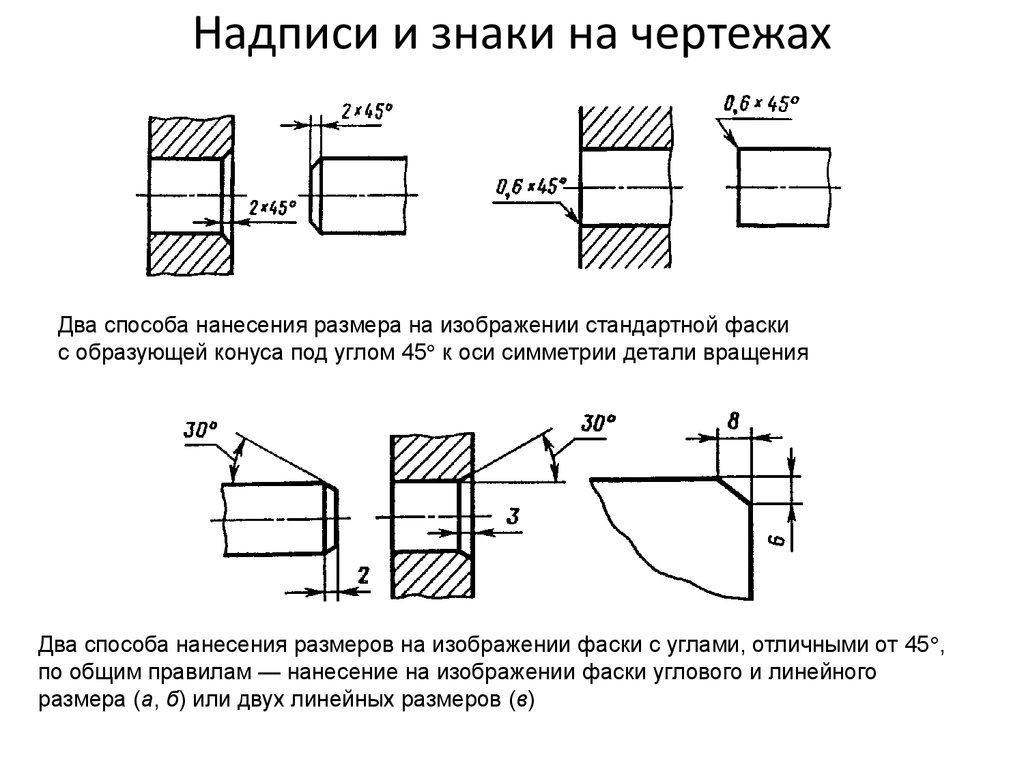 п.) справа от изображения или ниже его и выполняют по ГОСТ 2.105-68.
п.) справа от изображения или ниже его и выполняют по ГОСТ 2.105-68.
Обозначения на чертежах изображений.
Для обозначения на чертеже изображений (видов, разрезов, сечений), поверхностей, размеров и других элементов изделия применяют прописные буквы русского алфавита, за исключением букв Й, О, Х, Ъ, Ь, Ы. Размер шрифта буквенных обозначений должен быть больше размера цифр размерных чисел, примерно в два раза. Масштаб изображений на чертеже, отличающийся от указанного в основной надписи, указывают непосредственно под надписью, относящейся к изображению.
Harmony 20 Premium Документация: Замены имен чертежей
Мы рекомендуем использовать соглашение об именах для ваших чертежей. Особенно, если вы объединяете все ракурсы персонажа в одной и той же сцене разбивки, рекомендуется идентифицировать каждый используемый ракурс.
HAR_Essentials_NOT”> Прежде чем разбивать символы для вашего производства, мы рекомендуем вам создать соглашение об именах чертежей, которое представляет используемый угол. Например, используйте «f» для обозначения лицевой стороны, «s» для обозначения стороны, «q» для обозначения трех четвертей, чтобы имя чертежа выглядело следующим образом: f1, f2, f3, s1, s2 и т. д. Это будет весьма полезно во время замена анимации и рисунков. Поскольку чертежи отображаются в алфавитном и числовом порядке, все чертежи для вида спереди будут вместе, затем все чертежи для вида в три четверти и так далее.Имейте в виду, что в библиотеке замены рисунков рисунки отображаются в алфавитном порядке. Если вы хотите, чтобы они располагались в определенном порядке, убедитесь, что вы назвали их соответствующим образом.
Как добавить префикс к одному или нескольким рисункам
- На временной шкале выберите диапазон чертежей, который нужно переименовать.

- Выполните одно из следующих действий:
| ‣ | Щелкните правой кнопкой мыши выделенный элемент и выберите “Чертежи” > “Переименовать чертеж с префиксом”. |
| ‣ |  |
Откроется диалоговое окно «Переименовать чертеж с префиксом».
- Введите символы, которые вы хотите добавить перед текущим именем чертежа.
- Щелкните OK .
ПРИМЕЧАНИЕ Чтобы переименовать чертеж, выберите его и используйте параметр «Переименовать чертеж». Ctrl + D (Windows/Linux) или ⌘ + D (Mac OS X). или . Не делайте двойной щелчок по кадру
и не пишите новое имя, так как это создаст новый рисунок и скроет ваш текущий. Обратите внимание, что скрытый чертеж не был удален и по-прежнему находится в папке элемента.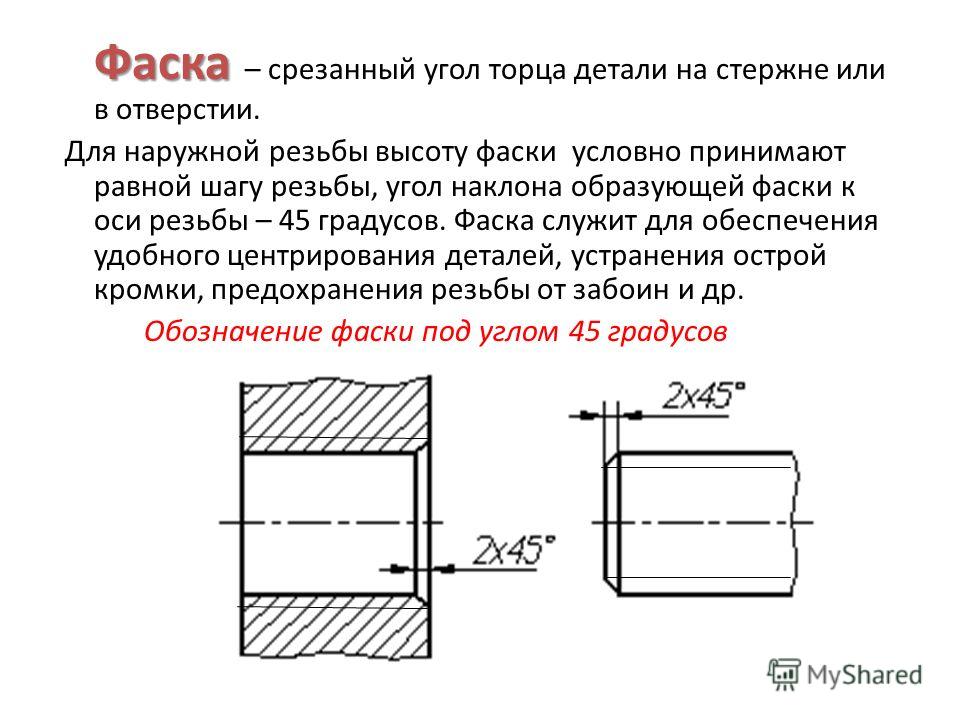 Просто введите имя повторно, и оно снова появится.
Просто введите имя повторно, и оно снова появится.Уголки стальные равнополочные
Размеры и статические параметры уголков стальных равнополочных – британские единицы.
Рекламные ссылки
Свойства в имперских единицах стальных уголков с равными сторонами указаны ниже.
- Steel Angles – Equal Legs – Metric Units
| Size (in x in) | Dimensions | Static Parameters | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Depth – h – (in) | Толщина – s – (дюймы) | Площадь сечения (in 2 ) | Weight (lb f /ft) | Moment of Inertia – I x – (in 4 ) | ||||||||||||
| 12 x 12 | 12 | 1 3/8 | 30. 9 9 | 105 | 410.0 | |||||||||||
| 12 | 1 1/4 | 28.3 | 96.4 | 377.5 | ||||||||||||
| 12 | 1 1/8 | 25.6 | 87.2 | 344.1 | ||||||||||||
| 12 | 1 | 22.9 | 77.8 | 310.4 | ||||||||||||
| 10 x 10 | 10 | 1 3/8 | 25.6 | 87.1 | 232.1 | |||||||||||
| 10 | 1 1/4 | 23.5 | 79.9 | 215.1 | ||||||||||||
| 10 | 1 1/8 | 21.2 | 72.3 | 196.2 | ||||||||||||
| 10 | 1 | 19.0 | 64.7 | 177.3 | ||||||||||||
| 10 | 7/8 | 16.7 | 56.9 | 157.6 | ||||||||||||
| 10 | 3 /4 | 14.4 | 49.1 | 137.2 | ||||||||||||
| 8 x 8 | 8 | 1 1/8 | 16.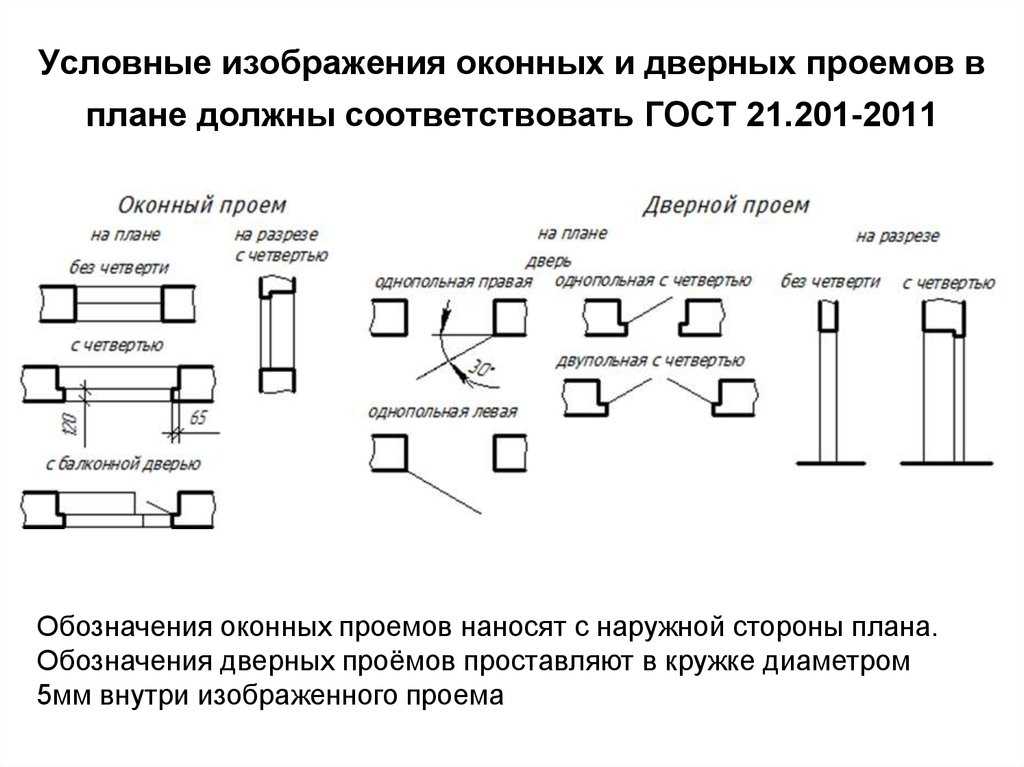 7 7 | 56.9 | 98.0 | |||||||||||
| 8 | 1 | 15.0 | 51.0 | 89.0 | ||||||||||||
| 8 | 7/8 | 13.2 | 45.0 | 79.6 | ||||||||||||
| 8 | 3/4 | 11.4 | 38.9 | 69.7 | ||||||||||||
| 8 | 5/8 | 9.6 | 32.7 | 59.4 | ||||||||||||
| 8 | 9/16 | 8.7 | 29.6 | 54.1 | ||||||||||||
| 8 | 1/2 | 7.8 | 26.4 | 48.6 | ||||||||||||
| 6 x 6 | 6 | 1 | 11.0 | 37.4 | 35.5 | |||||||||||
| 6 | 7/8 | 9,7 | 33.1 | 31,9 | ||||||||||||
| 6 | 3/4 | 8,4 | 28,7 | 28,2 | 28,7 | 28,2 | 28,7 | 28,2 | 28,7 | 28,2 | 28,7 | 28,4 | 28,7 | 28,4 | 28,7 | .24.2 |
| 6 | 9/16 | 6.4 | 21.9 | 22.1 | ||||||||||||
| 6 | 1/2 | 5.8 | 19.6 | 19.9 | ||||||||||||
| 6 | 7/16 | 5.1 | 17.2 | 17.7 | ||||||||||||
| 6 | 3/8 | 4.4 | 14.9 | 15.4 | ||||||||||||
| 6 | 5/16 | 3.7 | 12.4 | 13.0 | ||||||||||||
| 5 x 5 | 5 | 7/8 | 8.0 | 27.2 | 17.8 | |||||||||||
| 5 | 3/4 | 6.9 | 23.6 | 15.7 | ||||||||||||
| 5 | 5/8 | 5.9 | 20.0 | 13.6 | ||||||||||||
| 5 | 1/2 | 4.8 | 16.2 | 11.3 | ||||||||||||
| 5 | 7/16 | 4. 2 2 | 14.3 | 10.0 | ||||||||||||
| 5 | 3/8 | 3.6 | 12.3 | 8.74 | ||||||||||||
| 5 | 5/16 | 3.0 | 10.3 | 7.42 | ||||||||||||
| 4 x 4 | 4 | 3/4 | 5.4 | 18.5 | 7.67 | |||||||||||
| 4 | 5/8 | 4.6 | 15.7 | 6.66 | ||||||||||||
| 4 | 1/2 | 3.8 | 12.8 | 5.56 | ||||||||||||
| 4 | 7/16 | 3.3 | 11.3 | 4.97 | ||||||||||||
| 4 | 3/ 8 | 2.9 | 9.8 | 4.36 | ||||||||||||
| 4 | 5/16 | 2.4 | 8.2 | 3.71 | ||||||||||||
| 4 | 1/4 | 1.9 | 6.6 | 3.04 | ||||||||||||
| 3 1/2 x 3 1/2 | 3 1/2 | 1/2 | 3.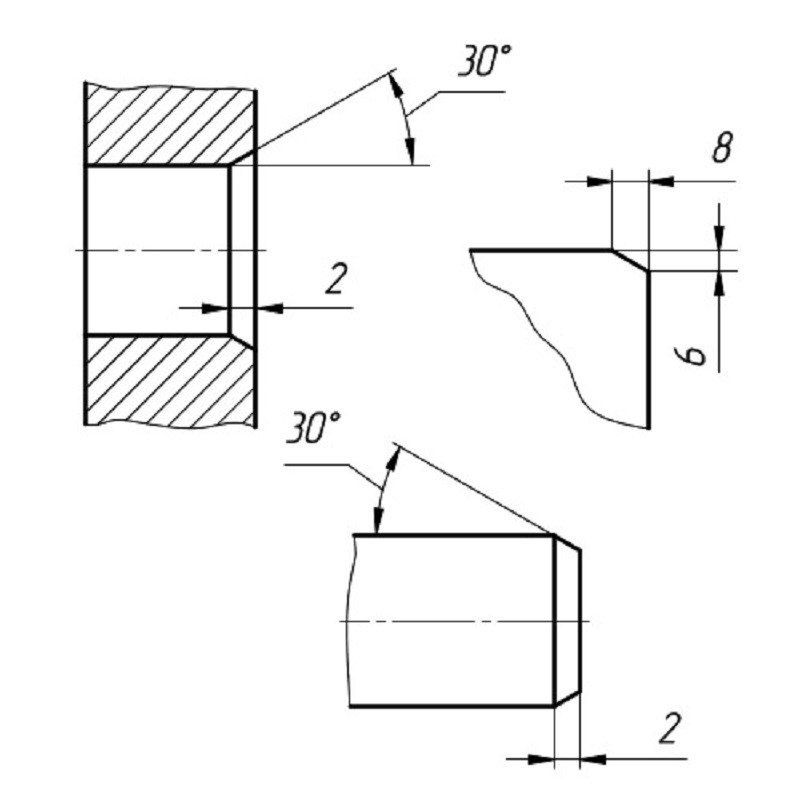 3 3 | 11.1 | 3.64 | |||||||||||
| 3 1/2 | 7 /16 | 2.9 | 9.8 | 3.26 | ||||||||||||
| 3 1/2 | 3/8 | 2.5 | 8.5 | 2.87 | ||||||||||||
| 3 1/2 | 5/16 | 2.1 | 7,2 | 2,45 | ||||||||||||
| 3 1/2 | 1/4 | 1.7 | 5.8 | 2.01 | ||||||||||||
| 3 x 3 | 3 | 1/2 | 2.75 | 9.4 | 2.22 | |||||||||||
| 3 | 7/16 | 2.43 | 8.3 | 1.99 | ||||||||||||
| 3 | 3/8 | 2.11 | 7.2 | 1.76 | ||||||||||||
| 3 | 5/16 | 1.78 | 6.1 | 1.51 | ||||||||||||
| 3 | 1/4 | 1.44 | 4.9 | 1.24 | ||||||||||||
| 3 | 3/16 | 1. 09 09 | 3.7 | 0.96 | ||||||||||||
| 2 1/ 2 x 2 1/2 | 2 1/2 | 1/2 | 2.25 | 7.7 | 1.23 | |||||||||||
| 2 1/2 | 3/8 | 1.73 | 5.9 | 0.98 | ||||||||||||
| 2 1/2 | 5/16 | 1.46 | 5.0 | 0.85 | ||||||||||||
| 2 1/2 | 1/4 | 1.19 | 4.1 | 0.70 | ||||||||||||
| 2 1/2 | 3/16 | 0.90 | 3.1 | 0.55 | ||||||||||||
| 2 x 2 | 2 | 3/8 | 1.36 | 4.7 | 0.48 | |||||||||||
| 2 | 5/16 | 1.15 | 3.9 | 0.42 | ||||||||||||
| 2 | 1/4 | 0.94 | 3.2 | 0.35 | ||||||||||||
| 2 | 3/16 | 0.72 | 2.4 | 0. 27 27 | ||||||||||||
| 2 | 1/8 | 0.48 | 1.7 | 0.19 | ||||||||||||
- 1 in = 25.4 mm
- 1 cm 4 = 10 -8 m = 10 4 mm
- 1 В 4 = 4,16×10 5 мм 4 = 41,6 см 4
- 1 см 3 = 10 -6
- 1 см 3 = 10 -6
- 1 см 3 = 10 -6
- 1 3 . 3
- 1 см 3 = 10 -6
Стандартный метод указания угла: L 2 x 2 x 1/4 – указывает угол 2 дюйма в глубину и ширину – и 1/4 дюйма в толщину.
Рекламные ссылки
Связанные темы
Связанные документы
Engineering ToolBox — Расширение SketchUp — 3D-моделирование онлайн!
Добавляйте стандартные и настраиваемые параметрические компоненты, такие как балки с полками, пиломатериалы, трубопроводы, лестницы и т. д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, увлекательными и бесплатными программами SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!
д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, увлекательными и бесплатными программами SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!
Перевести
О Инженерном наборе инструментов!
Мы не собираем информацию от наших пользователей. В нашем архиве сохраняются только электронные письма и ответы. Файлы cookie используются только в браузере для улучшения взаимодействия с пользователем.
Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложений на локальном компьютере. Эти приложения будут — из-за ограничений браузера — отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные.
Google использует файлы cookie для показа нашей рекламы и обработки статистики посетителей. Пожалуйста, прочитайте Конфиденциальность и условия Google для получения дополнительной информации о том, как вы можете контролировать показ рекламы и собираемую информацию.

 Линии могут быть как параллельными, так и непараллельными.
Линии могут быть как параллельными, так и непараллельными.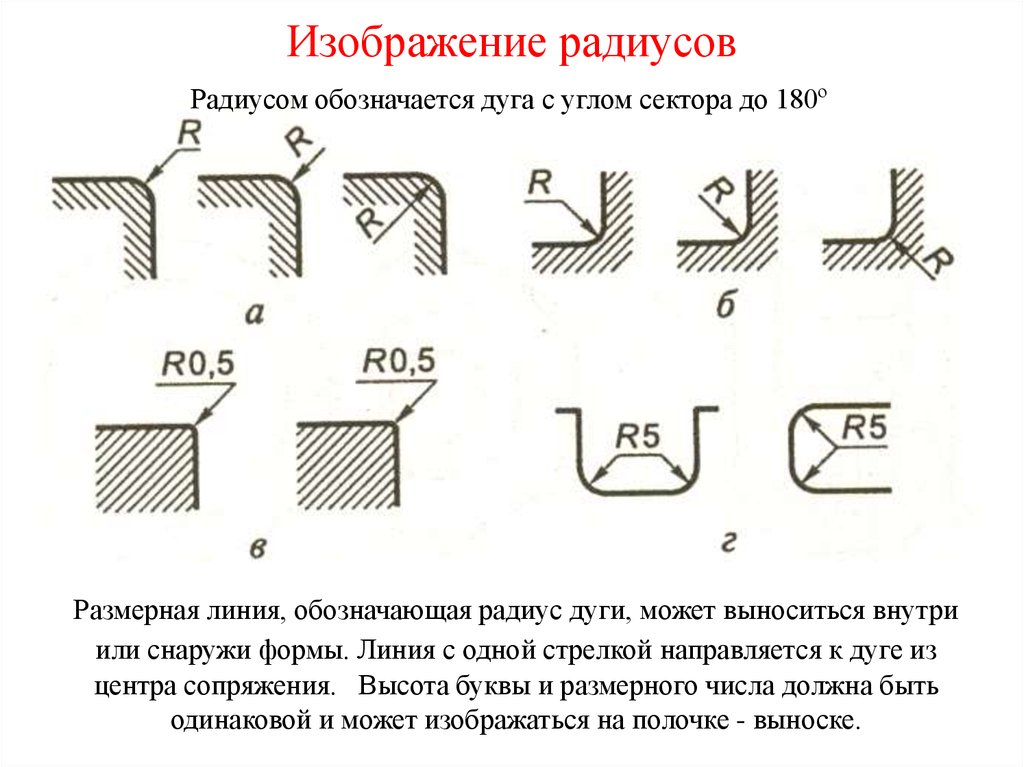
 0148 24.2
0148 24.2