Обозначение радиуса на чертеже гост: ГОСТ 2.307-68* «ЕСКД. Нанесение размеров и предельных отклонений»

ГОСТ 2.307-68*. ЕСКД. Нанесение размеров и предельных отклонений (46967)

---

Черт. 28

2.24. При нанесении размера диаметра внутри окружности размерные числа смещают относительно середины размерных линий.

2.25. При нанесении нескольких параллельных или концентричных размерных линий на небольшом расстоянии друг от друга размерные числа над ними рекомендуется располагать в шахматном порядке (черт. 29).

Черт. 29

2.26. Размерные числа линейных размеров при различных наклонах размерных линий располагают, как показано на черт 30.

Черт. 30

Если необходимо нанести размер в заштрихованной зоне, соответствующее размерное число наносят на полке линии-выноски (черт. 31).

Черт. 31

2.27. Угловые размеры наносят так, как показано на черт. 32. В зоне, расположенной выше горизонтальной осевой линии, размерные числа помещают над размерными линиями со стороны их выпуклости; в зоне, расположенной ниже горизонтальной осевой линии – со стороны вогнутости размерных линий. В заштрихованной зоне наносить размерные числа не рекомендуется. В этом случае размерные числа указывают на горизонтально нанесенных полках.

Черт. 32

Для углов малых размеров при недостатке места размерные числа помещают на полках линий-выносок в любой зоне (черт. 33).

Черт. 33

2.28. На строительных чертежах допускается линейные и угловые размерные числа и надписи наносить без полок линий выносок.

2.29. Если для написания размерного числа недостаточно места над размерной линией, то размеры наносят, как показано на черт. 34; если недостаточно места для нанесения стрелок, то их наносят, как показано на черт. 35.

Черт. 34

Черт. 36

Способ нанесения размерного числа при различных положениях размерных линий (стрелок) на чертеже определяется наибольшим удобством чтения.

2.30. Размерные числа и предельные отклонения не допускается разделять или пересекать какими бы то ни было линиями чертежа. Не допускается разрывать линию контура для нанесения размерного числа и наносить размерные числа в местах пересечения размерных, осевых или центровых линий.

В месте нанесения размерного числа осевые, центровые линии и линии штриховки прерывают (черт. 36 и 37).

Черт. 36

Черт. 37

2.29, 2.30. (Измененная редакция, Изм. № 2).

2.31. Размеры, относящиеся к одному и тому же конструкционному элементу (пазу, выступу, отверстию и т. п.), рекомендуется группировать в одном месте, располагая их на том изображении, на котором геометрическая форма данного элемента показана наиболее полно (черт. 38).

Черт. 38

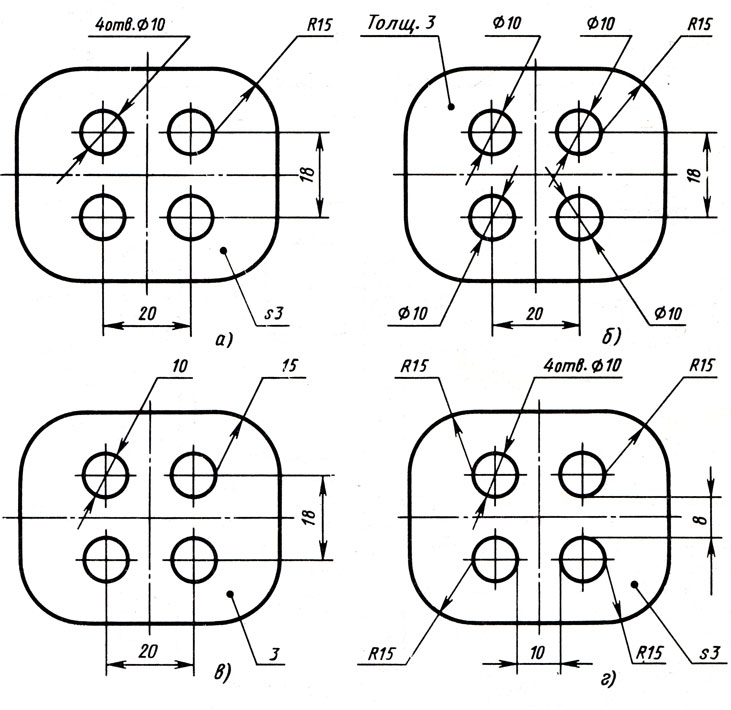
2.32. При нанесении размера радиуса перед размерным числом помещают прописную букву R.

2.33. Если при нанесении размера радиуса дуги окружности необходимо указать размер, определяющий положение ее центра, то последний изображают в виде пересечения центровых или выносных линий.

При большой величине радиуса центр допускается приближать к дуге, в этом случае размерную линию радиуса показывают с изломом под углом 90 ° (черт. 39).

Черт. 39

2.34. Если не требуется указывать размеры, определяющие положение центра дуги окружности, то размерную линию радиуса допускается не доводить до центра и смещать ее относительно центра (черт. 40).

Черт. 40

2.35. При проведении нескольких радиусов из одного центра размерные линии любых двух радиусов не располагают на одной прямой (черт. 41).

черт. 41

При совпадении центров нескольких радиусов их размерные линии допускается не доводить до центра, кроме крайних (черт. 41а).

Черт. 41a

2.36. Размеры радиусов наружных округлении наносят, как показано на черт. 42, внутренних скруглений – на черт. 43.

Черт. 42

Черт. 43

Радиусы скругления, размер которых в масштабе чертежа 1 мм и менее, на чертеже не изображают и размеры их наносят, как показано на черт. 43а.

Черт. 43а

Способ нанесения размерных чисел при различных положениях размерных линий (стрелок) на чертеже определяется наибольшим удобством чтения. Размеры одинаковых радиусов допускается указывать на общей полке, как показано на черт. 43б:

Черт. 43б

Если радиусы скруглений, сгибов и т. п. на всем чертеже одинаковы или какой-либо радиус является преобладающим, то вместо нанесения размеров этих радиусов непосредственно на изображении рекомендуется в технических требованиях делать запись типа: «Радиусы скруглений 4 мм»; «Внутренние радиусы сгибов 10 мм»; «Неуказанные радиусы 8 мм» и т.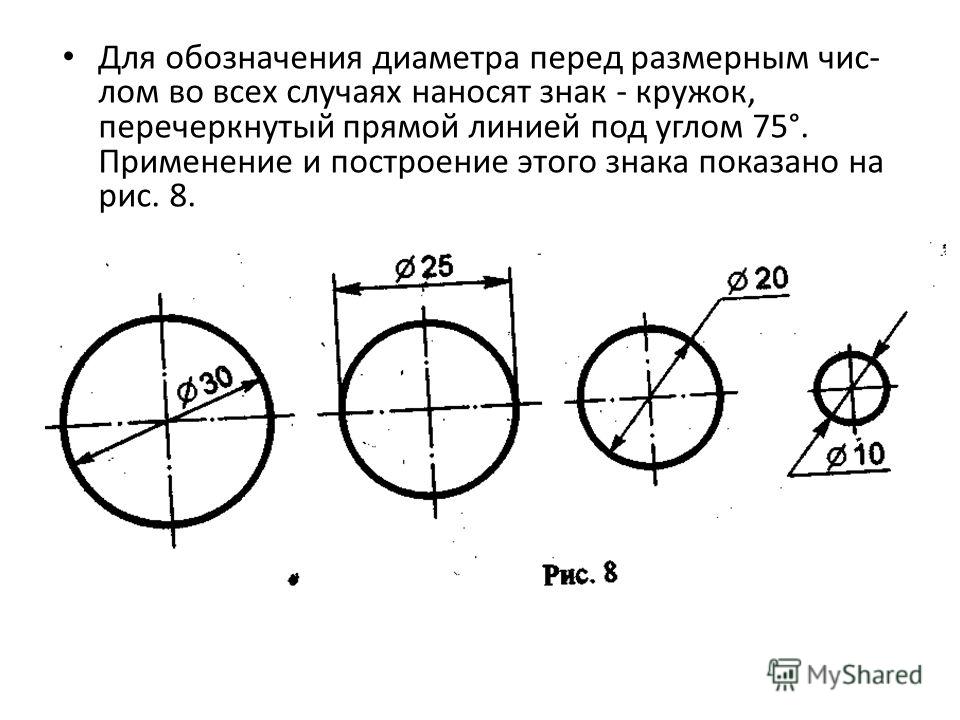 п.

2.35, 2.36. (Измененная редакция, Изм. № 2).

2.37. При указании размера диаметра (во всех случаях) перед размерным числом наносят знак «??».

2.38. Перед размерным числом диаметра (радиуса) сферы также наносят знак Æ (R) без надписи «Сфера» (черт. 44). Если на чертеже трудно отличить сферу от других поверхностей, то перед размерным числом диаметра (радиуса) допускается наносить слово «Сфера» или знак О, например, «Сфера 18, ОR12».

Диаметр знака сферы равен размеру размерных чисел на чертеже.

Черт. 44

2.39. Размеры квадрата наносят, как показано на черт. 45, 46 и 46а.

Черт. 45

Черт. 46

Черт. 46а

Высота знака □ должна быть равна высоте размерных чисел на чертеже.

2.38, 2.39 (Измененная редакция, Изм. № 2).

2.40. Перед размерным числом, характеризующим конусность, наносят знак «??», острый угол которого должен быть направлен в сторону вершины конуса (черт. 47).

Черт. 47

Знак конуса и конусность в виде соотношения следует наносить над осевой линией или на полке линии-выноски.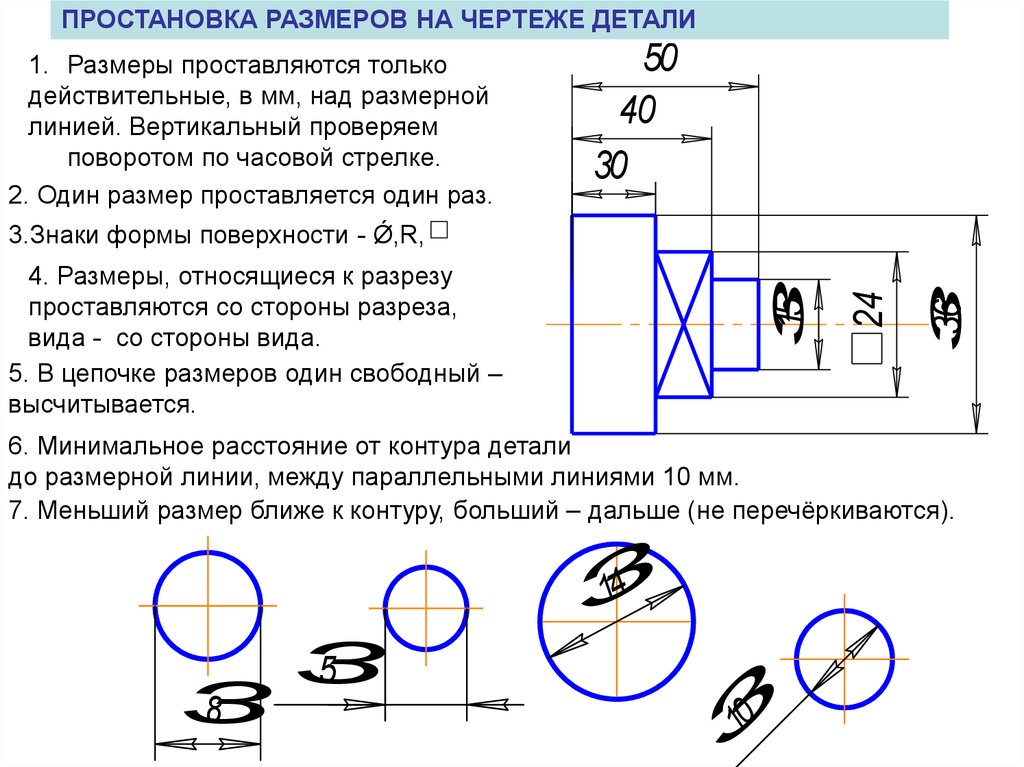

2.41. Уклон поверхности следует указывать непосредственно у изображения поверхности уклона или на полке линии-выноски в виде соотношения (черт. 48а), в процентах (черт. 48б) или в промиллях (черт. 48в). Перед размерным числом, определяющим уклон, наносят знак «», острый угол которого должен быть направлен в сторону уклона.

Черт. 48

2.42. Отметки уровней (высоты, глубины) конструкции или ее элемента от какого-либо отсчетного уровня, принимаемого за «нулевой» на виде и разрезе, помещают на выносных линиях (или на линиях контура) и обозначают знаком «  », выполненным сплошными тонкими линиями, длина штрихов 2 – 4 мм под углом 45° к выносной линии или линии контура (черт. 49а), на виде сверху их следует наносить в рамке непосредственно на изображении или на линии-выноске (черт. 49б), или как показано на черт. 49а.

Черт. 49

Отметки уровней указывают в метрах с точностью до третьего десятичного знака без обозначения единицы измерения.

2.43. Размеры фасок под углом 45° наносят, как показано на черт.

50.

Черт. 50

Допускается указывать размеры не изображенной на чертеже фаски под углом 45°, размер которой в масштабе чертежа 1 мм и менее, на полке линии-выноски, проведенной от грани (черт. 50а).

Черт. 50а

Размеры фасок под другими углами указывают по общим правилам – линейным и угловым размерами (черт. 51а и б) или двумя линейными размерами (черт. 51в).

Черт. 51

2.40-2.43. (Измененная редакция, Изм. № 2).

2.44. Размеры нескольких одинаковых элементов изделия, как правило, наносят один раз с указанием на полке линии-выноски количества этих элементов (черт. 52а).

Допускается указывать количество элементов, как показано на черт. 52б.

Черт. 52

2.45. При нанесении размеров элементов, равномерно расположенных по окружности изделия (например, отверстий), вместо угловых размеров, определяющих взаимное расположение элементов, указывают только их количество (черт. 53-55).

Черт. 53

Черт. 54

Черт. 55

2.46. Размеры двух симметрично расположенных элементов изделия (кроме отверстий) наносят один раз без указания их количества, группируя, как правило, в одном месте все размеры (черт. 56 и 57).

Черт. 56

___________

* Размеры для справок.

Черт. 57

Количество одинаковых отверстий всегда указывают полностью, а их размеры – только один раз.

(Измененная редакция, Изм. № 2).

2.47. При нанесении размеров, определяющих расстояние между равномерно расположенными одинаковыми элементами изделия (например, отверстиями), рекомендуется вместо размерных цепей наносить размер между соседними элементами и размер между крайними элементами в виде произведения количества промежутков между элементами на размер промежутка (черт. 58).

Черт. 58

2.47а. Допускается не наносить на чертеже размеры радиуса дуги окружности сопрягающихся параллельных линий (черт. 58а).

Черт. 58 a

(Введен дополнительно, Изм. № 2).

2.48. При большом количестве размеров, нанесенных от общей базы, допускается наносить линейные и угловые размеры, как показано на черт. 59 и 60, при этом проводят общую размерную линию от отметки «0» и размерные числа наносят в направлении выносных линий у их концов.

Черт. 59

Черт. 60

2.48а. Размеры диаметров цилиндрического изделия сложной конфигурации допускается наносить, как показано на черт. 60а.

Черт. 60а

(Введен дополнительно, Изм. № 2).

2.49. При большом количестве однотипных элементов изделия, неравномерно расположенных на поверхности, допускается указывать их размеры в сводной таблице, при этом применяется координатный способ нанесения отверстий с обозначением их арабскими цифрами (черт. 61), или обозначение однотипных элементов прописными буквами (черт. 61а).

Черт. 61

Черт. 61a

Обозначение отверстий	Кол.	Размер, мм
А	2	3
Б	4	6,5

2.50. Одинаковые элементы, расположенные в разных частях изделия (например, отверстия), рассматривают как один элемент, если между ними нет промежутка (черт.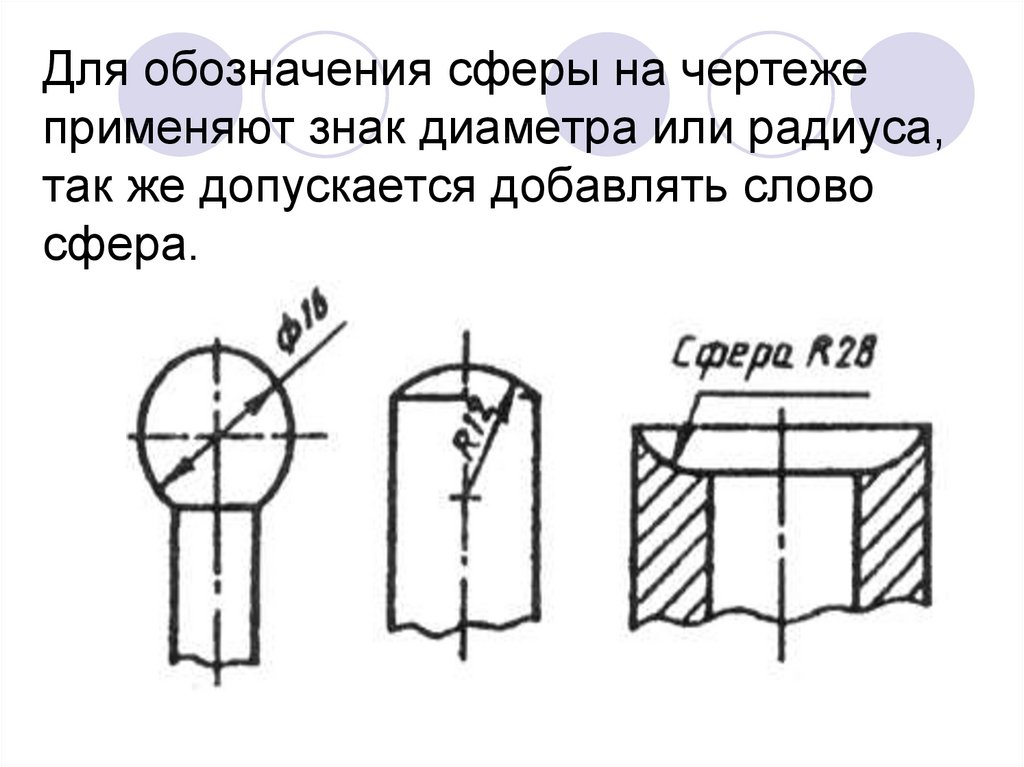 62а) или если эти элементы соединены тонкими сплошными линиями (черт. 62б).

При отсутствии этих условий указывают полное количество элементов (черт. 62в).

Черт. 62

2.51. Если одинаковые элементы изделия (например, отверстия) расположены на разных поверхностях и показаны на разных изображениях, то количество этих элементов записывают отдельно для каждой поверхности (черт. 63).

Черт. 63

Допускается повторять размеры одинаковых элементов изделия или их групп (в том числе отверстии), лежащих на одной поверхности, только в том случае, когда они значительно удалены друг от друга и не увязаны между собой размерами (черт. 64 и 65).

Черт. 64

Черт. 65

2.49-2.51. (Измененная редакция, Изм. № 2).

2.52. Если на чертеже показано несколько групп близких по размерам отверстий, то рекомендуется отмечать одинаковые отверстия одним из условных знаков, приведенных на черт. 66. Допускается применять и другие условные знаки.

Черт. 66

Отверстия обозначают условными знаками на том изображении, на котором указаны размеры, определяющие положение этих отверстий.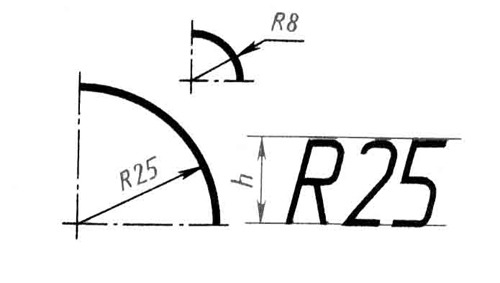

На строительных чертежах допускается одинаковые группы отверстий обводить сплошной тонкой линией с поясняющей надписью.

2.53 При обозначении одинаковых отверстий условными знаками количество отверстий и их размеры допускается указывать в таблице (черт. 67).

Черт. 67

(Измененная редакция, Изм. № 2).

2.54. При изображении детали в одной проекции размер ее толщины или длины наносят, как показано на черт. 68.

Черт. 68

2.55. Размеры детали или отверстия прямоугольного сечения могут быть указаны на полке линии-выноски размерами сторон через знак умножения. При этом на первом месте должен быть указан размер той стороны прямоугольника, от которой проводится линия-выноска (черт. 68а).

Черт. 68а

(Измененная редакция, Изм. № 2).

3. НАНЕСЕНИЕ ПРЕДЕЛЬНЫХ ОТКЛОНЕНИЙ РАЗМЕРОВ

3.1. Предельные отклонения размеров следует указывать непосредственно после номинальных размеров. Предельные отклонения линейных н угловых размеров относительно низкой точности допускается не указывать непосредственно после номинальных размеров, а оговаривать общей записью в технических требованиях чертежа при условии, что эта запись однозначно определяет значения и знаки предельных отклонений.

Общая запись о предельных отклонениях размеров с неуказанными допусками должна содержать условные обозначения предельных отклонений линейных размеров в соответствии с ГОСТ 25346-89 (для отклонений по квалитетам) или по ГОСТ 25670-83 (для отклонений, по классам точности). Симметричные предельные отклонения, назначаемые по квалитетам, следует обозначать  с указанием номера квалитета.

Обозначения односторонних предельных отклонений по квалитетам, назначаемых только для круглых отверстий и валов (вариант 4 по ГОСТ 25670-83) дополняются знаком диаметра (??).

Примеры общих записей, соответствующие вариантам по ГОСТ 25670-83 для 14 квалитета и (или) класса точности «средний», приведены в табл. 1:

Таблица 1

Номер варианта	Пример записи условными обозначениями
1.	Н14, h24,  или Н14, h24,
2.	+t2, -t2,
3.	или
4.	Н14, ??h24,  или Н14, ??h24,

Примечания:

1. Допускается записи о неуказанных предельных отклонениях размеров дополнять поясняющими словами, например, «Неуказанные предельные отклонения размеров: Н14, h24, ».

2. Если технические требования па чертеже состоят из одного пункта, содержащего запись о неуказанных предельных отклонениях размеров, или эта запись приводится в текстовых документах, то она должна обязательно сопровождаться поясняющими словами, например, «Неуказанные предельные отклонения размеров ».

(Измененная редакция, Изм. № 2).

3.la. Неуказанные предельные отклонения радиусов закруглении, фасок и углов не оговариваются отдельно, а должны соответствовать приведенным в ГОСТ 25670-83 в соответствии с квалитетом или классом точности неуказанных предельных отклонений линейных размеров.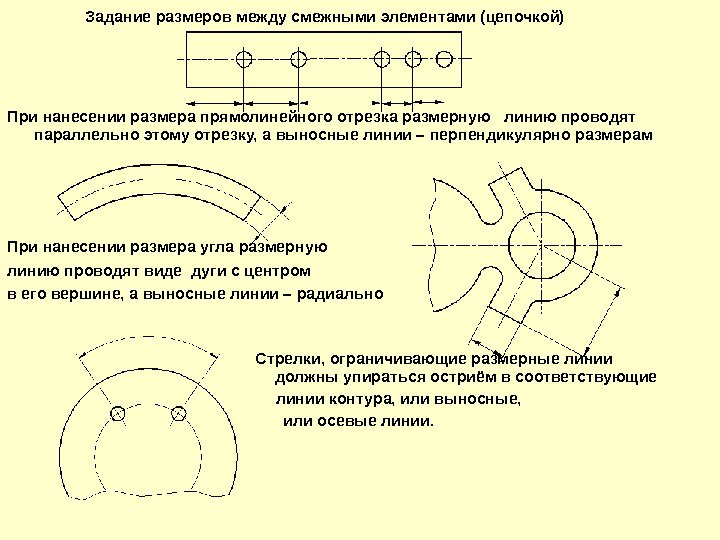

Если все предельные отклонения линейных размеров указаны непосредственно после номинальных размеров (общая запись отсутствует), то неуказанные предельные отклонения радиусов закруглений, фасок и углов должны соответствовать приведенным в ГОСТ 25670-83 для квалитетов от 12 до 16 и на чертеже не оговариваются.

Скачать бесплатно

Графические работы по инженерной графике. Нанесение размеров на чертеже.

Практические задания по инженерной графике



По изображениям изделия или предмета на чертеже получают информацию не только о его форме, но и о его размерах, а также размерах его отдельных элементов. С этой целью на чертежах обозначения в виде размерных чисел, независимо от того, в каком масштабе и с какой точностью выполнены изображения.
Правила нанесения размеров на чертежах установлены ГОСТ 2.307—68.

Размеры на чертеже указывают размерными числами, размерными и выносными линиями. Размерные числа линейных величин на чертежах, как правило, указывают в миллиметрах без указания единиц измерения. В тех случаях, когда необходимо применять другие единицы измерения длины, их показывают после размерного числа.
Угловые величины, как правило, указывают в градусах, минутах, секундах. Другие единицы измерения размеров (линейных и угловых) на чертежах могут применяться лишь в порядке исключения.

Размерные числа наносят над размерной линией (размерной полкой), по возможности ближе к ее середине. Зазор между размерным числом и размерной линией должен быть около 1,0 мм.
Высоту цифр размерных чисел принимают не менее 3,5 мм.
Высота размерных цифр, как и букв на чертежах регламентируется ГОСТ 2.304-81.

Размерная линия выполняется сплошной тонкой линией чертежа и проводится параллельно отрезку, размер которого над ней наносится (рис. 1). Ее проводят между выносными линиями, проведенными перпендикулярно размерным линиям (размерным полкам). Допускается размерные линии проводить непосредственно к линиям видимого контура, осевым и центровым. В отдельных случаях размерная линия может проводиться не перпендикулярно выносной линии.

Размерные линии ограничивают стрелки. В отдельных случаях их проводят не полностью, а с обрывом стрелки с одной стороны. Размер стрелки выбирают в зависимости от принятой на чертеже толщины сплошной толстой основной линии.
В пределах одного чертежа величина стрелок должна быть по возможности одинаковой. Стрелка не должна иметь слишком широко расставленные лучи (угол между лучами в соответствии со стандартом должен составлять 20 градусов).
Не рекомендуется в качестве размерных линий использовать контурные, осевые, центровые и выносные линии.

Если длина размерной линии мала для размещения стрелок, то размерную линию продолжают за выносные линии, и размеры наносят, как показано на рис. 2, поз. а.

Выносные линии выполняются сплошной тонкой линией чертежа и проводят от границ измерений; они являются вспомогательными и служат для размещения между ними размерных линий.
Выносные линии следует по возможности располагать вне контура изображения, перпендикулярно прямолинейному отрезку, размер которого необходимо указать. Выносные линии должны выходить за концы стрелок размерных линий на 1…5 мм.
Не рекомендуется располагать выносные линии таким образом, чтобы они пересекали размерные полки других элементов, а также выполнять их так, чтобы они, по возможности, не пересекали основные линии чертежа (линии видимого контура изображаемого изделия).

Минимальное расстояние от размерной линии до параллельной ей линии, размер которой она указывает, должно быть 10 мм, а между несколькими параллельными размерными линиями — 7 мм.

Угловые размеры на чертежах проставляются в градусах, минутах и секундах с указанием единиц измерения. Размер угла наносят над размерной линией, которая проводится в виде дуги с центром в вершине угла. Выносные линии в этом случае проводятся радиально (рис. 2, поз. б).

***



При различных наклонах размерных линий размерные числа линейных и угловых размеров располагают так, чтобы надписи находились в наиболее удобном для чтения положении.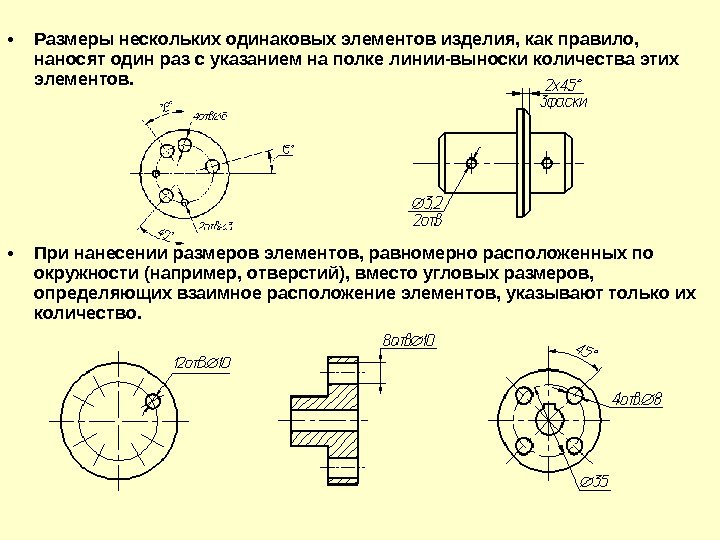 Если размерная линия будет находиться в зоне, которая на чертеже заштрихована, размерные числа наносят на полках линий-выносок.

Если для написания размерного числа мало места над размерной линией или это место занято другими элементами изображения и вписать в него размерное число невозможно, размерное число наносят по одному из вариантов, приведенных на рис. 3.

С целью упрощения ряда изображений, а также удобства чтения чертежа, стандарт предусматривает применение условных обозначений в виде букв латинского алфавита и графических знаков, которые ставятся перед размерными числами. На чертежах применяются знаки и буквы для обозначения диаметра и радиуса, длины дуги и квадрата, уклона и конусности, сферы, толщины и длины детали.

Перед размерным числом диаметра наносится знак Ø. Причем между знаком и числом никаких пропусков не предусмотрено. Для окружностей малого диаметра размерные линии стрелки и сам размер наносят на выносных полках.

Перед размерным числом радиуса дуги или окружности должен ставится знак в виде прописной латинской буквы R. Размерную линию в этом случае проводят по направлению к центру дуги и ограничивают только одной стрелкой, упирающейся в дугу или ее продолжение.
Если величина радиуса на чертеже менее 6 мм, стрелку рекомендуется располагать с внешней стороны дуги. При необходимости задания положения центра дуги его отмечают пересечением центровых или выносных линий.

Если на виде изделия присутствует несколько окружностей или дуг одинакового диаметра, то указывается диаметр (радиус) лишь одного элемента (окружности, дуги), при этом на размерной или выносной полке указывается количество одинаковых элементов, например: 3 отв. Ø5

В тех случаях, когда на чертеже изображена дуга большого радиуса, для которой центр можно не обозначать, размерную линию обрывают, не доводя до центра. Если же в этом случае центр необходимо отметить, допускается приближать его к дуге. Размерная линия в этом случае показывается с изломом 90°, и оба участка размерной линии проводятся параллельно.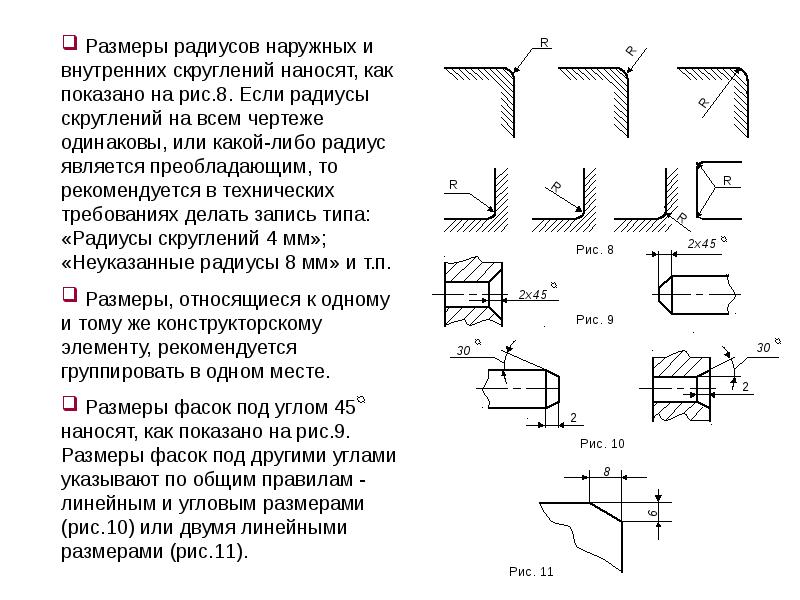
Не следует располагать на одной прямой размерные линии, выходящие из одного центра и предназначенные для обозначения размерных дуг. Радиусами рекомендуется обозначать дуги до 180°; дуги, величина которых составляет более 180°, обозначаются диаметром.

Знак дуги наносится над размерным числом. Длину дуги задают в линейных единицах, а размерное число, обозначающее дугу, наносится над размерной линией в соответствии с обычными требованиями.

Для простановки размеров квадрата применяют соответствующий знак в виде квадрата, высота которого равна 7/10 высоты размерного числа. При ином расположении квадрата наносят размеры его сторон. Следует отметить, что знак квадрата наносят только на том изображении, на котором он проецируется в линию (рис. 4).

Знак конусности поверхности наносится на полке линии-выноски, расположенной параллельно оси конуса или на оси конуса (рис. 6). Знак конусности располагают так, чтобы его острый угол был направлен в сторону вершины конуса.
Величину конусности определяют отношением разности диаметров двух поперечных сечений конуса к расстоянию между этими сечениями:

k = (D — d)/l,

где D — диаметр большого сечения; d — диаметр меньшего сечения; l — расстояние между сечениями. Конусность указывают в виде простого дробного числа.

Знак уклона прямой указывают на полке линии-выноски (рис. 7). Уклон i представляет собой тангенс угла между данной прямой и горизонтальной или вертикальной прямой.
Знак уклона располагается так, чтобы острый угол его был направлен в сторону уклона прямой. Уклон, как и конусность, на чертеже задают простой дробью, в процентах или в промилях.

Для обозначения сферы на чертеже применяют знак диаметра или радиуса. В тех случаях, когда по чертежу сферу трудно отличить от других поверхностей, перед знаком радиуса или диаметра допускается добавлять слово «Сфера». Надпись на чертеже выполняется по типу «Сфера Ø17» или «Сфера R10».

Простые плоские детали (пластины, прокладки и т. п.) изображаются в виде одной проекции. В этих случаях ее толщину обозначают строчной буквой s, т. е.надпись на чертеже выполняется по типу s2 и располагается на полке линии-выноски.
Длину предмета указывают буквой l.

Фаски на чертежах наносят двумя линейными размерами или одним линейным и одним угловым. В том случае, если угол наклона образующей конуса равен 45°, применяют упрощенное обозначение фаски, когда размерная линия проводится параллельно оси конуса, а надпись выполняется по типу «2 х 45˚».

При нанесении размеров на чертежах следует учитывать, что дважды один и тот же размер изделия на чертежах не указывается (например, на разных видах) – каждый размер необходимо указать лишь один раз. При выполнении практических заданий следует, также, внимательно изучить чертеж, чтобы проставить все необходимые размеры, по которым можно было бы изготовить вычерчиваемое изделие.

В качесте закрепления практических навыков нанесения размеров на чертежах предлагается к выполнению работа, в которой обучающийся должен начертить изображение тонкого изделия (прокладка или пластина), и проставить на чертеже все необходимые размеры.

Скачать образец работы для последующей печати и использования в качестве раздаточного материала можно здесь.

***

Графическая работа №3.
Построение сопряжений на чертежах.



Главная страница

• Страничка абитуриента

Дистанционное образование

• Группа ТО-81
• Группа М-81
• Группа ТО-71
  

Специальности

• Ветеринария
• Механизация сельского хозяйства
• Коммерция
• Техническое обслуживание и ремонт автотранспорта

Учебные дисциплины

• Инженерная графика
• МДК. 01.01. «Устройство автомобилей»
•    Карта раздела
•       Общее устройство автомобиля
•       Автомобильный двигатель
•       Трансмиссия автомобиля
•       Рулевое управление
•       Тормозная система
•       Подвеска
•       Колеса
•       Кузов
•       Электрооборудование автомобиля
•       Основы теории автомобиля
•       Основы технической диагностики
• Основы гидравлики и теплотехники
• Метрология и стандартизация
• Сельскохозяйственные машины
• Основы агрономии
• Перевозка опасных грузов
• Материаловедение
• Менеджмент
• Техническая механика
• Советы дипломнику

Олимпиады и тесты

• «Инженерная графика»
• «Техническая механика»
• «Двигатель и его системы»
• «Шасси автомобиля»
• «Электрооборудование автомобиля»

Диаметр, радиус и длина окружности (видео и практика)

СтенограммаЧасто задаваемые вопросыПрактика

Привет, ребята! Добро пожаловать в это видео о радиусе, диаметре и длине окружности.

Круги существуют столько же, сколько существует Земля. Люди могли видеть естественные круги, наблюдая за луной, солнцем и другими различными природными круглыми формами.

Первое технологическое изобретение с использованием круглой формы, однако, не было до 3500 г. до н.э., и это было изобретение гончарного круга. Затем, 300 лет спустя, их использовали для колес колесниц. Когда люди начали видеть ценность и использование объектов круглой формы, они начали изучать круги.

Такие термины, как радиус , диаметр и окружность , помогают нам отслеживать различные измерения окружности.

Итак, теперь давайте посмотрим, что представляет собой каждое из этих измерений.

Определения

Середина окружности

Во-первых, давайте определим середину , чтобы вы поняли, о чем я говорю, когда я на нее ссылаюсь. Вот круг:

Середина — это точный центр круга, где находится точка.

Теперь давайте посмотрим на другие термины.

Радиус круга

Радиус — это длина от середины круга до внешнего края круга. Радиус обозначается строчной буквой \(r\).

Диаметр круга

Диаметр — это полная длина круга, проходящая от края через середину до другой стороны. То есть вся эта длина прямо здесь. Диаметр круга обозначается буквой \(d\).

Окружность круга

Окружность — это расстояние вокруг внешнего края этого круга. Окружность обозначается заглавной буквой \(C\).

Окружность сравнима с периметром фигуры, такой как параллелограмм . Если бы вы разрезали линию круга, как если бы это была нить, и выложили ее по размеру. Эта длина будет эквивалентна окружности. Однако, поскольку круг имеет непрерывную кривую, мы используем слово окружность , а не периметр , чтобы отличить его.

Теперь, когда мы рассмотрели, что такое радиус, диаметр и длина окружности, давайте посмотрим, как их рассчитать.

Расчеты

Если бы кто-то просто вручил вам лист бумаги с кружком на нем…. Ну, на самом деле, это было бы довольно странно.

Но допустим, мы хотим найти радиус, диаметр и длину окружности этого круга, и все, что у нас есть, это линейка.

Для начала проще всего взять линейку и измерить от самого центра круга расстояние между внешним краем. Это будет диаметр.

Допустим, что когда мы измерили, мы получили длину 9 см для диаметра.

Ну, мы знаем, что если наш радиус проходит от середины до внешнего края, то все, что нам нужно сделать, чтобы найти длину нашего радиуса, это разделить длину диаметра на 2.

Итак, когда мы берем 9 и делим на 2 получаем длину радиуса 4,5см.

Формула радиуса

Формула радиуса может быть записана как \(r=\frac{d}{2}\)

Формула диаметра

Формула диаметра может быть записана как \(d=2r\)

Формула длины окружности

Формула длины окружности: \(C=\pi \times d\), или ее можно записать как \(C=2\times \pi \times r\). Любой работает!

Теперь вы можете спросить: «Откуда взялось число пи и почему мы вдруг получаем длину окружности, если умножаем это число пи на наш диаметр? Кто это решил?» Если вы не задаете этот вопрос… Вы должны, и я все равно отвечу на него.

Пи — это символ, который мы используем в математике для обозначения числа 3,14. А на самом деле это просто пи, округленное до сотых. Пи на самом деле не имеет ни конца, ни предсказуемой закономерности. Это просто продолжается.

Однако, когда вы видите символ \(\pi\), обычно (и в нашем случае) будет достаточно 3.14.

Пи — это не случайное число, которое придумали математики и заявили: «Мы каждый раз будем умножать диаметр на число и называть его окружностью». Наоборот, было обнаружено, что пи есть константа 9.0027 отношение между окружностью и диаметром.

Вот почему и как мы получили формулу длины окружности.

Теперь возьмем круг диаметром 9 см и радиусом 4,5 см и рассчитаем длину окружности.

Я собираюсь использовать формулу с диаметром для этого.

Итак, длина окружности равна (я просто перепишу формулу, чтобы помочь нам следить за нашей работой), \(C=\pi \times d\), равно pi, умноженному на диаметр. Итак, теперь все, что нам нужно сделать, это подставить наше число для диаметра. Это равно, а также мы сказали, что пи равно 3,14, \(C=(3,14)(9\text{ см})=28,26\text{ см}\).

А вот и наш ответ! Теперь, чтобы попрактиковаться, попробуйте нарисовать круг на листе бумаги и измерьте его диаметр линейкой. Затем найдите свой радиус и длину окружности.

Надеюсь, это видео было для вас полезным.

Увидимся в следующий раз!

Часто задаваемые вопросы

Q

Каков радиус окружности?

A

Если бы нам нужно было измерить расстояние от центра круга до внешнего края этого круга, мы бы нашли радиус. Подумайте о часах; если бы одна из стрелок была достаточно длинной, чтобы достать до края часов, эту стрелку можно было бы считать радиусом часов – независимо от того, сколько сейчас времени!

Q

Что такое радиус и диаметр?

A

В то время как радиус окружности проходит от центра к краю, диаметр проходит от края к краю и проходит через центр. Диаметр круга по существу делит фигуру пополам. Радиус и диаметр — близкие друзья — радиус круга равен половине длины его диаметра (или: диаметр круга в два раза больше длины его радиуса).

Q

Как называется радиус?

A

Радиус — это отрезок линии. Следовательно, у него есть две конечные точки: точка в центре круга и точка на краю круга, с которым мы его соединили. Имея все это в виду, мы знаем, что называть радиус так же, как и все сегменты линии: имена обеих конечных точек перечислены рядом (часто с чертой над двумя буквами).

Q

Является ли радиус половиной диаметра?

А

Да! Если вы помните только один факт о кругах, пусть это будет он. Просверлите это в своем уме! Радиус равен половине длины диаметра.

Q

Как найти радиус и диаметр?

A

Если мы знаем только радиус круга, мы просто умножим это значение на 2, чтобы получить диаметр \((d=2r)\). Точно так же, если мы знаем только диаметр круга, мы делим его на 2 и получаем радиус \((r=\frac{d}{2})\)!

Но что, если мы не являемся данными ни одним из этих значений? Чтобы определить радиус или диаметр круга, нам нужно знать либо его длину окружности, либо его площадь. 92\)

\(±3=r\)

(Обратите внимание, что квадратный корень из 9 может быть либо 3, либо -3. Поскольку мы имеем дело с реальным кругом, мы будем просто использовать

\( d=2r=6\text{ дюймов}\)

Q

Как рассчитать длину окружности

A

его радиус. Затем мы используем соответствующее значение в этом уравнении: \(C=2πr\) (где « r » представляет радиус, конечно)

Пример. Найдите длину окружности:

\(r=\frac{10\text{ единиц}}{2}=5\text{ единиц}\)

\(C=2πr=2π\times5= 10π\text{ единиц}\)

Q

Почему длина окружности \(2πr\)?

A

Мы знаем, что длина окружности — это длина всего внешнего края круга. (Можно думать об этом так: длина окружности для кругов равна периметру для треугольников, прямоугольников, пятиугольников и т. д.!) Имея это в виду, давайте переставим переменные в уравнении \(C=2πr\), чтобы получить \ (С=2r\timesπ\). Помните, что \(2r=d\) (где d представляет собой диаметр), поэтому мы могли бы переписать это уравнение еще раз: \(C=d\timesπ\). Другими словами, мы можем обернуть нить (длина которой равна диаметру) вокруг круга 3,1415926… раз.

Q

Как мы используем длину окружности в повседневной жизни?

A

Применение окружности в повседневной жизни поистине безгранично! Однако одним из примеров является определение размера шины, необходимой для велосипеда или автомобиля. Другим примером может быть определение количества древесины в дереве: для очень-очень старого дерева было бы довольно сложно измерить диаметр основания дерева; но было бы просто обернуть веревку вокруг основания и измерить окружность. Затем вы можете использовать это измерение окружности и «реконструировать» уравнение окружности, чтобы определить диаметр дерева. С помощью этого измерения (и высоты дерева) мы могли бы найти объем древесины внутри этого дерева. Опять же, список примеров можно продолжать бесконечно, поэтому следите за другими способами использования окружности на протяжении всей своей жизни!

Q

Что такое окружность и диаметр?

A

Окружность — это длина одного полного «круга» вокруг окружности, а диаметр — это длина отрезка, который делит окружность пополам. Думайте об окружности как о внешнем измерении, а о диаметре — как о внутреннем измерении круга!

Q

Является ли диаметр половиной длины окружности?

А

Нет! Помните, что уравнение \(C=2πr\) можно переписать так: \(C=2r\timesπ\), \(C=d\timesπ\) или \(C=d\). Итак, возможно, мы могли бы сказать, что диаметр равен 3,14159.26… ^й окружности…

Q

Является ли диаметр длиной?

A

Если длина определяется как расстояние между двумя точками, тогда да, диаметр является длиной. Диаметр окружности измеряет расстояние между двумя самыми дальними точками окружности.

Практические вопросы

Вопрос №1:

 
Определите длину окружности.

23,16 см

24,14 см

25,12 см

26,11 см

Показать ответ

Ответ:

Длину окружности можно рассчитать по одной из следующих формул: \(C=𝜋d\) или \(C=2)𝜋 .

Мы знаем, что диаметр круга равен 8 см, а приближенное число пи равно 3,14, поэтому мы можем подставить эти значения в формулу \(C=𝜋d\). Формула принимает вид \(C=(3.14)(8)\), что упрощается до 25. 12. Длина окружности 25,12 см.

Скрыть ответ

Вопрос № 2:

 
Определите радиус окружности, если длина окружности составляет двадцать три дюйма. Округлите ответ до сотых.

3,66 дюйма

4,65 дюйма

3,44 дюйма

4,76 дюйма

Показать Ответ

Ответ:

5 Ответ:

5 90 Мы знаем, что длина окружности равна двадцати трем дюймам, поэтому мы можем подставить это значение в формулу \(C=2𝜋r\). Мы также знаем, что приблизительное число пи равно 3,14, поэтому единственное неизвестное нам значение — это 9.0013 р , радиус. Когда C и 𝜋 подставляются в формулу, получается \(23=2(3.14)r\). Это можно упростить до \(23=6,28r\), а затем обе части уравнения можно разделить на 6,28, чтобы выделить переменную r . 23 разделить на 6,28 равно 3,66 при округлении до сотых. Радиус круга равен 3,66 дюйма.

Скрыть ответ

Вопрос № 3:

 
Если C представляет длину окружности, r представляет радиус, а d представляет диаметр, какая формула неверна?

\(d=2r\)

\(C=𝜋d\)

\(C=2𝜋r\)

\(r=𝜋dC\)

Показать ответ