ГОСТ 23597-79 Станки металлорежущие с числовым программным управлением
ОБОЗНАЧЕНИЕ ОСЕЙ КООРДИНАТ И НАПРАВЛЕНИЙ ДВИЖЕНИЙ.
ОБЩИЕ
ПОЛОЖЕНИЯ ГОСТ 23597-79 (СТ СЭВ 3135-81)
Дата введения 01.07 80
Настоящий стандарт распространяется на металлорежущие станки с числовым программным управлением (ЧПУ) и устанавливает обозначение осей координат и направлений движений рабочих органов станка, связанных с обрабатываемой заготовкой (далее — заготовкой) и инструментом.
Стандарт может быть использован для других видов оборудования с ЧПУ
Стандарт полностью соответствует СТ СЭВ 3135—81.
Стандарт полностью соответствует международному стандарту ИСО 841—74.
(Измененная редакция, Изм. № 1, 2).
1. ОБОЗНАЧЕНИЕ НАПРАВЛЕНИЙ ДВИЖЕНИЙ В СТАНКАХ В СТАНДАРТНОЙ СИСТЕМЕ КООРДИНАТ
1.1.
Стандарт устанавливает обозначение осей координат и
направление движений в станках так, чтобы программирование операций обработки
не зависело от того, перемещается инструмент или заготовка.
За основу принимается перемещение инструмента относительно системы координат неподвижной заготовки.
1.2.
Стандартная система координат представляет собой правую
прямоугольную систему координат (см. чертеж), связанную с заготовкой, оси которой параллельны прямолинейным направляющим станка.
Правая прямоугольная система координат
1.3. Положительное направление движения рабочего органа станка предпочтительно соответствует направлению отвода инструмента от заготовки.
1.4. При применении станка для сверления или растачивания, с использованием только трех основных линейных перемещений, обработка будет происходить при перемещении инструмента в отрицательном направлении оси Z.
1.5. На схематических
чертежах станков направления движения рабочих органов, несущих инструмент,
следует обозначать, буквами без штриха, а несущих заготовку — буквами со
штрихом; при этом положительное направление движения, обозначаемое буквой со
штрихом, противоположно соответствующему движению, обозначаемому той же буквой
без штриха.
2. ДВИЖЕНИЕ ПО ОСИ Z
2.1. Ось Z (за исключением случая, указанного в п. 2.5.) определяется по отношению к шпинделю главного движения, то есть шпинделя, вращающего инструмент в станках сверлильно-фрезерно-расточной группы или шпинделя, вращающего заготовку в станках токарной группы.
2.2. При наличии нескольких шпинделей следует выбрать один из них в качестве основного, предпочтительно перпендикулярный к рабочей поверхности стола, на котором крепится заготовка.
2.3. При неповоротной оси основного шпинделя одну из трех осей стандартной трехкоординатной системы, параллельную оси шпинделя, следует принять за ось Z.
2.4. В тех случаях, когда ось основного шпинделя может быть повернута, следует:
если она может находиться только в одном положении параллельно одной из осей стандартной трехкоординатной системы — эту стандартную ось принимают за ось z
если она может
находиться в нескольких положениях, параллельных различным осям стандартной
трехкоординатной системы, за ось Z принимают стандартную ось, предпочтительно
перпендикулярную к рабочей поверхности стола, на котором крепится заготовка.
2.5. При отсутствии шпинделя в станке ось z. должна быть предпочтительно перпендикулярна к рабочей поверхности стола.
2.6. Движение по оси Z в положительном направлении должно соответствовать направлению отвода инструмента от заготовки.
3. ДВИЖЕНИЕ ПО ОСИ X
3.1. Ось X должна быть расположена предпочтительно горизонтально и параллельно поверхности крепления заготовки.
3.2. На станках с невращающимся инструментом и заготовкой, например, строгальных, ось X должна быть положительна в направлении главного движения и параллельна ему.
3.3.
На станках с вращающейся заготовкой, например, токарных,
движение по оси X направлено по радиусу заготовки и параллельно поперечным
направляющим. Положительное движение по оси X происходит, когда инструмент,
установленный на главном резцедержателе поперечных салазок, отходит от оси
вращения заготовки.
3.4. На станках с вращающимся инструментом, например, фрезерных, сверлильных:
при горизонтальной оси Z положительное перемещение X направлено вправо, если смотреть от основного инструментального шпинделя к изделию;
при вертикальной оси z положительное перемещение по оси X направлено вправо для одностоечных станков, если смотреть от основного инструментального шпинделя на стойку, а для двухстоечных станков, если смотреть от основного инструментального шпинделя на левую стойку.
4. ДВИЖЕНИЕ ПО ОСИ Y
4.1. Положительное направление движения по оси Y следует выбирать так, чтобы ось Y вместе с осями Z и X образовывала правую прямоугольную систему координат (см. чертеж).
5. ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ А. В и С
5.1. Буквами А, В и С следует обозначать вращательные движения вокруг осей параллельных соответственно X, Y и Z.
5.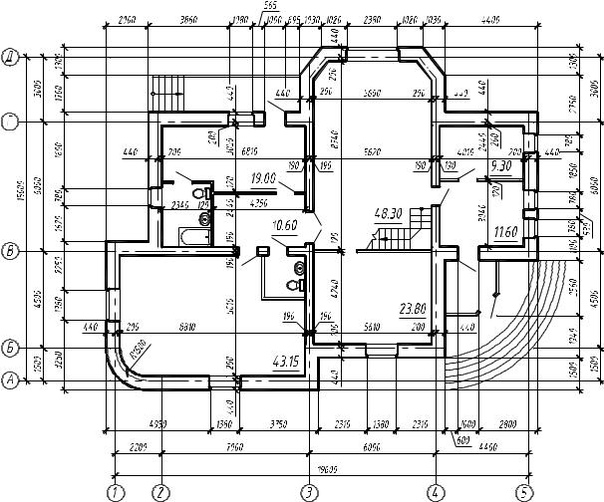 2.
Положительные направления А. В и С должны совпадать с
направлением завинчивания винтов с правой резьбой в положительных направлениях
осей соответственно X, Y и Z (см чертеж).
2.
Положительные направления А. В и С должны совпадать с
направлением завинчивания винтов с правой резьбой в положительных направлениях
осей соответственно X, Y и Z (см чертеж).
6. НАЧАЛО СТАНДАРТНОЙ СИСТЕМЫ КООРДИНАТ
6.1. Расположение начала стандартной системы координат (Х=0, У=О, Z=0) следует выбирать произвольно.
6.2. Начало отсчета движений А, В и С следует выбирать произвольно.
7. ДОПОЛНИТЕЛЬНЫЕ ОСИ
7.1. Прямолинейное движение
7.1.1. Если дополнительно к основным (первичным) прямолинейным движениям X, Y и Z имеются вторичные движения параллельно им, их следует обозначать соответственно U, V и W.
Если дополнительно имеются третичные движения, параллельные им, их следует обозначать соответственно P. Q и R.
Если дополнительно
имеются прямолинейные движения, которые не параллельны или могут быть не
параллельны X, Y или Z, их следует обозначить по выбору U, V, W, Р, Q или R.
Примечание. Для горизонтально-расточного станка движение ползушки радиального суппорта следует обозначать буквами U или Р, если эти буквы не заняты при обозначенном перемещении стола X, так как в этом случав движение резца, хотя и близкое к шпиндели», является наклонным.
7.1.2. Первичные, вторичные и третичные движения рабочих органов станка определяются предпочтительно в соответствии с удаленностью этих органов от основного шпинделя.
Примечания:
а) Для радиально-сверлильного станка движение гильзы шпинделя н траверсы следует обозначать соответственно буквами z и w
б) Для токарно-револьверного станка движения резцовых салазок к салазок револьверной головка», расположенных дальше от шпинделя, следует обозначать соответственно буквами Z и w.
в)
Для станков с двумя функционально одинаковыми рабочими
органами, управляемыми от двух независимых двухкоординатных устройств ЧПУ (например,
для токарных станков с функционально одинаковыми двумя шпинделями и суппортами)
оси координат для обоих одинаково работающих органов (например, суппортов)
следует обозначать одинаково —буквами z и X.
7.2. Вращательное движение
Если дополнительно к первичным вращательным движениям имеются вторичные вращательные движения, параллельные или непараллельные А, В и С. их следует обозначать D и Е.
7.3. Примеры обозначений основных и дополнительных осей координат и положительных направлений движений в металлорежущих станках с ЧПУ приведены в справочном приложении к настоящему стандарту.
ПРИМЕРЫ
ОБОЗНАЧЕНИИ ОСЕЙ КООРДИНАТ И ПОЛОЖИТЕЛЬНЫХ НАПРАВЛЕНИЯ ДВИЖЕНИЙ В МЕТАЛЛОРЕЖУЩИХ СТАНКАХ С ЧПУ
Черт. 1 Токарно-винторезный станок
Черт. 2 Токарно-револьверный станок
Черт.
3 Лоботокарный станок
Черт 4
Токарно-карусельный станок
Черт. 5 Горизонтально-расточной станок с неподвижной передней
стойкой и крестовым столом
5 Горизонтально-расточной станок с неподвижной передней
стойкой и крестовым столом
Черт. 5а Горизонтально-расточной станок с неподвижной стойкой и крестовым поворотным столом
Черт. 6 Горизонтально-расточной станок с продольно-подвижной передней стойкой и поперечно-подвижным поворотным столом
Черт. 6а. Горизонтально-расточной станок с продольно- и поперечно-подвижной стойкой
Черт. 7 Консольно-фрезерный горизонтальный станок
Черт. 8 Консольно-фрезерный вертикальный станок
Черт. 9 Продольно-фрезерный вертикальный станок
Черт.
10 Продольно-фрезерный двухстоечный станок
Черт. 11 Продольно-фрезерный станок с подвижным порталом
Черт. 12 Одностоечный продольно-строганый станок
Черт. 13. Поперечно-строгальный станок
Черт. 14 Круглошлифовальный станок
14 Круглошлифовальный станок
Черт. 15 Плоскошлифовальный станок с горизонтальным шпинделем
Черт. 16 Заточной станок
Chp 02-01 Программирование ЧПУ
Chp 02-01 Программирование ЧПУ Изучение программирования ЧПУ часто превращается в приключение, связанное с перемещением из одного места в другое; хорошо Программирование ЧПУ — это просто упражнение по целенаправленному перемещению из одного места в другое. Но, конечно, как говорит персонаж Бакару Банзай: «Куда бы вы ни пошли, вы там». Для вымышленных нейрохирургов, водителей реактивных автомобилей и рок-н-роллеров это все хорошо. Однако для точной обработки программист должен быть немного более точным… как правило, по крайней мере до четырех знаков после запятой для большинства контроллеров ЧПУ. Чтобы добиться такой точности, программист должен иметь известную систему отсчета в трехмерном (3D) пространстве для каждого движения. Таким образом, при каждом программном перемещении машина будет двигаться (а) по одной или нескольким осям (б) в каком-то направлении (в) к определенному месту назначения и (г) затем что-то делать (как правило, куда-то еще). .
Таким образом, при каждом программном перемещении машина будет двигаться (а) по одной или нескольким осям (б) в каком-то направлении (в) к определенному месту назначения и (г) затем что-то делать (как правило, куда-то еще). .
Какая ось какая?
Движение фрезы ЧПУ может производиться по любой из трех осей, все из которых взаимно перпендикулярны, то есть находятся точно под прямым углом друг к другу. Эти оси движения обозначены буквами X, Y и Z, такими же, как в знакомой нам декартовой системе координат. Направление движения по этим трем осям — вправо и влево, внутрь и наружу, вверх и вниз — обозначается знаком плюс или минус. Большинство станков с ЧПУ предполагают движение в положительном (плюсовом) направлении, если вы не укажете отрицательное направление с помощью знака минус. Направление или условие принимается за станком с ЧПУ, когда не задано конкретное направление, называется состоянием по умолчанию .
Ось Z Какая ось зависит от ориентации шпинделя. Ось движения, параллельная оси шпинделя, всегда является осью Z. Если шпиндель расположен вертикально (рис. 2.1), ось Z вертикальна. Либо пиноль, либо колено фрезерного станка с вертикальным шпинделем будут двигаться при выполнении команды оси Z. Если шпиндель расположен горизонтально, седло или пиноль на фрезерном станке (рис. 2.2) или каретка или револьверная головка на токарном станке (рис. 2.3) будут двигаться параллельно оси шпинделя при выполнении команды оси Z.
Ось движения, параллельная оси шпинделя, всегда является осью Z. Если шпиндель расположен вертикально (рис. 2.1), ось Z вертикальна. Либо пиноль, либо колено фрезерного станка с вертикальным шпинделем будут двигаться при выполнении команды оси Z. Если шпиндель расположен горизонтально, седло или пиноль на фрезерном станке (рис. 2.2) или каретка или револьверная головка на токарном станке (рис. 2.3) будут двигаться параллельно оси шпинделя при выполнении команды оси Z.
Ось X Ось фрезерного станка, которая перемещается вправо и влево (поскольку оператор смотрит перед фрезерным станком), является осью X как для вертикального, так и для горизонтального шпинделя. Для токарных станков ось X представляет собой движение поперечного суппорта (или револьверной головки) под прямым углом к оси шпинделя.
Ось Y Ось Y на фрезерных станках представляет собой либо движение внутрь и наружу — к оператору и от него (вертикальный шпиндель), либо движение вверх и вниз (горизонтальный шпиндель).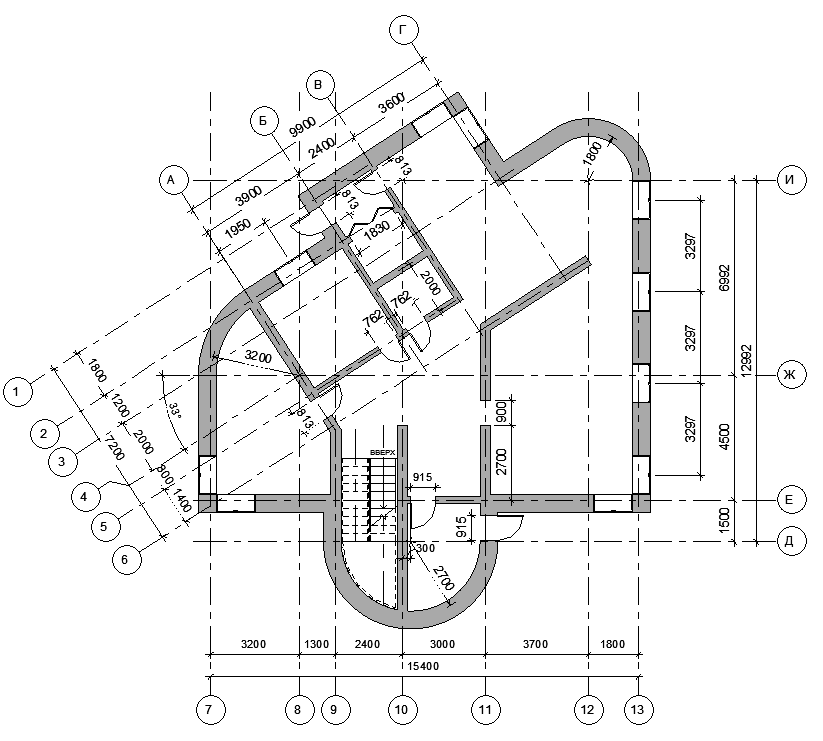 Простые токарные станки с ЧПУ являются двухосевыми станками и не имеют оси Y.
Простые токарные станки с ЧПУ являются двухосевыми станками и не имеют оси Y.
Следует отметить, что сложные многошпиндельные токарные обрабатывающие центры или швейцарские винтовые станки с несколькими автоматическими патронами, оснащенные так называемым «подвижным инструментом», могут иметь одну из двух осей Y.
Какое направление какое?
Положительные направления движения фрезы для вертикально-шпиндельного фрезерного станка: справа от оператора (ось X), от оператора (ось Y) и вверх (ось Z).
Станки с ЧПУ с горизонтальным шпинделем немного более запутаны. Для ощущения направления нужно смотреть в направлении Z-минус, как если бы ваш глаз застрял в шпинделе и смотрел на заготовку. Тогда положительные направления движения режущего инструмента: вправо (ось X), вверх (ось Y) и к концу шпинделя (ось Z).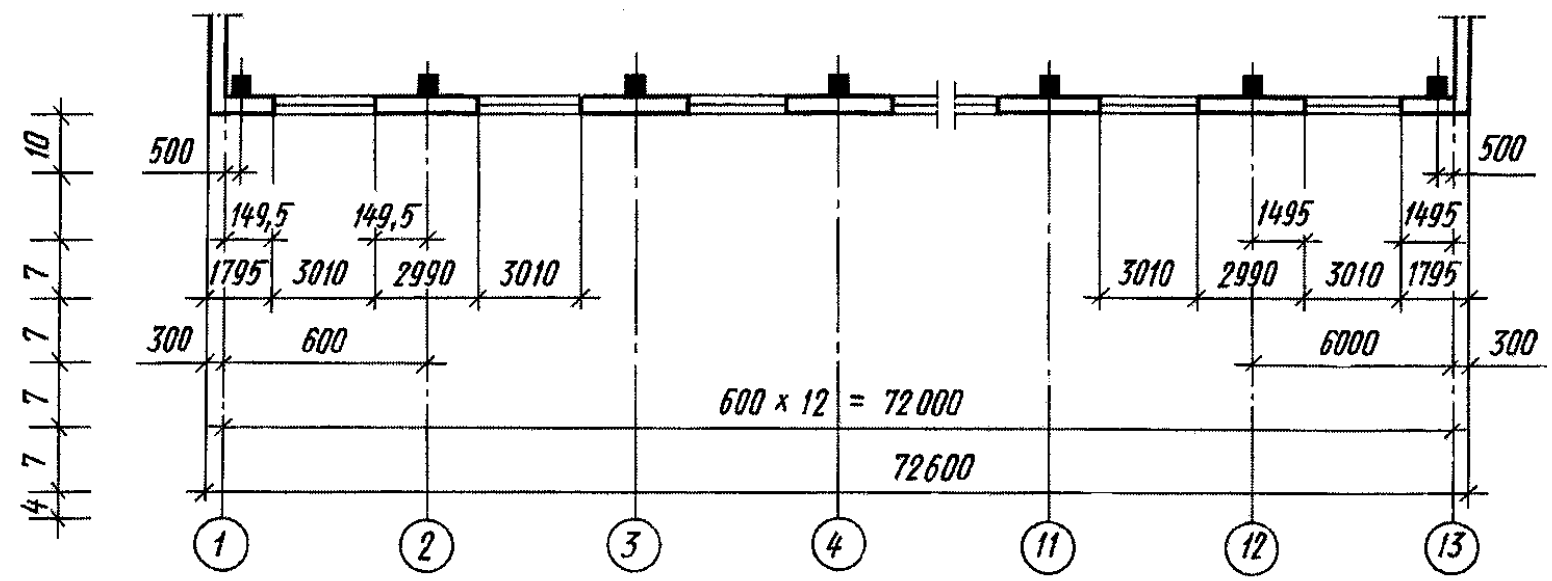
Для токарных станков с ЧПУ положительное направление движения режущего инструмента — от передней бабки, обычно вправо (ось Z), и от оси шпинделя (ось X). Для станков с задним расположением инструмента направление X-plus от оператора. Для станков с передним расположением инструмента направление X-plus направлено к оператору.
Определение точки режущего инструмента
Программисту не нужно сообщать контроллеру ЧПУ, где находится резак. Контроллер всегда отслеживает текущее положение точки режущего инструмента (центр фрезы, на кончике) относительно контрольной точки, называемой исходной точкой.
Происхождение — это точка, из которой исходят все три оси. Иными словами, начало координат — это положение точки режущего инструмента, когда все счетчики трех осей имеют нулевое значение (X0, Y0, Z0). Таким образом, это «нулевая точка», от которой либо (1) отсчитываются все точки координат фрезы ( абсолютное позиционирование) или (2) точка, с которой фреза начинает (и заканчивает) в начале (и конце) программы ( инкрементальное позиционирование).
Исходной точкой обычно является точка, положение которой определяется программистом. Некоторые старые станки с ЧПУ имеют исходную точку с предварительно заданным фиксированным положением в пределах диапазона перемещения станка (обычно на поверхности стола в его нижнем левом углу). Для токарного станка начало координат может быть задано на оси шпинделя и на конце носика шпинделя.
Чаще всего это место, где оси – или, точнее, точка режущего инструмента – могут быть расположены, когда определенная кнопка на панели управления нажата, что “обнуляет” счетчики осей в контроллере.
Программист предполагает, что в начале программы фреза находится в определенной начальной точке заготовки, например, в левом верхнем углу или в центре, при этом конец фрезы «касается» верхней части заготовки. заготовка. Все, что должен сделать оператор ЧПУ при настройке, — это «переместить» резак в это место и нажать кнопку «ZERO AXES», чтобы сместить или «переместить» начало координат в это место. Этот тип называется с плавающим нулем станок с ЧПУ.
Этот тип называется с плавающим нулем станок с ЧПУ.
Абсолютное и инкрементное позиционирование
Некоторые контроллеры ЧПУ могут принимать только команды абсолютного позиционирования, в то время как другие могут принимать только команды инкрементного позиционирования. Более новые контроллеры станков с ЧПУ могут принимать как абсолютные, так и инкрементальные команды позиционирования. Все, что нужно сделать программисту, это сообщить контроллеру (посредством кода), являются ли команды позиционирования абсолютными или инкрементными. Таким образом, программист может переключаться с абсолютного на инкрементное позиционирование так часто, как пожелает, путем изменения кода.
Абсолютное позиционирование
Абсолютное позиционирование всегда сообщает контроллеру, куда направить фрезу относительно
origin (а не текущее положение точки режущего инструмента). Контроллер всегда знает, где в данный момент находится резак, поэтому он может рассчитать расстояние и направление, в котором он должен отправить резак, чтобы добраться до нужного пункта назначения.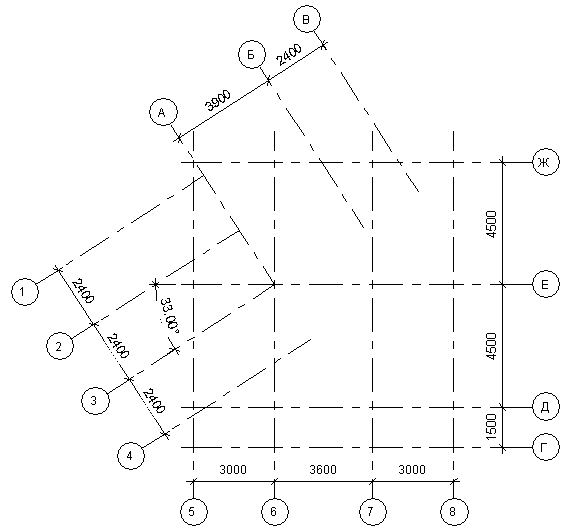
На рисунках 2.4 и 2.5 показаны концепции инкрементного и абсолютного измерения. Эти концепции определения размеров аналогичны инкрементному и абсолютному позиционированию, используемому в ЧПУ.
Инкрементальное позиционирование
Инкрементальное позиционирование всегда сообщает контроллеру, куда направить фрезу относительно текущего местоположения фрезы .
Таким образом, для пошагового позиционирования необходимо в конце программы, чтобы фреза оказалась точно в том же месте, откуда она вышла в начале программы. Начальная и конечная точки должны быть равны 9.0004 идентичен . Это можно сформулировать математически: алгебраическая сумма всех перемещений осей в инкрементальной программе должна равняться нулю:
Если исходная точка “смещается” с каждой последующей заготовкой, появляется ошибка, которая становится все больше с каждой последующей заготовкой. Это называется «прогрессивной ошибкой».
Это называется «прогрессивной ошибкой».
| Далее: N/C форматы и грамматика |
|---|
Назад на страницу содержания
Обновлено 9 января 2002 г.
Авторские права 1988-2002 принадлежат Джорджу Стэнтону и
Билл Хемфилл
Все права защищены
Станок с ЧПУ Программируемые оси и системы измерения положения – Производственные процессы 4-5
После завершения этого раздела вы должны уметь:
- Понимать декартову систему координат.
- Знать декартовы координаты плоскости.
- Знать декартовы координаты трехмерного пространства.
- Поймите четыре квадранта.
- Объясните разницу между полярной и прямоугольной координатами.
- Определите программируемые оси на станке с ЧПУ.
Декартовы координаты позволяют задать положение точки на плоскости или в трехмерном пространстве. Декартовы координаты или прямоугольная система координат точки представляют собой пару чисел (в двух измерениях) или тройку чисел (в трех измерениях), которые задают расстояния со знаком от оси координат. Сначала мы должны понять систему координат, чтобы определить наши направления и относительное положение. Система, используемая для определения точек в пространстве путем установления направления (оси) и опорного положения (начала). Система координат может быть прямоугольной или полярной.
Декартовы координаты или прямоугольная система координат точки представляют собой пару чисел (в двух измерениях) или тройку чисел (в трех измерениях), которые задают расстояния со знаком от оси координат. Сначала мы должны понять систему координат, чтобы определить наши направления и относительное положение. Система, используемая для определения точек в пространстве путем установления направления (оси) и опорного положения (начала). Система координат может быть прямоугольной или полярной.
Точно так же, как точки на прямой можно поставить в однозначное соответствие с линией действительных чисел, так и точки на плоскости можно поставить в однозначное соответствие с парами строк действительных чисел, используя две координатные линии. Для этого построим две перпендикулярные координатные линии, пересекающиеся в своих началах; для удобства. Назначьте набор равновеликих делений для осей x и y, начиная с начала координат и идущих в обоих направлениях, влево и вправо (ось x) и вверх и вниз (ось y) точки вдоль каждой оси.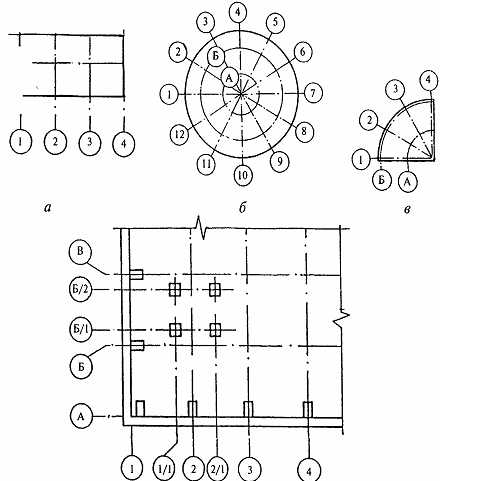 Мы делаем одну из числовых линий вертикальной с положительным направлением вверх и отрицательным направлением вниз. Другие числовые линии горизонтальны с положительным направлением вправо и отрицательным направлением влево. Две числовые линии называются осями координат; горизонтальная линия — это ось x, вертикальная линия — это ось y, а оси координат вместе образуют декартову систему координат или прямоугольную систему координат. Точка пересечения осей координат обозначается буквой О и является началом системы координат. См. рис. 1.
Мы делаем одну из числовых линий вертикальной с положительным направлением вверх и отрицательным направлением вниз. Другие числовые линии горизонтальны с положительным направлением вправо и отрицательным направлением влево. Две числовые линии называются осями координат; горизонтальная линия — это ось x, вертикальная линия — это ось y, а оси координат вместе образуют декартову систему координат или прямоугольную систему координат. Точка пересечения осей координат обозначается буквой О и является началом системы координат. См. рис. 1.
Рисунок 1
По сути, это две линии действительных чисел, соединенные вместе, одна из которых идет влево-вправо, а другая — вверх-вниз. Горизонтальная линия называется осью x, а вертикальная линия называется осью y.
Точке (0,0) дается специальное имя «Начало», иногда ей присваивается буква «О».
Основой этой системы является числовая линия, размеченная через равные промежутки. Ось помечена (X, Y или Z). Одна точка на линии обозначается как начало координат. Числа на одной стороне линии отмечены как положительные, а числа на другой стороне отмечены как отрицательные. См. рис. 2.
Числа на одной стороне линии отмечены как положительные, а числа на другой стороне отмечены как отрицательные. См. рис. 2.
Рис. 2. Числовая линия оси X
Плоскость, в которой введена прямоугольная система координат, является координатной плоскостью или плоскостью x-y. Теперь мы покажем, как установить однозначное соответствие между точками на координатной плоскости и парами действительных чисел. Если А — точка на координатной плоскости, то через А мы проводим две линии, одну перпендикулярную оси х, а другую — перпендикулярную оси у. Если первая линия пересекает ось x в точке с координатой x, а вторая линия пересекает ось y в точке с координатой y, то мы связываем пару (x, y) с A (см. рисунок 2). Число a является координатой x или абсциссой P, а число b является координатой y или ординатой p; мы говорим, что A является точкой с координатой (x, y) и обозначаем точку через A (x, y). Точке (0,0) дается специальное название «Начало», а иногда ей присваивается буква «О».
Абсцисса и ордината:
Слова «Абсцисса» и «Ордината»… это просто xandyvalues:
- Абсцисса: значение по горизонтали («x») в паре координат: насколько далеко расположена точка.

- Ордината: значение по вертикали («y») в паре координат: насколько далеко вверх или вниз находится точка.
Рисунок 3
Отрицательные значения X и Y:
Строка действительных чисел, вы также можете иметь отрицательные значения.
Отрицательный: начать с нуля и двигаться в противоположном направлении; См. рис. 4
Рисунок 4
Итак, для отрицательного числа:
- goleftfor x
- godownfor
Например, (-3,5) означает:
идти влево по оси x 3, затем вверх на 5 по оси y. (Квадрант II x отрицательный, y положительный)
И(-3,-5)означает:
идти влево по оси х 3, затем идти вниз 5 по оси у. (Квадрант III x отрицательный, y отрицательный)
Используя декартовы координаты, отметьте точку на графике, как далеко вдоль и как высоко она находится; См. рисунок 5. Точка (12,5) находится на расстоянии 12 единиц по оси x и на 5 единиц вверх по оси y.
Рисунок 5
Ось X и Y:
Горизонтальная линия называется осью X, а вертикальная линия называется осью Y; обе строки проходят через ноль(Origin, (0,0)).
Горизонтальная линия называется осью X, а вертикальная линия называется осью Y; обе строки проходят через ноль(Origin, (0,0)).
Соедините их на графике … См. рис. 6
Рисунок 6
По сути, это набор из двух строк с действительными числами.
Ось: Базовая линия, от которой измеряются расстояния.
Пример:
Точка(6,4) равна
Пройдите по оси x 6 единиц, затем поднимитесь на 4 единицы вверх в их направлении, затем «поставьте точку».
А запомнить какая ось какая по:
Координаты всегда записываются в определенном порядке:
- горизонтальное расстояние сначала,
- , затем расстояние по вертикали.
Заказанная пара:
Числа разделены запятой, и все это заключено в круглые скобки следующим образом: (7,4)
Пример: (7,4) означает 7 единиц вправо (ось X) и 4 единицы вверх (ось Y)
В трехмерном пространстве (пространстве xyz), ориентированном под прямым углом к плоскости xy. Ось z проходит через начало координат плоскости xy. Координаты определяются по направлениям восток-запад по оси x, север-юг по оси y и смещения вверх-вниз по оси z от начала координат. Декартова система координат основана на трех взаимно перпендикулярных координатных осях: ось х, ось они и ось z, см. рис. 6 ниже. Три оси пересекаются в точке, называемой началом координат. Вы можете представить себе начало координат в точке, где стены в углу комнаты встречаются с полом. Ось x — это горизонтальная линия, вдоль которой пересекаются стена слева от пола. Их-ось — это горизонтальная линия, по которой пересекаются стена справа от вас и пол. Ось z — это вертикальная линия, по которой пересекаются стены. Части линий, которые вы видите, стоя в комнате, являются положительной частью каждой из осей. Отрицательной частью этих осей будут продолжения линий за пределами комнаты.
Ось z проходит через начало координат плоскости xy. Координаты определяются по направлениям восток-запад по оси x, север-юг по оси y и смещения вверх-вниз по оси z от начала координат. Декартова система координат основана на трех взаимно перпендикулярных координатных осях: ось х, ось они и ось z, см. рис. 6 ниже. Три оси пересекаются в точке, называемой началом координат. Вы можете представить себе начало координат в точке, где стены в углу комнаты встречаются с полом. Ось x — это горизонтальная линия, вдоль которой пересекаются стена слева от пола. Их-ось — это горизонтальная линия, по которой пересекаются стена справа от вас и пол. Ось z — это вертикальная линия, по которой пересекаются стены. Части линий, которые вы видите, стоя в комнате, являются положительной частью каждой из осей. Отрицательной частью этих осей будут продолжения линий за пределами комнаты.
Рис. 7. Трехмерная декартова система координат
Трехмерные декартовы координатные оси. Представление трех осей трехмерной декартовой системы координат. Положительная ось x, положительная ось y и положительная ось z — это стороны, обозначенные x, y и z. Начало — это пересечение всех осей. Ветвь каждой оси на противоположной стороне от начала координат (немаркированная сторона) является отрицательной частью.
Положительная ось x, положительная ось y и положительная ось z — это стороны, обозначенные x, y и z. Начало — это пересечение всех осей. Ветвь каждой оси на противоположной стороне от начала координат (немаркированная сторона) является отрицательной частью.
При работе с трехмерным движением необходимо настроить подходящую систему координат. Наиболее простой тип системы координат называется декартовой системой. Декартова система координат состоит из трех взаимно перпендикулярных осей, осей X, Y и Z. По соглашению ориентация этих осей такова, что, когда указательный, средний и большой пальцы правой руки расположены взаимно перпендикулярно, указательный, средний и большой пальцы могут быть взаимно перпендикулярны. выровнены по осям X, Y и Z соответственно. Такая система координат называется правой. См. рис. 7. Точка пересечения трех осей координат называется началом системы координат.
Рис. 8. Правосторонняя декартова система
Декартовы координаты точки в трех измерениях представляют собой тройку чисел (x,y,z). Три числа или координаты определяют расстояние со знаком от начала координат по осям x, y и z соответственно. Их можно визуализировать, сформировав прямоугольник с ребрами, параллельными оси координат и противоположными углами в начале координат и заданной точке.
Три числа или координаты определяют расстояние со знаком от начала координат по осям x, y и z соответственно. Их можно визуализировать, сформировав прямоугольник с ребрами, параллельными оси координат и противоположными углами в начале координат и заданной точке.
Теперь точки могут быть определены в трехмерном объеме пространства. Это позволяет определять точки в трех измерениях от начала координат. Декартовы координаты (x, y, z) точки в трех измерениях определяют расстояние со знаком от начала координат по осям x, y и z соответственно. Точки оси Z становятся третьей записью при определении местоположений координат.
Учитывая приведенную выше аналогию с углом комнаты, мы могли бы сформировать декартовы координаты точки на макушке следующим образом. Представьте, что ваш рост составляет пять метров по оси Z, и вы проходите два метра от начала координат по оси X, затем поворачиваете налево и идете параллельно оси Z на четыре метра в комнату. Декартовы координаты точки на макушке вашей головы будут (2,4,5).
Например, обозначение (2,4,5) соответствует значению X2, Y4 и Z5. См. рис. 8.
Декартовы координаты могут использоваться для определения местоположения точек в 3 измерениях, как в этом примере:
Рис. 9. Точка (2, 4, 5) показана в трехмерных декартовых координатах.
Оси координат делят плоскость на четыре части, называемые квадрантами (см. рис. 9). Квадранты пронумерованы против часовой стрелки, начиная с верхнего правого угла, обозначены I, II, III и IV с обозначениями осей, как показано на рисунке ниже.
Рисунок 10
Четыре квадранта:
Когда мы включаем отрицательные значения, оси x и y делят пространство на 4 части:
Квадранты I, II, III и IV
(Пронумерованы против часовой стрелки)
InQuadrant I: и x, и y положительны
InQuadrant II: x неотрицательно (y все еще положительно)
InQuadrant III: и x, и y отрицательные
InQuadrant IV 😡 снова положительный, а y отрицательный
| Квадрант | X (горизонтальный) | Y (вертикальный) | Пример |
| я | Положительный | Положительный | (3,2) |
| II | Отрицательный | Положительный | (-5, 2) |
| III | Отрицательный | Отрицательный | (-2, -1) |
| IV | Положительный | Отрицательный | (2, -5) |
Пример: точка «A» (3,2) находится на расстоянии 3 единиц по оси x и 2 единиц вверх по оси y.